0 引言
电能质量的概念自从提出以来就一直含糊不清,用户方、制造方和供电方对之的理解也大相径庭。早期用户设备对电压扰动不敏感,而且不容易对系统电压与频率造成负面影响,因此用电压和频率的偏移或畸变程度来衡量电能质量的好坏就足够了。近年来,由于以下原因,电能质量问题变得复杂起来:1)电力电子设备和敏感的微处理控制器的使用;2)工业处理过程的复杂化;3)大型计算机的投入;4)用于提高电力系统稳定性的FACTS装置的大量运用;5)高效可调速电动机等电力设备的投切;6)庞大的电网互联结构;7)生产精密设备的要求。因此,传统的电能质量的概念被IEEE第22标准协调委员会推荐采用的11种动态电能质量专用术语[1]取代:断电(Interruptions)、频率偏差(Frequency Deviations)、电压跌落(Sags)、电压上升(Swells)、瞬时脉冲或突波(Transients Surges)、电压波动(Voltage Fluctuations)、电压切痕(Notches)、谐波(Harmonics)、间谐波(Interharmonics)、过电压(Overvoltages)和欠电压(Undervoltages)。随之而来的问题是缺乏对这些暂态现象行之有效的检测分析方法。只有正确识别影响电能质量的诸多因素、查明相应的起因和来源、检测、分类并统计扰动现象、确定扰动范围和幅值才能从根本上综合治理并提高系统电能质量。
为此,国际上以多种形式、用各种方法和技术对电能质量的扰动问题展开了多方面的研究与探讨。综合起来,这些方法可以归为利用各种数学变换、利用各种人工智能技术,以及利用人工智能和数学变换结合的方法对扰动进行检测、分类和抑制。
1 数学变换的应用
1.1 傅立叶变换
影响电能质量的暂态信号通常具有很宽的频谱,将其按频谱展开能揭示故障的本质。傅立叶变换(FT)就是最常见的一种将时域特征和频域特征联系起来的工具。通过傅立叶变换可以提供平稳信号所含谐波的次数、各次谐波的幅值及其初相角并以幅频特性的形式表现出来,因此可以用于提取由于变压器、交直流换流设备等造成的周期性谐波分量[2-4]。FT的缺点是:1)必须获得信号在时域中的全部信息;2)对信号的局部畸变没有标定和度量能力,因此无法充分描述时变非平稳信号的特征; 3)无法反映信号在局部时间范围内和局部频带上的谱信息。
解决的一个办法是短时傅立叶变换(STFT),通过引入一个滑动的时间局部化“窗口函数”,对信号进行分段截取,从而得到信号在某一固定时窗和频窗内的局部时-频信息。选择相对于扰动小的多的时窗(必须仔细选择时窗以避免吉布斯现象),STFT可以很好地反映信号局部范围内的谐波次数及幅值[5-7], 因此适用于检测与谐波相关的扰动。STFT的缺点是:1)没有离散正交基,因此在进行数值计算时没有象FFT这样有效的快速算法;2)一旦选定窗口函数,时-频窗的窗口形状是固定的,所以对非平稳信号的分析能力有限,尽管文献[6]提出用宽时窗和窄时窗分别对信号进行扫描,但仍无法改变STFT单一分辨率的事实。
用Wigner谱分析方法可以克服STFT的上述缺点,它是基于两个信号内积的傅立叶变换,和STFT一样是时-频二维联合分布函数,可以近似看作在时-频二维平面上的能量密度函数。由于它具有较高的分辨率、能量集中性和跟踪瞬时频率的能力,用于进行电能质量分析时,不但可以准确测量基波和谐波分量的幅值,而且能够准确检测到信号发生尖锐变化的时刻[5,8,9]。它的不足在于:1)必须以大于Nyquist采样频率两倍以上的频率进行采样;2)存在严重的交叉干扰现象。
1.2 小波变换
国外最早关于小波变换在电力系统中的应用的文章就是针对电能质量的评估展开的[10]。国内期刊上首次出现这方面的文章介绍则是在1999年[11],而到目前为止,在这方面所开展的工作仍然很少。
1.2.1 扰动的识别
利用小波变换在突变点的特性,可实现对电能质量中的周期性陷波、暂态振荡、电压跌落以及闪变等扰动问题的幅值、发生时间与持续时间等特征参数的判断。1994年,S.Santoso首先在文献[12]提出小波变换是评估电能质量的有效方法。该文用db4和db10小波函数分别对电压跌落、平顶波和谐波畸变进行小波变换,实现了对电能质量扰动的检测与时间定位。但并未讨论小波母函数的选择对检测结果的影响。文献[13]则通过分析比较得出db4小波是db小波系中最适用于检测电能质量扰动的小波的结论。文献[14]还对重构信号和原始信号的误差以及小波分析和傅氏分析的结果进行比较。另外,利用连续小波变换后的时-频相平面图可检测电压跌落和瞬时过电压[15];利用小波变换的模极大值理论[16-18]同样可精确地对电压跌落的发生、恢复时刻进行定位。文献[19]则倾向于对傅氏变换和小波变换下电压下降的三个指标:RMS、最大值和基频幅值进行比较,该文同时还分析了不同时窗选择的重要性。
为了提取暂态信号中各分量的幅值包络、相位、瞬时频率等特征信息,得到比实小波更多的信息,可采用基于小波变换的解析信号分解方法[20],或以复小波为小波母函数[21-22],利用复小波变换的复合信息和相位信息辅助幅值信息进行扰动信息检测。
1.2.2 扰动数据的压缩
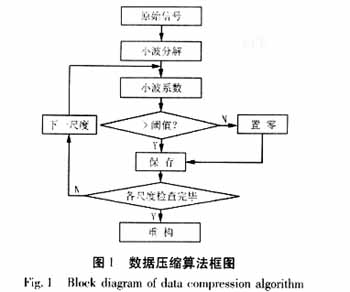
当电力系统发生扰动后,为了记录下完整的扰动信息,通常需要1~4MHz的采样率,使得数据量极大。如此庞大的数据量向调度中心上传时,不但占用数据通道时间过长而且容易造成数据通道阻塞。这使电磁暂态信号的数据存储和数据通信均面临如何提取暂态信号中的有效部分,实现数据压缩的挑战。电力系统中现有扰动监测仪的数据简约技术采用重叠方法即对现有数据不断覆盖,或采用量化技术即把一系列相同的波形看成一个整体[23]。这两种方法的确节省了存储空间,但却不是一般意义上的数据压缩概念。利用小波变换分解和重构的特性对电压扰动数据进行压缩[24-27]的算法见图1。该方法首先定一个阈值,然后将绝对值小于阈值的信号的小波变换系数置为零,仅仅将非零系数的位置及 其数值记录下来。这种方法的压缩比主要决定于非零系数的多少,一般压缩后的数据长度只有原信号的1/6-1/3,相应的压缩率可达到3-6倍。将压缩后的信号重构所得到的恢复信号与原始信号的归一化均方误差小于10-6-10-5。这样经过压缩既节省了录波器内存又节约信道,且压缩造成的失真小。
1.2.3 扰动的分类
文献[28]是最早以文章的形式发表的运用小波理论对扰动进行分类的文章。该文运用一非正交的二次样条小波将暂态波形进行小波变换,提取变换后的特征信号,然后运用贝叶斯分类器来识别各种暂态。但此方法的实现过程却太过繁琐。文献[29-30]考虑用最大似然法来进行扰动的分类。文献[29]首先设计了一个滤波器把扰动分量从基频分量中提取出来,之后用Battle-Lemarie样条小波函数对扰动分量进行小波变换,将得到的小波系数进行特征提取后,用最大似然准则得到最终决策。该方法不但可以区分各种电压扰动且能指出扰动的原因。文献[30]使用基于小波的隐Markov模型的参数最优化估计方法,正确率可达到95.5%。文献[31]进一步改进了文献[30],提出在时域内基于规则,而在频域内基于隐Markov模型的扰动分类方法。文献[32]则利用扰动信号在不同尺度下的能量分布的不同,建造了一条基于多分辨率的扰动偏差曲线,根据不同扰动在此曲线上呈现出的差别,此方法不但能有效地检测各种扰动,还能对扰动原因进行判断。文献[33]提出在时域而非频域内确定扰动的起始时刻和持续时间,用一基于Vetterli-Herley-Sweldens定理的Lifting方法构成的双正交复小波,在小波域内一个特定尺度下确定幅度,之后用二进数特征量表示不同扰动,进行分类。该文对五种暂态扰动进行分类,结果正确。
但是,由于电能质量扰动涉及的特征量太多,使得分类判据复杂易错,因此直接提取小波变换后的特征量进行扰动分类的研究并不是太多。大量的电力工作者转为研究用人工智能的方法对扰动进行分类。
2 人工智能的应用
近年来,人工智能技术发展迅速,分支众多,除了人工神经网络、模糊逻辑、专家系统和遗传算法等技术,也有人研究将不同特性的智能技术结合起来进行应用,如:模糊神经网络、小波神经网络、模糊专家系统、自适应模糊逻辑等,以期对电力系统的运行、监试、预测、控制和规划发挥更大的作用。
2.1 扰动的分类
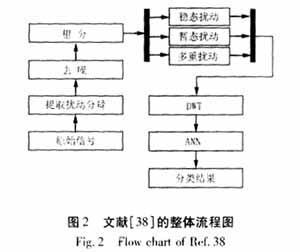
早期的利用ANN对扰动进行分类的方法直接用DFT提取信号中的不同谐波次数,并且把若干次谐波次数归为一类扰动的特征量(3次、6次和9次谐波作为一种,5次和7次谐波作为一种,11次和13次谐波作为一种)输入不同的神经网络[34]进行分类。由于受DFT的限制,这种方法的有效性受到限制,但这种思路却一直延续至今。1996年,S.Santoso在文献[35]中将双正交小波用于检测、定位和识别不同原因的电能质量扰动问题。作者认为可以根据在各尺度下小波系数平方值体现出的特征,用ANN等软计算方法对电能质量的扰动进行自动识别。该文献对将小波变换应用于电能质量的评估做了探索性的研究和有益的尝试,但并未讨论由于输入数据的误差所带来的分类器判断错误的问题。同年,文献[36]采用非正交样条小波重又对电容器投切暂态进行分析,该文作者对文献[28]中未讨论的具体实现细节进行了大量的工作。首先利用滤波器组给出了一个可用任何小波进行变换的数字设备,然后利用与文献[35]相同的思路对暂态信号进行特征的提取。在S.Santoso思想的启发下,F.Mo [37]提出可以利用ANN技术实现智能暂态录波仪,以克服传统录波仪必须人工分析波形、阈值严格以及无法提供实时信息等缺点。但该文并未提供任何具体的实现步骤。B.Perunicic[38]也提出一种集数字滤波、小波变换和ANN为一体的电能质量检测和分类的新方法。总体思路如图2所示。该文对噪声、次谐波畸变、周期性电压波动、电压凹陷、直流偏移以及振荡等10种电能质量扰动问题进行检测与分类,得到良好的效果。同时,该文对小波母函数的选择、采样率和采样周期、监测器位置和性能等细节问题进行了全面地讨论。
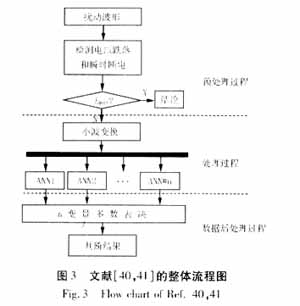
2000年,S.Santoso利用傅氏和小波变换的方法对电能质量扰动进行了特征提取[39]后,提出了完整的基于小波的电能质量扰动波形的神经网络分类器的实现方法[40-41]。这两篇文章对小波理论及其在电力系统中的应用起到了重要的作用,主要流程示于图3。其中Ident表示用传统的方法判断扰动是否为电 压跌落或瞬时断电,之所以不用小波变换处理这两种情况是由于小波变换难以处理光滑连续的电压跌落。 该文提出用各尺度下的小波系数作为ANN的输入特征矢量,这使该工作的输入量太大,于是,文献[42-43]提出用各尺度下的能量的集合作为扰动的特征输入矢量,不但使输入量大为减小,而且得到很好的分类效果。文献[44]则首先找出小波变换后含最大能量的尺度,用该尺度的小波系数与原始正弦波形的小波系数相减,并取其差值作为神经网络的输入变量,从而成功对8种单一扰动进行了有效区分。
但基于小波的ANN方法有时也会误判,而且对多重扰动的分辨率低或者根本无法分辩。这是由于以下原因:1)小波变换难以检测频率微变扰动;2)用来作为ANN输入量的特征量难以选取,无法精确描述各种扰动;3)送入ANN进行训练的样本数无法全面覆盖各种扰动问题;4)基于小波的ANN方法训练的结果受ANN本身结构的限制。
文献[45]对ANN进一步改进,提出使用小波模糊ANN分类器对电能质量问题进行检测与分析,该方法首先从原始信号中提取扰动分量并去噪,然后用小波变换提取特征值,最后进行模糊ANN分析与识别,该方法大大减少了输入ANN的特征值的个数,且对各种扰动问题有良好的适应性。文献[46]提出ANN模糊分类器。该文首先将扰动分为三组,选取不同尺度下的小波系数分别作为这三组的ANN输入特征量,在ANN训练后,再通过一模糊联想记忆变换,最大限度消除模式识别中的不确定性,从而提高系统的精确性并简化模型。文献[47]为电能质量的扰动的分类提供了一条全新的思路。它把模糊逻辑和专家系统结合,通过FFT/WT重新定义了8个特征量,建立相应的规则,也得到了很好的分类效果。
2.2 电能质量的提高
除了用AI方法对电能质量的扰动进行分类分析外,也有文献考虑用AI方法提高电能质量,包括用模糊方法实现电压和无功的控制[48]、用专家系统、遗传算法和模糊集理论实现电容器组的最优分布[49-51];用模糊逻辑分析扰动对敏感负荷的作用[52]。
3 结论
目前,在动态电能质量缺少统一的定义、统一的实践标准和统一的对扰动进行解释的标准的情况下,结合各种人工智能技术和先进的数学变换工具在对动态电能质量进行检测与识别中的作用已成为一个不争的事实。各种AI方法和数学变换均有优点也有缺陷,没有哪一种方法是万能的,应该结合各自的长处,对动态电能质量进行最有效的分析。目前为止,对动态电能质量进行识别使用得最多的仍然是基于小波变换的ANN技术,其它AI方法的研究尚不多见,而且,大部分的识别只针对单一扰动,而对多重扰动的分析几乎没有,这些问题有待进一步的研究。

