文献标识码: A
文章编号: 0258-7998(2011)01-0087-04
短波通信被广泛应用于军事通信领域。但受系统带宽的限制及信道条件的影响,短波通信的传输速率较低。美国Sanders公司推出一种相关跳频电台[1-2]能实现较高的数据传输速率,它以差分跳频为技术核心,有机地将信息调制与跳频控制结合在一起,跳频速率可达到5 000跳/s,增强了系统抗多径及抗干扰能力。在差分跳频系统中,当前一跳的频率值Fn由上一跳的频率值Fn-1以及要发送的数据Xn来决定,其关系式可以表示为:
Fn=G(Fn-1,Xn)
其中G为频率转移函数,它根据所要发送信息数据的不同,在相邻两跳频点间建立一定的关联。G函数的设计直接影响差分跳频系统性能。
在系统接收端,差分跳频系统的信号检测技术是差分跳频系统的一项关键技术,使用的信号检测方法不同,其系统性能也不同[3-4]。如果不考虑前后频点间的相关性,逐符号进行非相干检测及判决,则称这种方法为逐符号检测;如果考虑前后频点间的相关性,利用频点间的对应关系,可对一些错误检测的频率进行纠正,针对一定长度的频率序列采用一定的准则来进行信号的检测与判决,这种方法称为频率序列检测,采用频率序列检测可以提高差分跳频系统性能。维特比算法可以在接收端对频率序列进行检测。传统的序列检测算法多采用线性合并,本文提出差分跳频系统噪声归一化合并接收,将每个频点处的非相干检测值用该频点处的噪声功率进行归一化处理后,再进行维特比译码,可提高差分跳频系统的抗干扰性能。
1 系统模型
假设差分跳频频率集中的跳频点数为N,每跳所传送的比特数为BPH,发送的信号经过非频率选择性慢衰落Rayleigh信道,每跳信号所经历的衰落相互独立,并受到部分频带噪声的干扰。部分频带噪声可建模为零均值的高斯随机过程,其总功率在跳频带宽的一部分ρ,0<ρ<1上均匀分布,其他部分为零。在功率谱密度不为零的范围内,其值为NJ/ρ,NJ为部分频带噪声干扰的等效单边功率谱密度。背景噪声设为零均值、单边功率谱密度为N0的高斯白噪声。因此,当信号受到干扰时,总的噪声功率谱密度为N0+NJ/ρ;当信号未受到干扰时,噪声功率谱密度为N0。
差分跳频系统噪声归一化接收机模型如图1所示。在发送端,数据经G函数进行编码,输出的频率控制字直接控制DDS,从频率集中选择合适的频率进行发送。发送信号经过非频率选择性Rayleigh衰落信道,同时受到部分频带干扰以及加性高斯白噪声的影响,假设收发双方经过严格的同步,则接收信号可以表示为:
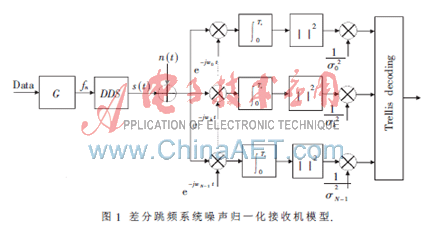

2 性能分析
采用维特比算法进行数据解调时,由于涉及各个频率转移路径间的互相关性,推导准确的符号错误概率非常复杂,因此可参照卷积编码差错概率联合边界的方法,给出差分跳频系统误码率的上边界。差分跳频G函数的状态转移函数为计算首次差错事件概率提供了必要的信息,假设差分跳频系统的状态转移函数为:


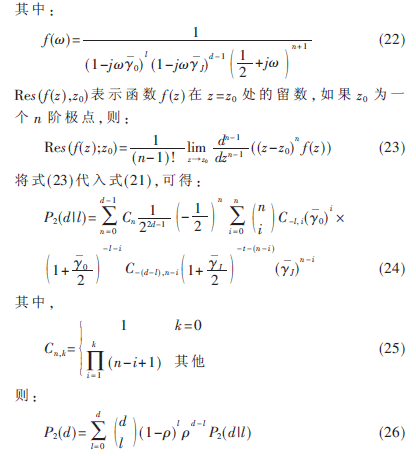
将式(24)、(26)代入式(3)中,即可得到差分跳频系统噪声归一化接收机误码界。
3 仿真结果及分析
为了验证理论误码界推导的正确性,在Rayleigh信道条件下,将理论误码界与仿真结果相比较,由于当跳频系统中的跳率点数过多时,推导G函数的状态转移方程较为复杂,因此,为简单起见,设跳频系统的频点个数为8,每跳传送的比特数为1,信噪比SNR=20 dB。图2给出了不同干扰比例情况下的理论误码界与仿真结果,由图中可以看出,当信干比较低时,仿真结果在理论误码界之下,当信干比增大时,仿真结果与理论误码界完全重合,验证了理论推导的正确。由图中还可以看出,不同干扰比例的误码率曲线在信干比较大时重合,这是因为当信干比较大时,干扰功率较小,受干扰影响较小,此时系统性能主要由信噪比所决定。
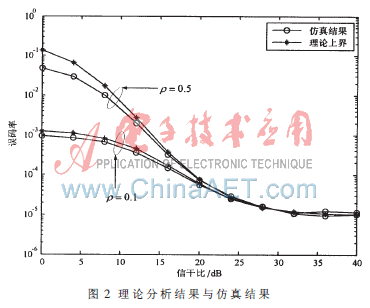
图3给出了传统线性序列合并接收机与噪声归一化接收机在不同干扰比例条件下的性能对比。仿真条件为:跳频点数N=16,每跳传送的比特数BPH=2,信噪比SNR=20 dB。由图中可以看出,噪声归一化接收机的性能明显好于性线接收机的性能。由图3还可以看出,当信干比较大时,误码率曲线趋于水平,且不同干扰比例条件下的两种接收机误码率曲线重合,这是因为当信干比增大时,干扰功率越来越小,系统性能趋近于在没有干扰条件下的差分跳频系统性能。由图3还可以看出,线性序列合并接收机在干扰比例?籽=0.5时的系统性能要好于?籽=0.1时的系统性能,而噪声归一化接收机则正好相反。这是因为,差分跳频系统可看作是一种编码调制系统,其接收端对误跳有一定的纠错能力,这种纠错能力在系统误码率小于一定数值时表现良好,但系统误码率大于一定数值时,其性能会恶化。在线性序列合并接收机中,当干扰比例减小时,干扰较集中,干扰的功率谱密度增大,干扰比例较小时的系统性能要差于干扰比例较大时的系统性能。在噪声归一化接收机中,当干扰功率较大时,由于每跳的非相干检测值采用噪声功率进行归一化处理,所以受到干扰的那跳在整个合并结果中所占的比例会随着噪声功率的增大而减小,从而减少了干扰对系统性能的影响,其性能会随着干扰比例的减小而变好。
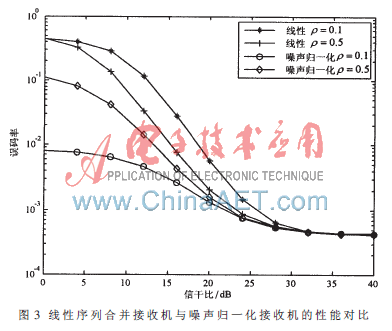
差分跳频是一种新型的跳频体制,它有机地将信号调制与跳频控制相结合,为短波通信提供了一种高速数据传输方法。提出了差分跳频噪声归一化接收机,能有效减少干扰及衰落对系统性能带来的损伤;采用复变函数相关论理,给出了噪声归一化接收机在部分频带干扰Rayleigh衰落信道下的误码界。仿真结果表明理论分析的正确性,同时也可以看出,噪声归一化接收机能显著提高差分跳频系统的抗干扰性能。
参考文献
[1] HERRICK D L, LEE P K. CHESS a new reliable high speed HF radio. MILCOM’96, 1996,3:684-690.
[2] HERRICK D L, LEE P K, LEDLOW L L. Correlated frequency hopping-an improved approach to HF spread
spectrum. Tactical communication conference,1996:319-324.
[3] 陈智,李少谦,董彬红. 差分跳频通信系统抗部分频带噪声干扰的性能分析[J]. 电子与信息学报, 2007,29(6):1324-1327.
[4] 潘武, 周世东, 姚彦. 差分跳频通信系统性能分析[J]. 电子学报, 1999,27(11):102-104.
[5] ZHU Li Ping, YAO Yan, ZHU Yi Sheng. Antijam perfor mance of FFH/BFSK with Noise-Normalization Combining in a Nakagami-m Fading Channel with Partial-Band Interference. IEEE Commun. Lett,2006(10):429-431.
[6] PROAKIS J G,Digital Communications.New York, McGraw-Hill, 2001.

