摘  要： Haenni的概率推理系统在与D-S理论相互转化的过程中进行了投影，从而不可避免地导致一些有价值信息的丢失。为此提出一种新的概率逻辑结果支持度的合成算法来避免信息的丢失。
关键词： 概率推理系统；D-S理论；合成算法

　概率推理系统的目的是根据不确定知识来判断一个未知问题，与不确定性推理中的其他理论相比，该理论既支持定量判断，也支持定性计算。它将古典逻辑和概率理论完美结合，使得在不脱离古典逻辑的领域内也能通过自然、简捷的方法得到非单调性，同时还可以利用古典逻辑的丰富计算手段进行数值计算。另一方面，概率理论是贝叶斯方法的基础，它能得到不确定性推理的更为一般的方法，概率理论的使用结果能使该理论与D-S理论进行相互转化[1-2]。概率推理系统中的计算主要是通过消除变量或命题而得到最小拟支持，这种方法的优点是对不同的公式体系[3]都适用。但在与D-S理论相互转化的过程中进行了投影，从而不可避免地导致丢失有价值的信息。为了克服这个缺陷，本文采取将一个大的概率推理系统划分为几个小的概率推理系统，从而得到不同的势，再将这些势扩充到同一空间合成的方法来避免信息的丢失。

1 D-S理论

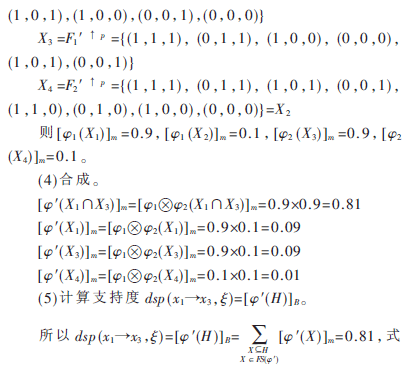
中H={(1，1，1)，(1，0，1)，(0，1，1)，(0，0，1)，(0，1，0)，(0，0，0)}。通过扩张后再合成的优点是不容易丢失有价值的信息。
参考文献
[1] KLEER J D. An assumption-based TMS[J]. Artificial Intelligence， 1986(28)：127-162.
[2] KLEER J D. Extending the ATMS[J]. Artificial Intelligence， 1986(28)：163-196.
[3] 张晨东，陈火旺，王兵山，等.概率逻辑推理的弱相关分解方法[J].计算机学报，1997，20(10)：894-898.
[4] HAENNI R， KOHLAS J， LEHMANN N. Probabilistic argumentation systems[M]. Handbook of Defeasible Reasoning and Uncertainty Management Systems，Volume 5： Algorithms for Uncertainty and Defeasible Reasoning. Kluwer Academic Publishers， 2000.
[5] 张晨东，谢兵，陈火旺，等.概率逻辑含多重原子交集分解模型的可靠性[J].计算机研究与发展，1998，35(8)：673-677.