摘  要： 提出了用递推最小二乘法辨识连续带钢热镀锌退火炉模型参数。在已建立的连续带钢热镀锌退火炉数学模型的基础上，经过分析计算确定模型参数。考虑到最小二乘法的缺陷，选用递推最小二乘法进行参数辨识，并结合实例给出辨识结果和分析，证明了该方法的可行性。
关键词： 热镀锌退火炉；数学模型；递推最小二乘法辨识

　随着连续退火工艺技术的发展，连续退火过程控制技术也得到了相应发展，尤其基于数学模型的连续带钢热镀锌退火炉控制方面的研究日趋活跃。本文就连续带钢热镀锌退火炉数学模型及其参数的辨识研究介绍如下。
1 建立系统数学模型
　根据热镀锌退火炉基本传热机理及相应的边界条件，建立退火炉带钢温度分布模型。考虑到带钢在炉内移动而引起的能量迁移，由假设及富里哀导热定律，得到描述带钢在退火炉内分布规律的二维不稳定导热方程[1]：

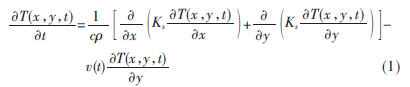
　其中，T(x，y，t)为带钢温度分布的动态响应；c为钢板的比热数；ρ为钢的密度；Ks为钢的导热系数；x、y、t为空间及时间坐标。实际计算中可以将Ks视为常数。
　式(1)是高维复杂偏微分方程，求解非常困难。为了简化计算及方便参数辨识，采用时空离散化技术对所建模型进行处理。根据时空离散化技术，经过推导得出以带温为状态变量、炉温为控制变量的带钢温度分布状态空间模型一般形式的离散结构[2]：

2 递推最小二乘参数辨识算法
　最小二乘法的基本结果有两种形式，一种是经典的一次完成算法；另一种是现代的递推算法[3]。一次完成算法多应用于理论研究方面，在具体的实际使用过程中，占用内存量大，且不适合在线辨识。为了减少计算量，节省计算机的内存，便于实时在线辨识，选用递推最小二乘法进行参数的辨识。

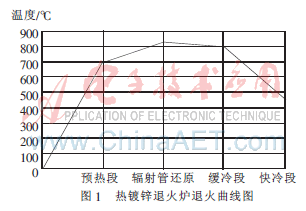
参考文献
[1] 田玉楚，侯春海.连续热镀锌退火炉的数学模型开发[J].冶金能源，1995，14(3)：38-41.
[2] 田玉楚，侯春海.带钢连续热镀锌退火过程的模型化[J].控制理论与应用，1995，12(4)：459-464.
[3] 方崇智，萧德云.过程辨识[M].北京：清华大学出版社，1988.