摘 要: 介绍了CORDIC算法的基本原理,分析了其具体计算方法。针对利用CORDIC流水线实现FFT蝶形运算耗费资源多的问题,依据CORDIC计算迭代系数的方法改进了CORDIC流水线的结构形式,使其适应FFT算法。选用 ALTERA 公司CycloneII系列的EP2C35F672C6 来实现整个FFT 处理器,并对设计进行了时序仿真和硬件仿真。通过比较,计算结果与设计基本一致。
关键词: CORDIC;FFT;Cyclone II;流水线
坐标旋转计算机CORDIC(The Coordinate Rotational Digital Computer)算法是一种用于计算一些常用的基本运算函数和算术操作的循环迭代算法。其基本思想是用一系列与运算基数相关的角度的不断偏摆来逼近所需旋转的角度,从广义上讲它是一个数值型计算逼近的方法。由于这些固定的角度与计算基数有关,运算只有移位和加/减。若用传统的乘、除等计算方法,需要占用大量的硬件资源,甚至算法是难以实现的,这样就不能满足设计者的要求。CORDIC算法正是由此产生的,它仅在硬件电路上用到了移位和加/减,大大节约了硬件资源,使得这些算法在硬件上可以得到较好地实现,从而满足设计者的要求。根据它的迭代原理,CORDIC单元可以用流水线结构表示,使向量旋转并行处理,大大加快了蝶形运算的速度[1]。但是CORDIC运算单元的多级迭代也占用了大量的芯片资源,尤其是在使用多个蝶形进行FFT处理时,使用的资源是非常巨大的,为了尽量降低资源占用,对CORDIC流水线进行了结构上的改进。
1 CORDIC算法原理
1959年,VOLDER开发了一类计算三角函数、双曲函数的算法,其中包括指数和对数运算。此算法的基本思想是用一系列固定的与运算基数相关的角度不断偏摆从而逼近所需的角度。从广义上讲它是提供一个数值计算的逼近方法。由于这些固定的角度只与计算基数有关,运算只有移位和加减。CORDIC算法虽然可以实现很多基本函数,但一开始并没有引起人们很大的注意,只是CAGGETT用它来实现二进制和十进制的转换。整个60年代没什么进展,直到1971年WALTHER提出统一的CORDIC算法,加上VLSI技术的不断发展,CORDIC算法才越来越受到人们的重视,并展示出广泛的应用前景[2]。CORDIC算法已被广泛用作现代信号处理各种算法实现中的运算单元,诸如离散傅里叶变换、矩阵的分解、矩阵特征值的求解、场分解、线性预测参数的求解等。
如图1所示,一对直角坐标轴顺时针旋转角度A(点M相对于坐标轴逆时针旋转),点M的坐标从(x0,y0)变为(x,y)[3-6]。


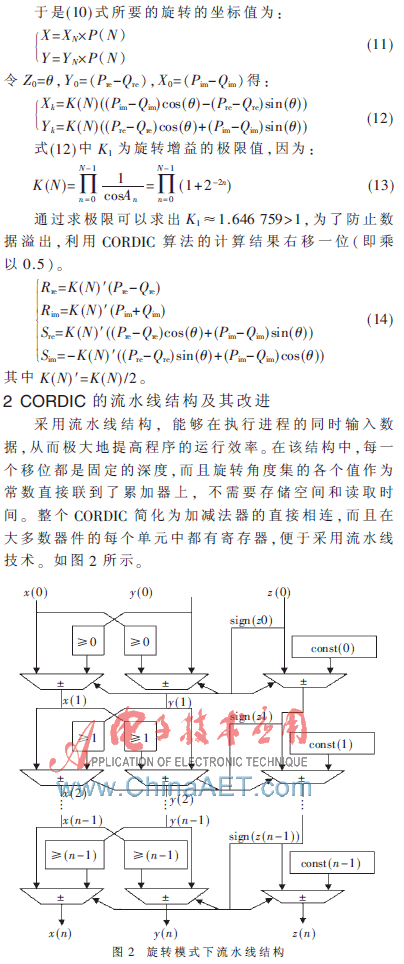
为了满足FFT在速度上的要求,CORDIC可以设计成流水线的形式。将需要旋转的角度加到Z0数据通道,通过Z1与固定角度相加减产生所取的值。需要旋转的(x0,y0)向量在各级迭代中旋转方向。Zn通过多次迭代,趋近于零,向量旋转到相应角度。如果在FFT的蝶形单元中用CORDIC代替复乘单元,只需要将数据的实部和虚部分别加到x0和y0通道,将复乘系数作为角度从Z0处输入,达到了乘以的目的。实际应用中将FFT使用的角度值存储在ROM中,由地址发生器控制,在计算时将相应的旋转角度读入CORDIC中即可。使用CORDIC算法可以方便快捷地计算FFT蝶形,但是由于迭代次数多,导致耗费资源也比较多。
将CORDIC流水线形式进行改进,如图3所示,需要旋转的向量的实部和虚部分别加到X0和Y0数据通道上,系数输入到D触发器中与向量保持同步,用来控制向量在各级迭代中旋转的方向。向量经多次迭代旋转到相应角度[7-8]。

3 CORDIC的旋转系数
按照改进后CORDIC的结构,需要事先求出CORDIC的旋转系数。根据CORDIC 算法的迭代原理以及此结构的具体情况,使用 MATLAB 语言编写程序求出各级旋转系数,存在ROM中。时序仿真结果如图4所示。

图4是利用改进的CORDIC算法计算的结果。从仿真图可以看出:当输入不同的迭代系数C时,就可以计算出不同的结果。
4 FFT处理器的仿真和测试
在完成了FFT的整体设计和具体模块设计之后,选用ALTERA公司CycloneII系列的EP2C35F672C6来实现整个FFT处理器,并对设计进行了时序仿真和硬件仿真[9-10]。
(1)直流信号的测试
使用MATLAB产生一个直流信号:i=1:256,x(i)=50。输出计算结果和MATLAB的计算结果比较如图5所示,MATLAB计算的直流信号FFT结果虚部全为0,实部只有一个值即:X(0)=14 000;FFT处理器的计算结果也一样:X(0)=6 000,如图6所示。因为运用CORDIC算法一方面使运算每一级的结果扩大了1.65倍,另一方面为了减少误差和防止溢出,在FFT处理器的各级都进行了1/2的截尾处理。但是这样的处理不会影响频谱的显示。

(2)三角波信号的测试
仍然使用MATLAB:i=1:128,x(i)=i;(28+i)=128,产生一个三角波信号。MATLAB的计算结果见图7和图8,FFT 处理器中输出计算结果见图9和图10。由于FFT 处理器对各级进行了放大和截尾处理,所以为了便于比较,将FFT处理的结果进行了还原(即除以1.65^3/16),通过图对实部和虚部进行比较,可以证明计算结果基本一致。

采用CORDIC算法以较少的资源实现了快速乘法器,通过增加CORDIC运算单元的处理位数,减少了算法的误差。设计使用16位宽,CORDIC单元的误差不大于2-14,有效位数为13位。FFT有限字长效应长生量化误差,主要来自输入量化误差、系统量化误差和运算量化误差。从仿真实验可以看出,达到了预期目的。
参考文献
[1] 胡国荣,孙允恭.CORDIC算法及其应用[J].信号处理,1991(12):229-242.
[2] VOLDER J E.The CORDIC trigonometric computing technique[J].IRE TlectronComputers,1959(9):330-334.
[3] 于效宇,宋立新,刘艳.CORDIC流水线结构在FFT设计中的改进[J].哈尔滨理工大学学报,2005,10(1):55-57.
[4] 韩芳,初建朋,赖宗声.一种CORDIC算法的精度分析及其在FFT中的应用[J].微电子学与计算机,2004,7(7):14-16.
[5] 于效宇.基于FPGA的FFT处理器的实现[D].哈尔滨:哈尔滨理工大学,2005.
[6] 李成诗,初建朋,李新兵.基于CORDIC的一种高速实时定点FFT的FPGA实现[J].微电子学与计算机,2004,21(4):88-91.
[7] 杨宏,李国辉,刘立新.基于FPGA的CORDIC算法的实现[J].西安邮电学院学报,2008,3(1):75-77.
[8] 杨宇,毛志刚,来逢昌.一种改进的流水线CORDIC算法结构[J].微处理机,2006(4):10-13.
[9] 张俊涛,王红仓.基于FPGA的CORDIC算法通用IP核设计[J].微计算机信息,2008,24(7-3):238-240.
[10] 刘桂华,傅佑麟,严平.FFT实时谱分析系统的FPGA设计和实现[J].集成电路应用,2005(4):65-67.

