摘 要: 研究了在加性高斯白噪声(AWGN)信道中采用最小频移键控(MSK)调制的Raptor码的译码算法设计问题。基于Raptor码和MSK调制的特点,提出了一种改进的Raptor码置信传播译码算法。仿真结果证明该译码算法具有更好的译码性能。
关键词: Raptor码;因子图;AWGN信道;置信传播译码
继Turbo码和LDPC码之后,喷泉码成为了近年来纠错码领域新的研究热点[1]。喷泉码由于其无比率特性非常适用于时变信道。目前主要的两类喷泉码是LT码[2]和Raptor码[3]。Raptor码是LT码的一种扩展,它由预编码和LT码两部分组成。Shokrollahi等人设计的系统Raptor码已被第三代蜂窝网络多媒体广播/多点传送服务标准所采用。Raptor码最初是为在删除信道中应用而提出的,现已证明在加性高斯白噪声AWGN(Additive White Gaussian Noise)信道和衰落信道中Raptor码同样拥有接近信道容量的性能[4-6]。
参考文献[4]和参考文献[5]中对Raptor码在AWGN信道中采用二进制相移键控BPSK(Binary Phase Shift Keying)调制的设计问题进行了深入研究,给出了Raptor码在AWGN信道中的置信传播BP(Belief Propagation)软判决译码算法,其原理为先进行LT码译码再进行预编码译码。最小频移键控MSK(Minimum Shift Keying)由于其属于恒包络调制和良好的频谱特性已被广泛应用。本文研究了采用MSK调制的无线系统中Raptor码译码算法的设计问题,给出了一种类似于Turbo码译码的算法。仿真性能表明所提出的Raptor码译码算法优于参考文献[4]中的译码算法。
1 Raptor码及其BP译码算法
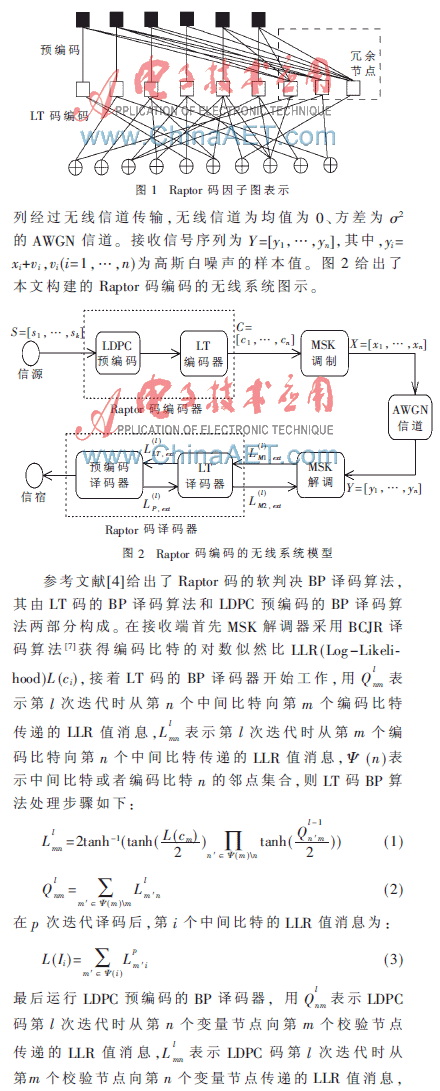
Raptor码是一种级联码,其编码过程由预编码过程和LT码编码过程组成。预编码通常选用高码率的线性分组码,本文中采用了LDPC码作为预编码。预编码过程将输入的信息比特通过传统的编码转换为中间比特,中间比特再进行编码比特度分布函数为Ω(x)的LT码编码,从而得到Raptor码的编码比特。
相比于LT码,Raptor码中由于预编码有一定的纠错能力,放宽了对编码比特度分布函数?赘(x)的设计要求,从而整体降低了编译码的复杂度。图1给出了Raptor码的因子图表示。


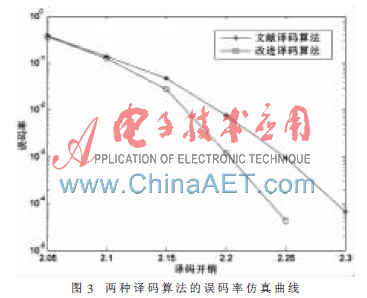
Raptor码译码器分别采用了参考文献[4]中BP译码算法和本文提出的改进BP译码算法。参考文献[4]BP译码算法中LT码译码器和LDPC码译码器各执行80次迭代译码。改进BP译码算法也进行了80次迭代译码。图3给出了在不同译码开销?酌下两种译码算法的误码率,由图可知,本文所提算法能获得更好的译码性能。
本文研究了在AWGN信道中传输Raptor码的译码器设计问题,针对MSK调制和Raptor码的特点提出了一种改进的Raptor码译码算法。仿真结果证明了算法的优越性,为Raptor码在无线通信中的应用提供了新的依据。
参考文献
[1] 穆建君, 焦晓, 曹训志.数字喷泉码及其应用的研究与展望[J].电子学报, 2009, 37(7): 1571-1577.
[2] LUBY M.LT codes[C].Proc 43ed Ann IEEE Symp on Foundations of Computer Science, Vancouver, BC, Canada,2002: 271-282.
[3] SHOKROLLAHI A.Raptor codes[J].IEEE Trans Inform Theory, 2006, 52(6): 2551-2567.
[4] ETESAMI O, SHOKROLLAHI A.Raptor codes on binary memoryless symmetric channels[J].IEEE Trans Inform Theory, 2006. 52(5): 2033-2051.
[5] CHENG Z, CASTURA J, MAO Y.On the design of raptor codes for binary-input Gaussian cahnnels[J].IEEE Trans Commun, 2009,57(11): 3269-3277.
[6] 袁磊, 安建平, 李祥明.喷泉码在无线中继网络中的应用[J].信息通信技术, 2009, 12(6): 61-65.
[7] BAHL L, COCKE J, JELINEK F, et al.Optimal decoding of linear codes for minimizing symbol error rate[J].IEEE Trans Inform Theory,1974, 20(2): 284-287.
[8] RIMOLDI B.A decomposition approach to CPM[J].IEEE Trans Inform Theory,1988, 34(2): 260-270.
[9] HU X, ELEFTHERIOU E, ARNOLD D.Regular and irregular progressive edge-growth tanner graphs[J].IEEE Trans Inform Theory,2005, 51(1): 386-398.

