摘 要: 张量主成分分析法(TPCA)用于人脸特征提取,克服了传统的基于统计特征的特征提取方法会破坏图像原始结构的问题;而源图像经过非下采样剪切波变换后得到了k个大小相同但尺度不同的带通图像,具有良好的时频分析特征。为了更好地提取人脸识别特征,提出了非下采样剪切波融合TPCA的人脸特征提取算法,该算法先对源图像进行非下采样剪切波变换得到4个子代图像,再对子代图像进行TPCA特征提取得到特征集,实现人脸的高效识别。实验结果表明,该算法明显优于原有的单一算法。
关键词: 非下采样剪切波变换;张量主成分分析;特征提取;人脸识别
人脸识别技术有着十分广阔的研究前景,在许多领域得到了应用。人脸识别的特征提取是决定人脸识别准确率的关键性因素之一,其目标是用最少的特征来表征人脸,同时又可以最大程度地区分人脸,研究表明:不同的人脸特征提取方法对人脸识别的性能影响很大[1]。提取人脸特征的方法分为基于几何特征和基于统计特征两种,近年来所提出的方法主要是基于统计特征[2]。主成分分析法(PCA)是一种经典的基于统计特征的人脸特征提取方法[3],其主要思想是:把人脸图像展开成高维的行或列向量,然后计算这些向量的协方差矩阵的特征向量所组成的投影矩阵,最后通过投影矩阵把原始训练样本的高维向量投影到低维向量。但是这种方法有以下问题:(1)图像展开成向量的形式,破坏了图像的原始空间结构;(2)图像展成高维的向量容易造成维数灾难;(3)求解样本的协方差矩阵需要大量的存储空间和计算量。
为了解决PCA算法提取人脸特征的不足,提出了张量主成分分析法(TPCA)进行人脸特征的提取[4-8]。TPCA将图像看成二阶张量空间中的点,投影后的特征既能有效地保持张量图像像点之间的空间关系,又能良好地保持蕴含在张量图像之间的类内关系,提高了人脸特征提取的准确性。
非下采样剪切波变换将图像分解成4个子代图像,每个子代图像的面积与当前图像的面积相等,其中一个子代图像对应图像的低通部分,保留了当前图像的主要信息;而其他3个子带图像对应当前图像的高通部分,保留了当前图像的细节信息。
非下采样剪切波融合TCPA的人脸特征提取算法的主要思想是:首先对图像做非下采样剪切波变换,然后再用TPCA进行特征提取,并分别在3个人脸数据库ORL、FLD、FERET及自建库进行实验,得到了更高的识别率。
1 非下采样剪切波变换
非下采样剪切波变换过程主要分为以下两部分[9]:
(1)非下采样金字塔(NSP)分解
首先采用二通道的非下采样滤波器组使得非下采样剪切波具备了多尺度的性质,原来的图像经过一级NSP分解可产生一个低通的子代图像,之后的每一级NSP分解都在低通分量上进行迭代,得到图像中的奇异点。所以,二维的图像经过k级NSP分解后,可得到1个低通图像和k个大小相同但尺度不同的子带通图像。
(2)方向局部化
方向局部化是通过剪切波器(SF)实现的。通过伪极化坐标映射到笛卡尔坐标,运用Meyer小波构造窗口函数,得到剪切波滤波器,将分解后的带通子代图像与Meyer窗口函数进行二维卷积运算,得到方向子代图像。

自建库中图像及其一层非下采样剪切波变换图像如图1所示。非下采样剪切波变换的过程不存在下采样操作,所以避免了下采样变换的不足,使其具有平移不变性,同时具备了非常好的局部特性、较高的方向敏感性和尺度化的抛物线特性等。
2 张量主成分分析法(TPCA)
假设一个图像矩阵为X∈RW×H,利用二阶TPCA对X来进行特征提取,首先要得到两个投影矩阵U∈RW×l1和V∈RH×l2,把X投影到低维的矩阵子空间:
Y=UTXV∈Rl1×l2(1)
两个最优的投影矩阵U、V可以通过计算Y和X的最小重构方差得到[10]:

参考文献[11]给出了求解U、V的步骤,前提是样本的均值矩阵全为零矩阵,而且需要计算样本间的相关协方差矩阵,本文改进参考文献[11]的方法,如表1所示。

3 算法实现过程
首先对人脸图像进行非下采样剪切波变换得到4个子代图像,然后对子代图像进行特征提取,最后用最邻近法进行人脸的分类。图像经过非下采样剪切波变换产生的4个子代图像对表征图像特征的贡献率不同,赋予它们不同的权值,权值满足:
w1+w2+w3+w4=1(3)
给出训练样本图像Xi,它是从每类图像中抽取的一些图像,其余的图像就组成了测试样本图像Yj。对每个Xi进行非下采样剪切波变换得到4个子代图像,再用TPCA进行特征提取得到训练样本特征集合Xi1,Xi2,Xi3,Xi4。对Yj进行同样处理,得到测试样本特征集合Yj1,Yj2,Yj3,Yj4。
根据与Yj距离最小的Xi来判断Yj所属的类别,利用式(4)计算测试样本特征集合和训练样本特征集合之间的距离:
dist(Yj,Xi)=w1dis(Yj1,Xi1)+w2dis(Yj2,Xi2)+w3dis(Yj3, Xi3)+w4dis(Yj4,Xi4)(4)
其中,dis(·)算子的计算方法为:
dis(X,Y)=sqrt(trace((X-Y)*(X-Y))T)(5)
4 实验分析
采用4个人脸图像数据库进行实验,分别是:ORL、FLD、FERET和自建库。ORL人脸数据库包括40类共400张人脸图像。FLD人脸数据库是彩色的,在进行人脸识别之前先把图像处理成灰度图像,包括10类共20张人脸图像。FERET人脸数据库包括200类共1 400张人脸图像。现有的数据库不足以检验算法的准确性,所以根据需要建立了一个自建库,选取了10类不同的人脸,分别在不同光照、不同角度甚至不同配饰下拍摄图片20幅。
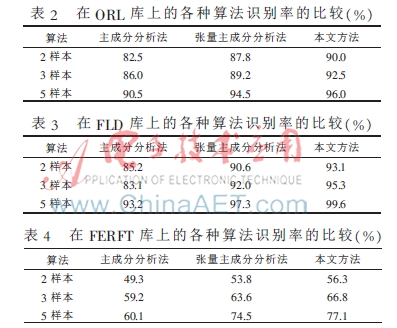
表2~4给出了分别选取2个样本、3个样本和5个样本作为训练集,采用PCA、TPCA和本文方法进行人脸识别时的平均最高识别率。可以看出,对于所有的识别算法,随着训练样本数量的增加识别率有所提高,而基于张量的算法在识别性能上优于基于向量的算法,本文算法明显优于以上两者。

在自建库上的各种算法识别率的比较如表5所示。自建库中每类每个图像的表情和姿势变换很大,眼睛和嘴部的变换很明显,其他几类数据库没有这样的情况,所以该实验的识别率不是很高,但也可以作为参考。
非下采样剪切波变换融合TPCA的人脸识别算法,采用TPCA对非下采样剪切波变换后的子图像进行特征提取,得到了具有良好分辨能力的图像特征,识别算法优于单一的张量算法或者非下采样算法。尽管张量算法优于普通的向量算法,但是张量算法只是考虑图像中同一行或同一列的像素间的关系,而没有考虑图像的全部空间关系,而且目前该方法只适用于图像数据,但是很容易将其扩散到高阶张量,从而处理一些视频数据,这是进行下一步研究的重点问题。
参考文献
[1] Tao Liang, Zhuang Zhenquan. An effective approach for frontal face verification[J]. Journal of image and Graphics, 2003, 8(A):1-3.
[2] Liu Qingshan, Lu Hanqing, Ma Songde. A survey: subspace analysis for face recognition[J]. Automatica Sinica,2003, 129(16):900-911.
[3] BELHUMEUR P N, HESPANHA J P, KRIENGMAN D J.Eigen faces vs. Fisher faces[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997:19(7):711-720.
[4] He Xiaofei, Cai Deng, NIYOGI P. Tensor subspace analysis[EB/OL].[2008-7-1]http://books.nips.cc/papers/files/nips18/NIPS2005_2049.pdf.
[5] Yan Shuicheng, Xu Dong, LIN S, et al. Element rearrangement for tensor-based subspace learning[C]. IEEE Conference on Computer Vision and Patten, 2007: 1-8.
[6] Xu Dong, Yan Shuicheng, Zhang Lei, et al. Concurrent subspaces analysis[C]. San Diego: IEEE Conference on Computer Vision and Patten, 2005:203-208.
[7] 杨颖娴.一种基于模糊支持向量机的人脸识别新算法[J].微型机与应用,2012,31(15):43-44.
[8] 张九龙,夏春莉,张志禹,等.基于多尺度分析的人脸识别比较研究[J].微型机与应用,2011,30(7):46-49.
[9] Gao Yinhan, Chen Guangqiu, Liu Yanyan. Adaptive image fusion based on image quality assessment parameter in NSST system[J]. Journal of Jilin University, 2014:3-4.
[10] PUYATI W, WALAIRACHT S, WALAIRACHT A. PCA in wavelet domain for face recognition[C]. The 8th International Conference on Advanced Communicaltion Technology, ICACT 2006,2006:450-456.
[11] Xu Dong, Yan Shuicheng, Zhang Lei. Coupled subspaces analysis[EB/OL]. [2008-07-10]ftp://ftp.research.microsoft.com/pub/tr/TR-2004-106.pdf

