文献标识码: A
文章编号: 0258-7998(2015)04-0108-04
0 引言
双向中继技术[1-4]的基本思想是:通过中继节点将接收到的两用户混合信号先进行线性处理,再经过广播发送回两用户,每个用户对中继发来的信息进行自干扰消除后即可获得对方用户的信息。传统的协作模式需要四个传输时隙来完成该过程,双向中继技术仅需要两个传输时隙完成信息交互过程,这大大减少了多用户传输的资源开销,提高了系统传输效率及吞吐量。在双向中继技术中,中继节点对于多用户混合接收信号的检测能力是决定该技术性能优势的关键所在[5]。因此,如何实现中继节点高效且低复杂度的多用户接收机是目前亟待解决的问题。
本文针对双向中继系统建立了中继节点多用户接收机因子图模型,通过利用高斯参数化对混合高斯分布的近似,提出了一种联合信道估计、多用户检测与译码的迭代消息传递算法,在合理的复杂度下有效提高了中继接收机对于多用户混合信号的检测性能。
1 双向中继系统模型
半双工约束下的单天线双向中继协作通信系统在没有直接通信链路的情况下,两个用户U1与U2通过中继节点R进行信息交互。双向中继系统的基本思想是通过利用无线信道的广播特性,减少用户间信息交互所需的传输时隙,从而有效地提高系统的传输效率与吞吐量。双向中继传输方案通常仅需要两个传输时隙:多址时隙与广播时隙。在多址时隙中,用户U1与U2同时向中继节点R发送信息,中继节点R需要对两个用户的叠加基带信号进行检测。在广播时隙,中继节点R将两用户信息的模2和广播给各个用户。用户利用自身信息对接收到的广播信号进行干扰消除,即可得到另一用户的信息。双向中继系统的基本结构如图1所示。
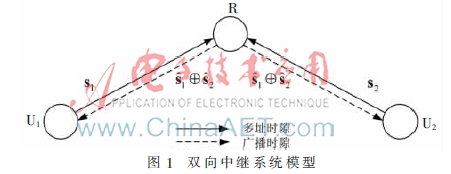
在多址时隙,两个用户产生均匀且独立同分布的信息比特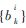 ,其中i∈{1,2}分别表示用户1与用户2的信息。经过LDPC编码及线性调制后生成发送符号序列
,其中i∈{1,2}分别表示用户1与用户2的信息。经过LDPC编码及线性调制后生成发送符号序列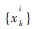 。为了得到信道的初始估计,在发送符号序列中周期地插入导频符号。此时,中继节点R接收到的混合信号可表示为:
。为了得到信道的初始估计,在发送符号序列中周期地插入导频符号。此时,中继节点R接收到的混合信号可表示为:



式中: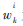 为独立同分布的零均值复高斯随机变量,方差为
为独立同分布的零均值复高斯随机变量,方差为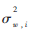 。
。
2 中继节点迭代接收机设计
本文将因子图方法应用于中继节点的多用户接收机设计中,建立两用户双向中继的因子图模型,并基于因子图上的消息传递,提出了一种适用于中继节点接收机的联合迭代信道估计、多用户检测与译码算法。在多址传输时隙,中继节点接收到两个用户同时发送的混合信号,此时联合后验概率分布可因式分解为:
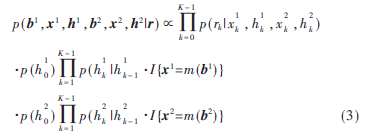
式中I{xi=m(bi),i∈{1,2}分别表示用户1与用户2的编码调制映射指示函数,若xi为对应于bi的合法复调制编码序列,则指示函数为1,否则为0。式(3)的推导中,分别利用了信息比特的均匀独立同分布特性、AWGN信道的无记忆特性以及衰落信道系数的AR模型假设。因式分解式(3)对应的因子图模型如图2所示。其中函数节点对应的函数定义为:
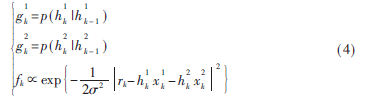
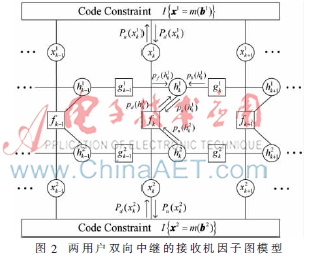
为了在中继节点得到有效且低复杂度的信号检测算法,在双向中继接收机的因子图模型上应用了SP算法。图2给出了第k时刻用户1各边上的消息表示,用户2的消息与用户1对称。其中,P(·)表示消息为离散变量的概率质量函数,p(·)表示消息为连续变量的概率密度函数。对于用户1的变量节点![(%JH_]V8U{)38[7JWEJ(U[4.png (%JH_]V8U{)38[7JWEJ(U[4.png](http://files.chinaaet.com/images/2015/07/27/6357361729792978914388679.png) ,消息
,消息![)TS4Y(VU4]7P1[N`2NCT0MR.png )TS4Y(VU4]7P1[N`2NCT0MR.png](http://files.chinaaet.com/images/2015/07/27/6357361730778278919709232.png) 表示发送至译码器的编码符号后验概率,而
表示发送至译码器的编码符号后验概率,而![T]17)GFYMYN{3K3(9B9`(RD.png T]17)GFYMYN{3K3(9B9`(RD.png](http://files.chinaaet.com/images/2015/07/27/6357361732176478914858608.png) 表示译码器更新后的编码符号后验概率。
表示译码器更新后的编码符号后验概率。
因子图的消息迭代更新过程如下:首先用户1进行信道估计,解映射与LDPC译码,随后用户2进行信道估计、解映射与LDPC译码,信道估计与译码输出的软信息在对应于因子图上、下两部分的检测器间迭代地传递,直到算法达到收敛。由于因子图的对称性,这里仅对因子图上半部分的消息更新进行推导。
首先,采用高斯近似方法。假设用户2的消息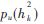 具有高斯分布形式:
具有高斯分布形式:

根据SP算法法则,消息![TARYO{}@[0]H}5L`SWM}3XL.png TARYO{}@[0]H}5L`SWM}3XL.png](http://files.chinaaet.com/images/2015/07/27/6357361742893678912379803.png) 可计算如下;
可计算如下;
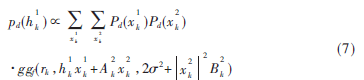
此时消息![TARYO{}@[0]H}5L`SWM}3XL.png TARYO{}@[0]H}5L`SWM}3XL.png](http://files.chinaaet.com/images/2015/07/27/6357361744001478915824823.png) 为混合高斯分布形式,进一步利用最小发散度(KL距离)的高斯分布来近似混合高斯分布消息
为混合高斯分布形式,进一步利用最小发散度(KL距离)的高斯分布来近似混合高斯分布消息![TARYO{}@[0]H}5L`SWM}3XL.png TARYO{}@[0]H}5L`SWM}3XL.png](http://files.chinaaet.com/images/2015/07/27/6357361744926178915434057.png) ,表示为:
,表示为:
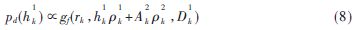
其中:
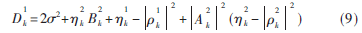
式中,![E_B4QIFTZ]]_DY_BLV$VOX2.png E_B4QIFTZ]]_DY_BLV$VOX2.png](http://files.chinaaet.com/images/2015/07/27/6357361772567578913278535.png) 分别为用户1和用户2第k时刻发送符号的后验均值与均方值。在式(8)的高斯近似下,结合时变信道的AR模型,用户1的信道估计子图转化为线性高斯系统。因此,采用前向-后向的递归消息传递,如图3所示,其中前向与后向消息均为高斯分布形式。
分别为用户1和用户2第k时刻发送符号的后验均值与均方值。在式(8)的高斯近似下,结合时变信道的AR模型,用户1的信道估计子图转化为线性高斯系统。因此,采用前向-后向的递归消息传递,如图3所示,其中前向与后向消息均为高斯分布形式。
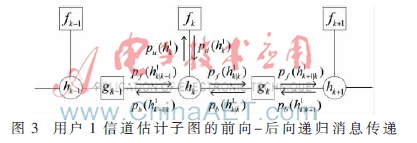
经过前向与后向高斯消息参数的递归计算,可得:

其中:
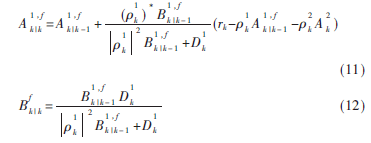
第k+1时刻的前向消息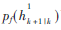 可计算为:
可计算为:
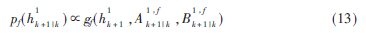

其中k=0,K,K-1,前向递归的初始化条件设定为![F~OWY41D[A$9BMU(K7EM]%C.png](http://files.chinaaet.com/images/2015/07/27/6357361775860878916399974.png)
![OWX]T1_UN9A9QNUZSE__SNG.jpg](http://files.chinaaet.com/images/2015/07/27/6357361775876178913357698.jpg) 。
。
类似于前向消息的递归推导,后向消息的参数递归计算如下:
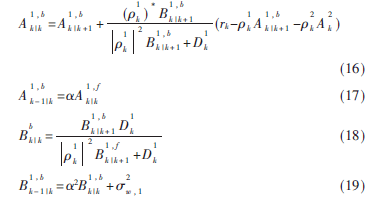
其中k=K-1,K,0,初始化条件为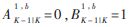 。
。
通过前向与后向消息,可以计算用户1信道估计子图的输出消息参数为:
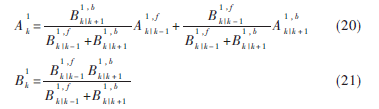
最终,利用用户1与用户2的信道估计输出消息,可得消息的计算式为:
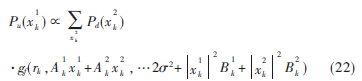
由于中继系统采用了LDPC编码调制,SP算法在因子图编码约束节点的应用对应标准的BP迭代译码算法。用户1译码器利用BP译码算法计算编码比特的后验对数似然比信息![)%@CT~(CE8BI]}C@73I4D94.png )%@CT~(CE8BI]}C@73I4D94.png](http://files.chinaaet.com/images/2015/07/27/6357361788493278916309448.png) ,经过重新映射生成编码符号的后验概率消息
,经过重新映射生成编码符号的后验概率消息 。至此,通过以上的信道估计、检测与译码过程,完成了对因子图上半部分(用户1)的消息传递与更新。由于因子图的对称性,在对应于用户2的下半部分重复以上的消息传递与更新,即可在中继接收机中完成一次完整的迭代过程。经过多次迭代之后,译码器分别输出用户1与用户2的信息比特判决。
。至此,通过以上的信道估计、检测与译码过程,完成了对因子图上半部分(用户1)的消息传递与更新。由于因子图的对称性,在对应于用户2的下半部分重复以上的消息传递与更新,即可在中继接收机中完成一次完整的迭代过程。经过多次迭代之后,译码器分别输出用户1与用户2的信息比特判决。
3 系统性能分析
本节给出了双向中继系统中基于因子图的迭代信道估计、多用户检测与译码算法的误比特率性能。两用户理想信道对应于中继接收机完全已知两用户上行衰落信道系数时的迭代消息传递算法性能;单用户非理想信道对应于当仅有单个用户与中继进行通信时的迭代消息传递算法性能[6]。仿真采用1/2码率、码长为4 000的规则LDPC码,Gray映射的QPSK调制方式。假设两用户采用相同的发射功率和编码调制方案,并且上行信道具有相同的衰落特性,归一化多普勒频移为fDT=0.005。设导频符号间隔为N=21,因子图中总的迭代次数为3次,每个仿真点的仿真次数为10 000次。
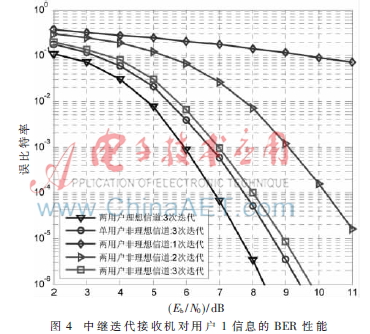
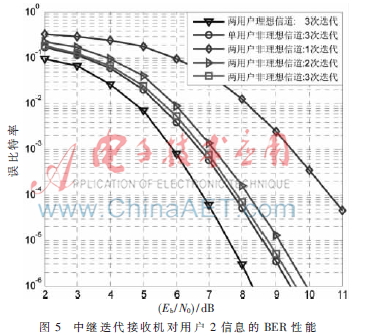
由图4与图5可见,经过3次迭代,中继接收机对用户1与用户2的译码性能均已收敛于单用户非理想信道情况,当BER=10-5时,仅存在约0.35 dB和0.15 dB的Eb/N0损失,由此证明了所提出的迭代消息传递算法具有良好的多用户检测能力。在计算复杂度方面,由于算法中将包含多个符号变量的混合高斯分布消息近似为单高斯分布函数,在应用SP算法的过程中避免了对混合高斯分布的高复杂度积分运算,因此显著降低了迭代算法的计算复杂度。
4 结论
因子图与和积算法能够直观表示函数的因式分解并高效地计算复杂函数的边缘函数。本文利用了这种新颖的迭代接收机设计方法,在时变瑞利衰落信道下,利用因子图工具建立了两用户双向中继系统的中继节点接收机因子图模型,并且提出了一种联合信道估计、多用户检测与译码的迭代消息传递算法。通过采用高斯分布对混合高斯消息进行近似,使中继接收机在可接受的实现复杂度下能够获得良好的多用户混合信号检测性能。
参考文献
[1] WU Y,CHOU P A,KUNG S Y.Information exchange in wireless networks with network coding and physical-layer broadcast[R].Microsoft Research Redmond,SR-TR-2004-78,2004.
[2] FRAGOULI C,BOUDEC J Y,WIDNER J.Network coding:an instant primer[J].ACM SIGCOMM Computer Communi-cation Review,2006,36(1):63-68.
[3] ZHANG S,LIEW S,LAM P.Hot topic:physical-layer net-work coding[C].The 12th Annual International Conference on Mobile Computing and Networking,2006:358-365.
[4] RATNAKAR N,KRAMER G.The multicast capacity of deterministic relay networks with no interference[J].IEEE Transaction on Information Theory,2006,52(6):2425-2432.
[5] SIMON M K,ALOUINI M S.Digital communication over fading channels,2nd ed[M].New York:John Wiley and Sons,2004.
[6] KIM S J,MITRAN P,TAROKH V.Performance bounds for bidirectional coded cooperation protocols[J].IEEE Transac-tion on Information Theory,2008,54(11):5235-5241.

