文献标识码: A
DOI:10.16157/j.issn.0258-7998.2015.09.020
中文引用格式: 张旭,王春明,刘洪,等. 基于双向链表排序的系统误差稳健配准方法[J].电子技术应用,2015,41(9):74-77,81.
英文引用格式: Zhang Xu,Wang Chunming,Liu Hong,et al. A robust method of system error registration based on the sorting of bidirectional linked list[J].Application of Electronic Technique,2015,41(9):74-77,81.
0 引言
电子信息装备测量数据通常会含有一些粗差,尤其在复杂电磁环境下,还会因干扰、目标丢失等原因含有较多、连续、甚至是带较大系统偏差的粗差。此时,基于白噪声假设和最小二乘原理的传统方法在数据处理中可能表现很差,需要采用一些稳健方法对多源测量数据进行融合处理。
数据融合收集、处理多个测量设备数据,通过设备之间的性能互补和相互协调,克服单个设备的不确定性和局限性,具有降低虚警率、增大数据覆盖面、提高目标探测识别与跟踪能力、增强系统故障容错与鲁棒性等优点。但由于不同来源测量数据的获取时刻和参考坐标系往往不同,要进行有效融合,就必须要将各测量信息转换到相同的时空坐标系下,即进行时空配准。时空配准是数据融合的基础,也是关键环节之一。其中系统误差配准的任务就是克服多测量设备不同的固有系统误差,对目标的空间探测信息进行校准,实现多设备探测同一目标的空间迭合。
对于系统误差配准问题,很多文献进行了讨论,提出了许多各有特点的不同方法。其中,扩维配准算法[1]和Kalman滤波法(KF)[2,3]中,系统误差估计与目标状态估计相互耦合,当目标机动时,估计结果可信度降低。同时,它们与最小二乘法(LS)[4]、期望最大法(EM)(或极大似然法)[2,5]以及实时质量控制法(RTQC)[6]受误差特性影响较大,假设合理与否直接影响算法的性能。同时,以上文献均利用仿真数据对算法进行测试,未给出实测数据下的测试结果。
本文以稳健统计理论为基础,重点讨论高样本崩溃点的系统误差稳健配准方法,并与多源测量数据融合检择结合研究,用融合结果验证配准算法,同时将提出的方法与最小二乘法相比较,用典型实测数据对算法进行测试分析。
1 问题描述
假设经过数据关联、时间配准和坐标转换(通常转至同一直角坐标)之后,在X轴方向上得到设备A、B对同一目标相同采样频率的测量序列Xi、X,那么系统误差配准就是要尽可能分离出(Xi-X)中固定不变或按确定规律变化的分量,即设备A测量数据在X方向上相对于设备B测量数据的系统误差。由于系统误差的不变性或缓变性,可以认为局部(Xi-X)为平稳序列,系统误差配准只需估计出其数学期望即可。
数学期望最基本的估计方法是均值法,此外,系统误差配准中还可以采用引言中列举的几种估计方法。以下主要介绍最小二乘法、本文提出的基于双向链表排序的中值估计算法以及与融合检择相结合的配准方法。
2 系统误差估计的最小二乘方法
2.1 最小二乘法
最小二乘法线性拟合考虑一个用n个数据点拟合成直线的问题,直线模型为:
y(x)=ax+b(1)
这个问题称为最小二乘线性回归,给定n组观测数据(xi,yi),为确定回归系数a、b,只需使下式达到最小:

最终得到拟合直线方程和相应估计值。
2.2 改进的最小二乘法
最小二乘法是在测量误差无偏、正态分布和相互独立的假定条件下[7]给出的,不具备稳健性。为减小非假定条件下误差的影响,本文给出一种改进的最小二乘法,即将最小二乘法与均值估计结合起来,先对(xi,yi)进行均值估计,得到其局部均值估计序列进行最小二乘线性拟合,进而得到相应的拟合方程和预测值。
3 基于双向链表排序的实时中值估计算法
3.1 中值估计的稳健性
稳健统计研究具有稳健性的统计方法,中值估计是一种基本的稳健估计方法。对采样序列yi,其中值为:

其中,y(j)表示对数据{y1,y2,…,ym}按从大到小排序后的第j个数值。
中值估计是按极小化极大准则的一种最优估计,其影响函数有界,样本崩溃点接近50%[8,9],因此中值估计有良好的稳健性。尤其当过失值不对称,而可能产生较大的系统偏差时,使用样本中位数,能够避免造成大的偏差。中值估计通常可用于某些辅助估计之中,以提供工程应用中十分重要的高样本崩溃点这一性质,也可直接用于缓变序列的实时估计,因此,针对配准中设备间系统误差的估计问题,设计了实时中值估计算法。
3.2 算法设计
由于中值估计需要对采样序列进行排序,从节省内存、减少运算的角度出发,选定带插入顺序和数值大小顺序索引的双向链表作为算法实现的基本数据结构。插入顺序索引确保节点先入先出,数值大小顺序索引用来定位中值,链表向前和向后的双向指针赋予算法更大的灵活性。排序算法选用插入排序,因为它更适合向有序表中添加元素。
以下为Delphi下本文双向链表的定义示例:
type
PBHNode=^TBHNode; //指针
TBHNode=record
next: PBHNode; //向后的指针
prior:PBHNode; //向前的指针
nu:integer; //节点插入顺序
x:double; //x值
shx:integer; // x值在链表中的大小顺序
end;
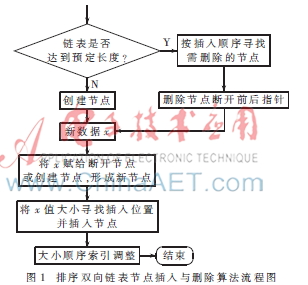
图1为双向链表排序的主要算法流程。
4 基于融合检择与系统误差实时中值估计的配准方法
4.1 融合检择
多源测量数据融合检择可通过交叉检验来识别自检择难以发现的粗差,比如偏差型斑点(连续的含较大系统偏差的异常值),利用冗余信息,提高粗差检择的可靠性。融合检择中,除聚类算法中的最近邻法之外,还可应用作者提出的中值互检择方法。
首先,通过测元自检择,完成算法初始化;采用同一预测值对多源测量数据进行检择。当只有一个设备测量值通过检择时,该测量值进入滤波器。当多个设备数据通过检择时,最近邻法选择与预测值最近的测量值进入滤波器,中值法求取多设备测量值的中位数(当通过检择的设备较少时,预测值也参与中位数计算)进入滤波器。当全部设备均未通过检择时,可选择预测值作为融合检择结果进入滤波器;当长度超出算法容错能力的数据帧出现所有设备测量数据均无法通过检择时,即可认为多设备测量系统所有设备均发生了目标丢失、干扰、设备故障或操作失误,此时应重新进行初始化判断。
4.2 基于融合检择与系统误差实时中值估计的配准方法
4.2.1 配准原则
系统误差配准应首先选择基准设备,综合考虑以下原则确定配准方案:(1)选择跟踪性能较好、修正后系统误差较小的设备作为基准设备;(2)选择先抓住目标的设备作为基准设备;(3)电子装备试验数据处理中,在测量机制不同的标准设备数据融合时,可选择与被试设备测量机制相同的标准设备作为基准设备。
4.2.2 配准方法
将当前时刻之前一定样本容量的设备间一次差的中值作为当前时刻设备间系统误差的估计值,算法实现应用上文提出的基于双向链表排序的实时中值估计算法。同时,考虑到数据融合中配准、剔点等过程之间的相互影响,把系统误差配准与融合检择结合起来研究,将融合检择中的异常测量视作系统误差配准中的离群点,只有当某设备与基准设备的测量数据同时通过检择时,该设备才进行系统误差配准更新。
4.2.3 样本大小和时变因素的考虑
当系统误差在总误差中所占的比例不超过5%时,可以认为消除了系统误差,而系统误差的估计精度与样本大小的平方根成反比(原文指均值估计,中值估计中同样应有样本越大,估计精度越高)。因此,配准时用于相对系统误差估计的样本大小应不小于400。初始化时,可以选择较少的样本计算出一个初始的配准值,融合过程中,逐步增加样本,提高配准精度。另一方面,本文方法在用于时变系统误差实时配准时,样本容量过大又会导致配准值出现较大偏差。因此,应根据实际情况选择大小适中的样本容量。

图2为基于融合检择与系统误差实时中值估计的配准算法主要流程。
5 测试与分析
5.1 与最小二乘法的比较
在A、B两雷达参加的某次动态测量中,将两雷达测量数据转至同一坐标系,分别用最小二乘法、改进的最小二乘法和中值法对其某一测量序列进行系统误差配准和融合检择,以更高精度的GNSS数据作为相对真值,检验融合效果。
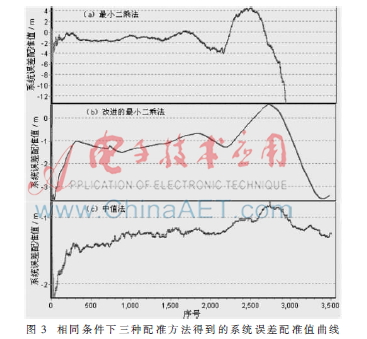
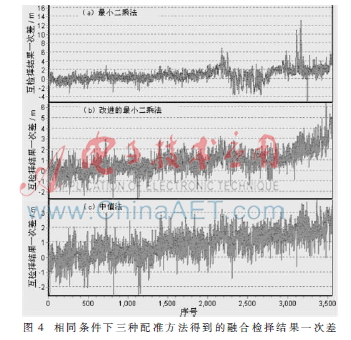
图3和图4给出了相同条件下,三种方法得到的系统误差配准值曲线和融合检择结果一次差。可以发现,采用最小二乘法进行系统误差配准时,由于其较易受到非假定误差的影响,在数据点3000附近,系统误差配准值出现了很大偏差,此后的融合检择结果受到严重影响,系统误差配准值也未再更新;改进的最小二乘法能够在一定程度上减小非假定误差的影响;中值法稳健性最好,无论是系统误差配准精度还是融合检择结果都较为理想。
5.2 在时变系统误差处理中的应用测试
在图4(c)中,可以看到明显的趋势项,这就是雷达测量数据相对于不同测量机制的GNSS测量数据的系统误差(主要为折射误差)随测量过程时变的表现。
前面提到,本文配准方法在用于时变系统误差实时配准时,应根据实际情况设定样本大小。为对选择不同大小样本容量时的系统误差配准结果进行比较,提出配准残差平均值的概念,即系统误差配准后用设备间一次差的平均值来表征设备间残留的相对系统误差大小。通过计算配准残差平均值,来比较算法在不同条件下的配准性能。
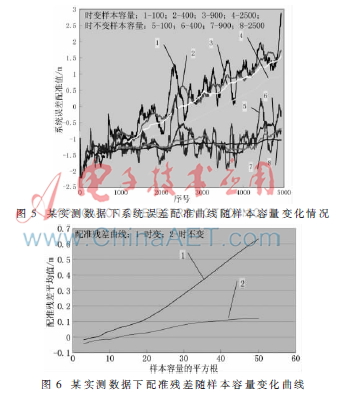
图5、图6为基于某实测数据的测试结果,选择适当的样本容量(400~900)时,本文方法在时变和时不变系统误差配准中都是适用的,其既能迅速收敛达到足够的配准精度,又能避免时变系统误差配准时发生大的偏差。
6 结束语
本文针对传统方法的不稳健性和复杂电磁环境对电子信息装备测量数据的影响,以稳健统计理论为指导,重点研究了中值估计在多源测量数据系统误差配准中的应用,提出的基于双向链表排序的系统误差实时中值估计算法以及与融合检择相结合的配准方法简明高效、稳健实用,在典型实测数据测试中达到了较好的稳健效果。
与文献[8]将联合航迹关联与系统误差估计结合起来研究、使用最小平方中值估计器完成系统误差的稳健估计相比,本文给出了选择基准设备、确定配准方案的参考原则,将融合检择与系统误差配准结合研究精度更高,采用设备间一次差的中值作为当前时刻设备间系统误差的估计值更为简明高效。同时本文提出配准残差的概念,丰富了配准算法测试手段,并对算法在时变系统误差配准中的应用进行了测试分析。
时变测试证明,选择适当的样本容量时,本文配准方法能够用于时变系统误差配准,这一定程度上也给出了一种有协同参考数据时折射误差、跟踪部位误差等时变系统误差分离、修正的参考方法。另一方面,本文提出的基于双向链表排序的实时中值估计算法也可用于稳健滤波之中,这将在以后的工作中进行相应的研究。
参考文献
[1] 廖海军,王卫星.一种多传感器配准与目标跟踪算法研究[J].电光与控制,2008,15(7):12-16.
[2] 刘德浩,王国宏,陈中华.基于EM-EKF的异类传感器系统误差配准算法[J].雷达科学与技术,2011,9(5):453-456,463.
[3] Zhou Y F.A kalman filter based registration approach for asynchronous sensors in multiple sensor fusion applications[C].Proceedings of the IEEE International Conference on Acoustics,Speech,and Signal Processing.Montreal.Quebec:IEEE press,2004,2:293-296.
[4] LEUNG H,BLANCHETTE M,HARRISON C.A least squaresfusion of multiple radar data[C].Proceedings of Radar.Paris.France:IEEE press,1994:364-369.
[5] ZHOU Y F,LEUNG H,YIP P C.An exact maximum likelihood registration algorithm for data fusion[J].IEEE T-SP,1997,45(6):1560-1573.
[6] 王波,王灿林,董云龙.RTQC误差配准算法性能分析[J].系统仿真学报,2006,18(11):3067-3069.
[7] 费业泰.误差理论与数据处理(第6版)[M].北京:机械工业出版社,2014.
[8] 田威,王钺,山秀明,等.稳健的联合航迹关联与系统误差估计[J].清华大学学报(自然科学版),2013,53(7):946-950.
[9] Roland Frieda,Thorsten Bernholtb,Ursula Gatherc.Compu-tational repeated median and hybrid filters[J].Statistics & Data Analysis,2006,50:2313-2338.

