摘 要: 在实时的交通路况中,路径规划的核心问题是快速而有效地找到从起点到达终点的最优路线。将PSO算法应用到的路径规划中来,针对实时变化的交通路况,在适应度函数中引入惩罚项来实现静态和动态下的路径规划,并通过引入变异算子的操作来避免该算法陷入局部最优。实验表明,改进后的PSO算法搜索效率高,时间开销随路网规模的扩大增幅较小,适用于大规模路网和动态路径规划。
关键词: 车载导航;路径规划;变异算子;局部最优
0 引言
路径规划是车载导航系统的基本功能,由于其有较强的应用价值,国内外学者对此进行了深入的研究[1-3]。现今较流行的算法有Dijstra算法(简称D算法)和A*算法,但D算法搜索速度较慢,A*算法搜索速度快但成功率不高,且这些算法只能在静态地图上进行路径规划,没有考虑实时变化的交通状况。近年来,智能算法因其强大的搜索能力而被广泛应用于路径规划中。杨易[4]把遗传算法与A*算法相结合,提高路径规划算法的效率;王健[5]把蚁群算法应用到导航的路径规划中,但其没有考虑随时间的动态变化因素;于海璁等人[6]提出了一种适用于多模式路径规划的遗传算法,可用于个性化的路径导航。本文将PSO算法应用到车载导航的路径规划中,引入变异算子解决PSO算法的局部最优问题,不仅拥有较快的收敛速度,还能增强全局搜索能力。
1 粒子群算法的描述
粒子群算法由Eberhart博士和Kennedy博士在1995年提出[7],它通过粒子间的协作和信息共享来寻找最优解。算法在搜索时,根据粒子自身历史的最佳位置pbest和种群内所有粒子历史的最佳位置gbest的基础上进行位置变化,其速度和位置公式如下:

其中,t表示迭代次数,r1、r2是(0,1)之间的随机数,c1、c2为学习因子,w为惯性权重,其表达式为:

其中wmax、wmin为权重的最大和最小值,tmax为最大迭代次数。
2 粒子群算法在路径规划中的应用
本章节的主要内容是解决粒子的编码和适应度函数的构造,编码方式涉及粒子位置和速度的更新操作,适应度函数用来评价粒子的适应值。最后还解决了PSO算法自身陷入局部最优的问题。
2.1 粒子编码
编码即粒子位置的表达方式,是设计粒子群优化和应用操作的关键问题,根据路径规划的实际情况,本文采用直观、方便的实数编码[8]。粒子状态表达方式如式(4)所示,编码方式如式(5)所示。
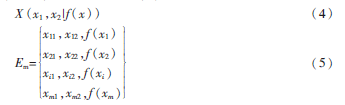
其中,f(x)表示适应值,m表示粒子个数。
2.2 适应度函数
2.2.1 适应度函数的设计
将粒子群算法用于路径规划时,适应度函数的设计使得该算法不仅能够在静态网络下获得最优路径,通过增加惩罚项M[9]也能适用于实时变化的交通状况,其适应度函数定义为:

(1)当0<n<0.5时,畅通;
(2)当0.5≤n<0.75时,微拥挤状态;
(3)当0.75≤n≤1时,严重拥堵状态。
针对不同的拥堵状态采用不同的适应度函数。
适应度函数主要取决于是否有交通拥堵等状况,车载导航仪[10]将接收到的交通信息转换成路段的相关特性数据,同时给出交通拥堵系数n,并根据n的大小选择相应的适应度函数。采用该适应度函数的优点是占用的存储空间少,并根据实时的交通状况找出最佳路径。
2.2.2 适应度函数对路径规划的影响

如图1所示,粒子群的起点为S,终点为D。粒子群从S点开始搜索,若不定义适应度函数,则粒子随机选择移动方向,而根据适应度函数(式(6)),大部分粒子选择更靠近终点的右方,小部分粒子选择左方,如图1(a)所示。当粒子到达下一路口时,重新计算自身适应值,并共享当前全局最优解,各个粒子根据式(1)、(2)更新自身的速度与方向。因此,在单位时间段内,沿着上方行走的粒子数量高于其他方向的粒子数,同时这些粒子记录自身的局部最优解,也能得到全局最优解。后续粒子选择路径时会受这些最优解的影响,沿着粒子较多的方向前进,也有小部分粒子会选择其他方向来寻求更短的路径,如图1(b)所示。当某个粒子到达终点时,其他粒子将会收到该粒子共享的信息,所有粒子将会朝该方向前进,如图1(c)所示。
2.3 解决陷入“局部最优”的问题
为了避免PSO陷入“局部最优”,本文在PSO算法中引入变异算子,其思想是:当算法达到特定的迭代次数h之后,除去之前拥有全局最优解的粒子外,计算其他粒子与当前全局最优值gbest的距离,若距离小于阈值,则取这些粒子的百分比重新初始化,使这部分粒子重新寻找最优值,使种群获得更高的粒子多样性,扩大搜索范围,避免粒子群算法陷入局部最优,同时能够增强全局搜索能力。带变异算子的粒子群算法如下:
If(t<tmax&&>h)
取满足dp-gbest<DistValue粒子中的百分比,并根据式(1)、(2)对其速度与位置进行重新初始化;
Else
按式(1)、(2)更新粒子速度和位置;
End
其中,t为当前迭代次数,tmax为最大迭代次数,h为特定的迭代次数,dp-gbest表示粒子的当前点到全局最优解gbest的距离,DistValue为设定的距离值。
3 算法验证与分析
为了验证上述算法的可行性,本文根据上海市松江区部分实际地图抽象得到的路网数据结构进行实验,如图2所示。

其中路段数为134,路口数为92,粒子数为95,最大迭代次数为200,wmax=0.9,wmin=0.4,c1=c2=2。最优路径标准采用最短路径,PSO算法的路径规划结果如图3所示,D算法路径规划的结果如图4所示。
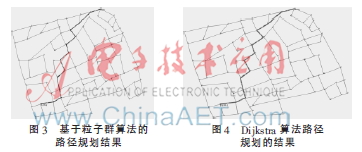
由图3和图4可知,D算法规划出的最优路径与粒子群算法的最优路径是一样的,但两个算法的搜索时间不同,D算法搜索时间为46 ms,粒子群算法搜索时间为55 ms。
上述结果是在实际地图上进行的小规模节点数的实验,图5和图6是对大规模节点数进行仿真的结果比较。

由图5可知,PSO算法和D算法在节点数相当的情况下,算法求得的路径长度是相同或相似的,但由图6可知,由于D算法与PSO算法的原理和收敛方式不同,在节点数目较少时,PSO算法需要更多的时间,但是随着节点数目的增加,PSO算法的收敛速度较D算法明显要快,在大规模路网中,PSO算法具有较大优势。

最后当在路段中设置严重交通拥堵,即0.75≤n≤1时,其路径规划的结果如图7所示。
由图7可知,当在道路上设置拥堵路段时,算法重新规划出了一条避开拥堵路段的最优路径,相比于只能够运用在静态路网的D算法,该算法更具有实际意义。
4 结论
本文将粒子群算法用于路径规划中,从粒子的编码规则到适应度函数的设计,再到解决局部最优问题等,充分体现了本文的创新性技术,为路径规划算法提供了新的研究思路。实验结果表明,该算法切实可行,其搜索效率高,时间开销随路网规模的扩大增幅较小,适用于大规模路网,同时在实时变化的交通路况中更具有实际意义。
参考文献
[1] 岳双.动态路径规划算法在车辆导航领域中的应用[J].数字技术与应用,2012(3):95-96.
[2] 殷超.基于改进Dijkstra算法的最短路径搜索仿真[J].山东理工大学学报(自然科学版),2011,24(6):33-36.
[3] 张仁平,周庆忠,熊伟,等.A*算法改进算法及其应用[J].计算机系统应用,2009(9):98-100,107.
[4] 杨易.智能车辆组合定位与路径导航技术研究[D].长沙:湖南大学,2007.
[5] 王健.基于蚁群算法的车辆导航自适应路径规划算法研究[D].青岛:青岛科技大学,2011.
[6] 于海璁,陆锋.一种基于遗传算法的多模式多标准路径规划方法[J].测绘学报,2014,43(1):89-96.
[7] 唐小勇,于飞,潘洪悦.改进粒子群算法的潜器导航规划[J].智能系统学报,2010,5(5):443-448.
[8] 史辉.车载导航路径规划算法研究[D].郑州:解放军信息工程大学,2010.
[9] 李淑红,张巧荣.二进制粒子群算法在路径规划中的应用[J].计算机工程与设计,2009,30(21):4953-4955.
[10] 孙海鹏,翟传润,战兴群,等.基于实时交通信息的动态路径规划技术[J].微计算机信息,2007,23(8-3):177-178.

