代曦,李骞,顾大权,黄岩
(解放军理工大学 气象海洋学院,江苏 南京 211101)
摘要:等值线编辑是对各形势场等值线自动化分析结果的人工修正,是对提取准确等值线结果的必要补充。针对已有等值线交互编辑方法难以满足不相交约束、操作复杂等问题,提出一种基于拉普拉斯坐标系的等值线交互编辑方法。实验结果表明,编辑结果有效保持了原有等值线的形状拓扑,且人工操作更少,可满足业务应用中等值线交互编辑需求。
关键词:等值线; 三角剖分;拉普拉斯
0引言
*基金项目:国家自然科学基金项目资助(41305138,41174164)等值线是将数据某一数量指标值相等的各点连成的平滑曲线,它具有连续性、不相交等特点。现有等值线分析主要分为手工分析和软件自动分析两种,其中手工分析相对复杂、耗时较长,但此方法优势在于可融合预报人员经验与其气象要素信息;自动分析采用网格追踪等方法对格点数据进行跟踪,分析速度快,但与手工分析结果存在一定差距,不能很好地满足业务需求。当前大多数可视化及气象分析软件已实现等值线的自动分析功能,SURFER、Micaps、Grads、MATLAB、ARCGIS、Tecplot等均有等值线分析模块[12]。上述系统的主要问题表现在:订正结果不能满足等值线网格局部的拓扑结构需求;修正等值线时容易出现等值线相交的情况;只能实现对单条等值线进行修改,如对多条线进行修改,需要反复操作,效率低。
针对上述问题,本文提出了一种基于拓扑结构的等值线修正方法。首先对已有的等值线数据进行三角剖分,依据剖分结果识别等值线间的拓扑关系,并对剖分结果建立Laplacian坐标系[34]。然后由用户交互输入修改意图,在交互修改过程中通过Laplacian坐标对等值线修改移动部分进行约束,同时通过笛卡尔坐标约束固定点,通过最小二乘法求解移动点和固定点双重约束下的线性系统,从而重新修改移动点[56]。通过上述方法,可以实现在保持等值线集合拓扑结构的前提下对等值线进行修改。
本文提出方法的流程如图1所示。

1三角剖分
三角剖分是计算机辅助几何设计、几何造型及计算机图形学中研究的重要内容之一。本文将等值线集合进行离散化并对得到的离散点进行三角剖分得到三角网格。目前,三角剖分可以通过动态规划[7]和德劳内三角剖分算法[8]实现,但动态规划算法主要是通过计算最短边来排除病态的三角网格。而在等值线族中,由于等值线弯曲变化,部分等值线在某一个区域内较为集中,通过动态规划算法来实现三角剖分可能丢失等值线间的拓扑关系。因此,本文采用德劳内三角剖分算法。其主要流程如图2所示。
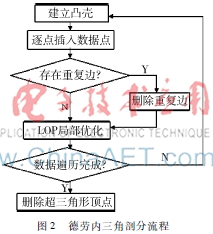
首先建立凸壳,包含了所有的离散点,然后向其中插入一点,该点与包含它的三角形三个顶点相连,形成三个新的三角形,然后逐个对它们进行空外接圆检测,同时用Lawson设计的局部优化过程LOP进行优化,即通过交换对角线的方法来保证所形成的是Delaunay三角网。
2拓扑结构识别与Laplacian坐标系建立
Laplacian坐标表示方法又称为微分坐标方法或δ坐标[9],或局部平均曲率法线。在网格顶点处应用Laplacian算子,可用于表征局部曲面的几何特征。建立拓扑结构后,将笛卡尔坐标系转换为差分的拉普拉斯坐标系。主要针对修改范围内的点,为下一步能量方程求解提供依据。
根据设定的修改范围,从用户选中的坐标点出发,广度搜索出一系列邻接点,根据差分坐标公式求出每点的δ坐标。得到的坐标存储在链表中。本文为了建立拉普拉斯坐标系进行如下定义:
(1)拉普拉斯网格

μ表示已知的N个点组成的三角网格。V表示节点,E表示边,F表示平面。每个i∈μ表示笛卡尔坐标系中的节点用vi=(xi,yi,zi)表示。
首先通过中心和与它直接相连的节点定义差分坐标系:

其中,N(i)={j|(i,j)∈E},表示与i节点相邻节点的个数。
从绝对笛卡尔坐标系到差分坐标系的转换可以表示为一个矩阵:

令D是一个对角阵,Dii=di,矩阵从绝对坐标系转换到关系坐标系:
L=I-D-1A(4)
定义:
Ls=DL=D-A(5)
那么,

Lsx=Dδ(x),Lsy=Dδ(y),Lsz=Dδ(z)
其中x是n个向量包含x的绝对坐标的所有顶点。
矩阵Ls被称为拓扑拉普拉斯网格。图形表示的拉普拉斯广泛地应用在代数和图形学原理中,最主要的原因是因为它的代数特性能很好地与图形表示相结合。从差分几何角度来看,δ坐标系被视作离散化的连续拉普拉斯贝尔特拉米算子。

(2)三维仿射变换
常见的三维变换包括平移变换、旋转变换、缩放变换、反射变换和错切变换。若取齐次坐标来表示三维空间中的点,三维变换可表示为4×4的变换矩阵。
记(Tx,Ty,Tz)为平移向量, 绕x轴旋转θ角的旋转变换矩阵为:

同样可以获得绕y轴、z轴旋转的变换矩阵。缩放矩阵为:
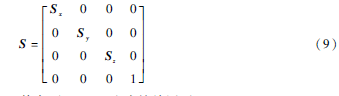
其中,(Sx,Sy,Sz)为缩放因子。
3能量方程的求解
通过网格模型的笛卡尔坐标构造其Laplacian坐标。由于变换矩阵L(或Ls)为奇异矩阵[10],不存在可逆矩阵,因此不能使用V′=L-1δ重建模型。
由于Laplacian坐标存在平移不变性,因此变换矩阵L的秩为n-1。为了能够唯一地重构笛卡尔坐标系中的网格模型,需要求解一个满秩的线性方程组,因此需要指定更多的变形特征顶点的笛卡尔坐标为约束条件。令空间中位置已知顶点的索引值集合为C,有|C|个位置约束的形式为:
V′j=cj,j∈C
如果记C={1,2,...,m},则需要求解的线性方程组表示如下:

方程组中的系统矩阵记为Lo。在本文中,使用公式作为位置约束条件(或称为模型约束条件)。权值ω>0可以用来调整位置约束条件的重要性,每个约束都应该有相应的权值,可以在Laplacian矩阵上针对不同行使用不同的权值。附加的属性约束条件使线性方程组成为超定方程组,因此基本上没有完全精确的解,可通过最小二乘法求解近似解,当系统满秩时就存在唯一解:

式(11)的第一项表示尽可能保持原始网格的Laplacian坐标不变,第二项表示尽可能减少特征顶点处的误差。求解值的精确度与现行方程组的约束条件有很大关系。
基于线性边约束的网格编辑方法在模型重建时,通过最小二乘系统求解获得的模型为近似解。当模型集合细节特征较复杂时,一次求解不一定能获得较高质量的变形效果,需要多次迭代求解,逐渐逼近精确值。
4实验结果与分析
为了验证方法的可行性,本文分别使用仿真数据和2011年数据库中选取的4月20日12时的全球等压线数据进行了实验。仿真数据为16条平行线,共510个采样点。全球等值线数据共有682条等值线,19 985个采样点。
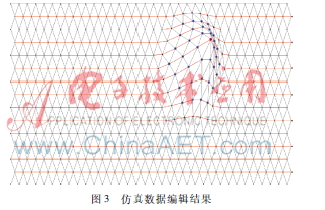
图3仿真数据编辑结果通过上文提到的两个过程,用户交互编辑修改点,使其带动修改范围内的点一起移动,从而达到修改的效果,实验结果如图3。其中用户交互修改的点只有浅色的点,深色的点均根据浅色点移动而改变位置,从而达到等值线修改范围内自动编辑的要求。
本文对全球数据的局部进行编辑实验,根据修改范围不同编辑结果如图4。图4的修改范围为2个网格。

从实验结果可以看出,不同的修改范围得到的数据编辑结果是不同的。最后本文对全球数据进行了编辑实验,如图5所示。其中用户选择的修改范围在左下角。
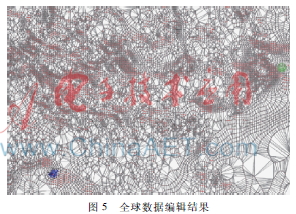
实验结果证明,采用本文方法对等值线数据进行局部自动修正是可行性的。
参考文献
[1] 王软宏. 等值线的自动绘制方法及在计算机上的实现[D].吉林:吉林大学数学研究所,2003.
[2] 中国气象局.MICAPS3.2 用户使用手册[Z]. 2012.
[3] SORKINE O, LIPMAN Y, COHENOR D, et al. 2004.Laplacian surface editing[C]. In SGP′04: Proceedings of the 2004 Eurographics/ACM SIGGRAPH Symposium on Geometry Processing, ACM, New York, USA:175184.
[4] LIPMAN Y, SORKINE O, COHENOR D, et al. Differential coordinates for interactive mesh editing[C]. In Proceedings of Shape Modeling International (2004), IEEE Computer Society Press:181190.
[5] BOTSCH M, BOMMES D, KOBBELT L. Efficient linear system solvers for mesh processing[J]. IMAMathematics of Surfaces XI, Lecture Notes in Computer Science,2005,3604:6283.
[6] FLOATER M S. Mean value coordinates[J]. Computer Aided Geometric Design, 2003,20(1):1927.
[7] 刘晶, 张九龙, 李晔, 等. 基于图像不变特征与三角剖分的水印算法[J]. 西安理工大学学报, 2009, 25(2): 227230.
[8] 余杰, 吕品, 郑昌文. Delaunay 三角网构建方法比较研究[J]. 中国图象图形学报, 2010, 15(8): 11581167.
[9] 许斌,李忠科,宋大虎.基于支持向量机的 Laplacian 网格曲面孔洞修补算法[J].计算机工程与设计, 2014, 35(1): 237242.
[10] 王勇.基于流形学习的分类与聚类方法及其应用研究[D].长沙:国防科学技术大学, 2011.

