摘  要： 提出了一种用Surfer软件提供的可编程方法对散点数据进行网格化，再用矩形追踪法追踪等值线的新方法。利用新方法绘制出的等值线既具有高精度性和实用性，又具有可维护性，这也表明该方法是一个实用、有效的等值线绘制方法。
关键词： Surfer；等值线；离散数据网格化；矩形追踪

　等值线图是在石油勘探开发、采矿、地质、地球物理、地球化学和气象等工程和技术领域内应用极广的一种图形，是众多领域成果表示的重要图件之一。在等值线绘制过程中，首先要对散点数据进行网格化，而常用的数据网格化方法（如距离加权法、方位法、趋势面法、加权最小二乘法、叠加法）的精度和有效性都不高；Kriging估值技术虽然比传统的估值技术具有更高的先进性和有效性，但这种方法目前还没有得到广泛应用，许多细节问题还处于研究阶段。本文介绍利用Surfer软件提供的可编程方法对散点数据进行网格化，然后用矩形追踪法对网格化后的数据进行追踪，并实现了放大、缩小、漫游、光滑等功能，绘制出的等值线具有更强的实用性。
1 绘制等值线图原理
1.1 离散数据网格化
　为了绘制等值线图，首先需要把离散分布的数据点网格化。为此，要建立数字高程模型（DEM），其主要功能就是将离散数据网格化。其主要步骤为：首先，由原始数据点的横、纵坐标的最小值和最大值构成矩形网格的边界；然后，根据用户需要将矩形再划分为m×n个小矩形，即形成矩形网格；最后，用插值算法得到每个网格点的高程值。
　DEM内插有多种算法，常用的有距离加权法、样条函数内插、最小二乘配置法和Kriging方法等。本文使用Suffer软件中提供的可编程方法对散点数据网格化，其具体算法如下。
　（1）输入参数；
　（2）根据输入参数从数据库提取X、Y坐标及高程值Z，并保存到文本数据文件；
　（3）在程序中引用surfer并创建surfer（srf）和grid（grd）对象；
　（4）用srf对象的GridData方法将文本文件转换成surfer格式文件（.grd文件）；
　（5）用grd对象的GetNode方法获取grd文件里生成的网格点高程值，写入网格化后的数据文件。
1.2 等值点的计算
　令任意一个网格边两端的数据值分别为Z1、Z2，如图1所示，对于任意一条等值线W，它在该边上Z（x，y）-W=0，即等值线所通过的点，可以有0~3个根。

　当等值线恰好等于网格节点的值时，这种网格点被称作退化点，当遇到退化点时，在网格点值上加上一个非常小的正数，以消除退化点[3]。
　如图1中的Z1、Z2值都不会等于等值线W的值，这时，网格边上对于某一条等值线W，存在根Z（x，y）-W=0的可能性有：
　（1）Z1>W，Z2>W或Z1<W，Z2<W时，没有根，如图1中的（a）和（b），或存在两个根，如图1的（e）和（f）。
　（2）Z1<W，Z2>W或Z1>W，Z2<W时，存在一个根，如图1中的（c），或存在两个根，如图1中的（d），其中A根是重根，如图1中的（g）。
　对于立方函数，利用数值法求根。这时可以将网格边长nx和ny再分成等间距的细分段，如图1中的（d）所示，然后求出每个细分段两端的函数值Zk和Zk+1。当Zk或Zk+1等于等值线值W时，同样需要加上一个非常小的正数，以消除退化点。这样，当（Zk-W）（Zk+1-W）<0时，说明该细分段上存在一个根。该细分段的长度可以小到以机器步长来计算，最小可以到描绘仪机器步长的2倍，这样可以保证在曲面函数上追踪所得到的等值线连续光滑而不会发生方向上的突变。在找到根值的细分段上，再以Zk和Zk+1作线性内插求得所在根及等值点的位置。
　数值法找根时有时会失根，尤其对于重根情况，如图1（d）中的A根，由于它两端的Zk和Zk+1都小于W，因此（Zk-W）（Zk+1-W）>0，A根就会失去，但这对于绘制等值线并无多大妨碍，至多漏绘一些极小的封闭等值线或等值线应该封闭而不完全封闭。
1.3 等值线的追踪
　把网格纵边和横边的细分段所组成的小网格称为单元，它们的4个节点称为单元节点，以区别于原始的网格与网格节点。这样，对于每一个单元在其单元节点上求出函数值后（若遇到有退化点时，同样需要通过加一个很小的正数来处理），有图2所示的8种连接等值线的可能（其中+号表示节点值大于等值线值，-号表示节点值小于等值线值）。
　（1）单元节点上函数值同时大于或同时小于等值线值时，该单元内没有等值线通过，如图2（a）所示。
　（2）单元节点上函数值大于和小于等值线时，单元边上要么存在两个根，要么存在4个根。存在两个根时，两根在对边上，如图2（b）、图2（c）所示，两根在邻边上，如图2（d）、图2（e）、图2（g）、图2（h）所示；存在4个根时，4个根分别在单元的4个边上。对于两个根的情况，只要找到根的位置就可以相连；对于4个根的情况，则需规定底边根与左边根相连，右边根与上边根相连或底边根与右边根相连，右边根与上边根相连，如图2（f）所示，这样就能保证等值线间不会出现相交现象[4]。

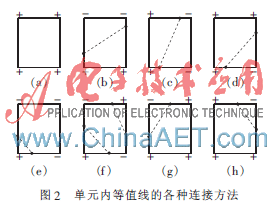
　图3表示在一个矩形网格（i，j）内，将纵边ny等分成6个细分段，将横边nx等分成5个细分段的连法示意图。在等分后的每个单元节点上算出函数值Z。Z>W（W为等值线值）时，以“+”表示；Z<W时，以“-”表示。这样在每个“+”、“-”节点之间必定存在一个等值线根，可用线性内插求出它的位置，连成的等值线如图3中的折线所示。由于网格边上的函数是立方函数，它在网格边上最多有3个根，如图3中，底边上有3个根A1、A2、A3。在理论上只要对全部网格内的单元节点扫描一遍，把求得的根值用图2中的规则相连即可画出等值线图。

　但是这样计算会花费计算机大量时间，而且大部分单元内是不会有等值线通过的。因此，需要设计一种总等值线的方法，使得只在等值线会通过的单元节点上才求出函数值，而大部分不通过等值线的单元不必求节点函数值，以节省机器运算时间、加快速度。这里还需指出，图3是一个复杂化的例子，实际上，对于特定的等值线，一个网格内的等值线可能是很少的，或者只有一条或少数几条，还有很多网格根本就没有。此外，当分段加密时，等值线将逐渐变成光滑曲线，这是因为拟合网格点的函数是一个连续光滑的函数。因此，利用上述方法，就不需要对等值线再作光滑处理。
将等值线分为从边界出发到边界结束的等值线以及在内部封闭的等值线两种类型，如图4所示。无论哪种类型的等值线，都必须已知有顺序相邻的A1、A2两个等值点。设它们的坐标值分别为（a1x，a1y）及（a2x，a2y），分别以nx和ny为单位长度，其坐标的整数值为（a1j，a1i）及（a2j，a2i）。任意设两个相邻的单元如图5中的单元Ⅰ、Ⅱ所示，A2落在单元Ⅰ和Ⅱ的邻边上，A1落在单元Ⅰ的其他三边的任意一边上。用（i，j）表示单元Ⅰ的序号，用（i+1，j）、（i，j+1）、（i-1，j）、（i，j-1）表示单元Ⅱ的序号，分别相当于图5中的（a）、（b）、（c）、（d）4种情况，则下一等值点追踪方向依次由下述4个判别式确定。

　
　 
　网格追踪程序主要封装在CContourTrace类中。
　利用本文方法所生成的等值线如图6所示。

　本文是提出了一种新的方法来实现等值线的绘制，它首先用成熟软件Surfer将原始数据进行网格化，再利用矩形网格追踪法追踪网格，并按照实际需求实现了对等值线的缩放、平移、光滑和标注等功能。利用本方法所绘制的等值线主要在石油勘探开发、采矿等领域得到应用。使用本方法所绘制的等值图较其他方法效果更好、精确度更高、速度更快，是一个实用有效的等值线绘制方法。
参考文献
[1] 王永会，宋晓宇，栾方军．基于网格的等值线图快速生成算法[J]．计算机工程与应用，2001（17）：124-125.
[2] 陈学工，刘凯敏．一种基于格网法快速生成等值线的算法[J]．电脑与信息技术，2007，15（3）：4-6.
[3] 宋丽娟，龚晓峰，钟猛．基于网格法的等值线绘制方法[J]．现代电子技术，2005，28（14）：65-67.
[4] 韦美雁，杜丹蕾．基于规则网格的等值线的生成研究[J]．湖南科技学院学报，2007，28（4）：39-41.
[5] 于嘉，吴旭．一种改进的矩形网格等值线追踪算法[J]．河南师范大学学报，2008，36（6）：34-36.
[6] 张利，王俊彪，张贤杰．基于矩形网格追踪法的曲面主曲率等值线生成算法[J]．计算机应用研究，2009，26（8）：3179-3181.