张任

　　（浙江师范大学 数理与信息工程学院,浙江 金华 321004）

　　摘要：数据流挖掘是当前数据挖掘研究的一个热点，并且数据流的类型也不尽相同。利用模糊粗糙集和F-粗糙集的基本原理和基本方法，提出了一种对模糊型数据流进行模糊并行约简、删除冗余属性的方法，并运用模糊并行约简中属性重要性的变化探测模糊概念漂移现象。有别于传统方法，该方法利用模糊数据的内部本质特性对模糊概念漂移进行探测，并且通过实例验证其探测模糊概念漂移的可行性和有效性。

　　关键词：模糊数据流；概念漂移；模糊粗糙集；F-模糊粗糙集；模糊并行约简

0引言

　　信息爆炸的今天,现实中的数据往往随着时间的变化而变化，例如，电商销售数据、微博数据、传感器数据等，这种类型的数据称为数据流［1］。数据流具有按照时间顺序排列、快速变化、连续、海量甚至无限且可能出现概念漂移现象等特征［2-3］。探测概念漂移常用的技术是滑动窗口技术［1］。参考文献［4-6］对单个的数据块或单棵决策树进行冗余属性删除，没有从整体上考虑删除冗余属性问题，再检测概念漂移。参考文献［7］从整体上考虑删除冗余属性问题，但是未能解决数据流中模糊属性约简问题。

　　粗糙集理论［8］是一种处理不相容、不精确或不完全数据的强有力工具。模糊粗糙集是粗糙集理论的扩展研究，它解决了粗糙集约简处理之前必需的离散化过程，使得粗糙集也适用于模糊概念和模糊知识的属性约简。基于模糊粗糙集的属性约简取得了一定的研究成果［9-12］。传统的模糊粗糙集理论不太适合研究海量的、动态变化的数据，也不太适合研究数据流；F-粗糙集［13-14］将粗糙理论从单个信息表或决策表推广到多个，适合研究海量的、动态变化的数据，也适合研究数据流,F-模糊粗糙集［15］是该理论的扩展研究。模糊并行约简是与F-模糊粗糙集合相对应的属性约简理论和方法。模糊并行约简和F-模糊粗糙集比较适合研究海量的、动态变化的数据，也应该能够研究模糊数据流和模糊概念漂移。

　　本文首先利用F模糊粗糙集的模糊并行约简理论，将模糊数据流的各个滑动窗口(子决策表)中对分类不起作用的冗余模糊属性整体删除，然后运用各个子表(滑动窗口)中属性重要性的变化探测模糊概念漂移。传统方法主要依靠分类准确率的变化利用外部特性进行比较，探测概念漂移现象。本文方法与传统的概念漂移探测方法不同，利用数据的内部特性——模糊并行约简后属性重要性的变化探测模糊概念漂移现象。

1基础知识

　　本节介绍F-模糊粗糙集和模糊并行约简［15］的基础知识。本文若未特别说明,属性均表示模糊条件属性。

　　下面用FIS={ISi}(i=1,2,…,n)表示与模糊决策系统簇DS=(U,A,d)相对应模糊信息系统簇，A是条件属性集,d是决策属性集，且属性对应的是模糊等价关系(或简写为关系)。其中ISi=(Ui,A)，而DSi=(Ui,A,d)。在模糊子信息表ISi中,设P是论域U的一个模糊等价关系（简写为关系P），Eij是属于UiP的模糊等价类,UiP=GD(P|Ui)={Ei1,Ei2,…,Eici} 表示论域Ui上的一个模糊划分(j=1,2,…，ci,ci是由p划分论域Ui所得模糊等价类的数目)。

　　定义1在信息系统簇FIS中,模糊概念X在关系P下的模糊粗糙上下近似(简写为上下近似)分别为：

　　下近似:μFISX(x)={μPX|U1(x),μPX|U2(x),…,μPX|Un(x)}

　　上近似:μFISX(x)={μPX|U1(x),μPX|U2(x),…,μPX|Un(x)}

　　序偶(P(FIS,X),P(FIS,X))称为F模糊粗糙集。

　　如果P(FIS,X)=P(FIS,X),则称序偶(P(FIS,X),P(FIS,X))是精确的。

　　定义2在ISi中条件属性的模糊等价类E的模糊正域为：

　　μPOSP(d)(E)=supqj∈U/dμqj(E)

　　x对模糊正域的隶属度为：

　　μPOSP(d)(x)=supx∈Uimin{μE(x),μPOSP(d)(E)}

　　其中,j={1,2,…,cj}，cj是由d划分论域U所得模糊等价类的数目,E∈GD(P|Ui)。

　　定义3设DS=(U,A,d)是一个决策系统，P(DS)是DS的幂集，FP(DS)，则PA称为F模糊并行约简，当且仅当PA满足下面条件：

　　(1)μPOS(F,A,d)=μPOS(F,P,d)；

　　(2)对任意SP，都有μPOS(F,S,d)≠μPOS(F,A,d)。

2模糊并行约简方法对概念漂移的探测

　　在F-模糊粗糙集［15］中决策子系统簇F中的元素可以是大数据中的一部分，也可以是模糊数据流中的一部分或是一个滑动窗口。本文假设模糊决策子系统簇F中的元素是数据流中的一部分，每一个子表可以看做一个滑动窗口。在探测模糊概念漂移之前，先用模糊并行约简算法删除对分类不起作用的冗余模糊属性，以减少计算量，并探测真正使模糊概念发生漂移的属性之变化。

　　2.1模糊并行约简算法

　　在F-模糊粗糙集中依赖度与属性重要性的定义如下［15］。

　　定义4在FIS={ISi}(i=1,2,…,n)中决策属性对条件属性集P的依赖度为：

　　定义5给定一个决策子系统簇F,DTi=(Ui,A,d)∈F(i=1,2,…,n),定义F中属性a∈P或a∈A－P相对于P的重要度分别为:

　　σ(P,a)=γ(F,P,d)－γ(F,P－{a},d)或σ′(P,a)=γ(F,P∪a,d)－γ(F,P,d)

　　运用属性重要度可以比较容易地求出并行约简，算法如下。算法1基于F模糊属性重要度的模糊并行约简算法(简称FPRAS)输入：FP(DS);

　　输出：F的一个模糊并行约简;

　　（1）P=;

　　（2）对于任意a∈A,如果σ(A,a)>0,那么P=P∪{a}；

　　（3）M=A－a；

　　（4）重复进行如下步骤,直到M=:

　　①对任意a∈M,计算σ′(P,a) //σ′(P,a)=γ(F,P∪a,d)－γ(F,P,d);

　　②对任意a∈M,如果σ′(P,a)≤ξ//1>ξ≥0为给定的阈值，那么M=M－{a};

　　③选择F属性重要度非零且最大的元素a∈E,P=P∪{a},M=M－{a}(添加属性集M中F属性重要度非零且最大的属性到并行约简P中);

　　（5）输出并行约简P。

　　2.2模糊概念漂移探测

　　通过模糊并行约简删除了数据流中对分类不起作用的冗余模糊属性。受参考文献［7，1314］中属性重要性矩阵的启发，建立数据流约简后的属性重要性矩阵，用于描述在不同的模糊决策子表(滑动窗口)中模糊并行约简中的每个模糊属性对分类的贡献，它的定义如下。

　　定义6DS=(U,A,d)是一个模糊数据流决策系统，P(DS)是DS的幂集，FP(DS)是数据流DS=(U,A,d)的若干个滑动窗口的集合，PA是F的模糊并行约简，模糊并行约简PA关于F的属性重要度矩阵定义为：

　　根据属性重要性矩阵的定义，很容易证明属性重要性矩阵的下列属性。

　　定理1模糊数据流决策子表簇FP(DS)中，PA为并行约简，模糊属性重要性矩阵T(P,F)中的元素与模糊属性重要性矩阵T(A,F)中相应的元素有如下关系：

　　（1）若属性p∈PA为模糊并行约简的核属性，则p在T(P,F)中对应的元素值小于等于p在T(A,F)中对应的元素值。

　　（2）若属性p∈PA为模糊并行约简的非核属性，则p在T(P,F)中对应的元素值大于等于p在T(A,F)中对应的元素值。

　　推论模糊数据流决策子表簇FP(DS)中，PA为模糊并行约简，属性重要性矩阵T(P,F)中非零元素的个数大于等于T(A,F)中非零元素的个数。

　　运用粗糙集理论对概念漂移进行度量的指标［1617］往往依赖于上下近似，这种度量不太适合大小不一致的滑动窗口。参考文献［7］的并行约简探测算法不适合探测模糊型数据流的模糊概念漂移问题。下面运用属性重要性的变化对模糊概念漂移进行度量，它独立于上下近似的变化，也独立于滑动窗口的大小。它的定义如下。

　　定义7模糊数据流决策子表簇FP(DS)中，PA为模糊并行约简，两个滑动窗口DTi、DTk∈F相对于属性b∈PA的概念漂移定义为：

　　FPRCDb(DTk,DTi)=|σkj－σij|

　　其中，j为属性b∈PA在T(P,F)中所对应的列。

　　定义8模糊数据流决策子表簇FP(DS)中，PA为模糊并行约简，DTi、DTk∈F,基于模糊并行约简PA的模糊概念漂移量定义为：

　　FPRCDP(DTk,DTi)=1|P|∑|P|j=1|σkj－σij|

　　定理2基于模糊并行约简的属性重要性的模糊概念漂移量FPRCDb(DTk,DTi)和FPRCDp(DTk,DTi)对称、非负、满足三角不等式。

　　定理3模糊数据流决策子表簇FP(DS)中，DTi，DTk∈F,PA为模糊并行约简，则T(P,F)中相邻两行对应属性重要性变化的元素个数大于等于T(A,F)中相邻两行对应属性重要性变化的元素个数。

　　定理1、定理3说明冗余属性的存在干扰了概念漂移的探测，删除了一些冗余属性后模糊概念漂移更明显。下面利用基于模糊并行约简的模糊概念漂移量来探测概念漂移。算法2模糊概念漂移检测算法输入：模糊数据流FP(DS)，阈值δ;

　　输出：模糊数据流FP(DS)中是否发生概念漂移;

　　(1)调用算法1，求出F的模糊并行约简PA；

　　(2)计算约简后F中各个模糊属性的重要性，形成模糊属性重要性矩阵T(P,F)；

　　(3)计算相邻两行之间任意模糊属性重要性的差异FPRCDb(DTk,DTi)，并算出FPRCDP(DTk,DTi)；

　　(4)模糊概念漂移值FPRCDb(DTk,DTi)、FPRCDp(DTk,DTi)与给定的阈值δ比较，判定是否发生了概念漂移。

　　阈值δ∈［0,1)的最优选取将是下一步的研究方向。通过算法2可知,模糊并行约简将模糊决策子表簇作为一个整体考虑，删除了模糊决策子表簇中对分类不起作用的冗余属性，使得在模糊概念漂移的探测和分类的时候减少了计算量，并将注意力真正集中到对分类起关键作用的属性集合上。基于模糊并行约简探测概念漂移时，提供了同样的模糊属性和同样的标准，得到结论的可理解性与可靠性就会更加可信。

　　例1模糊决策系统DS=(U,A,d)(如表1所示),U={1,2…,10}为论域,P1、P2、P3为模糊条件属性,d为模糊决策属性。F={DSi}(i=1,2)是DS的模糊决策子系统 ,FIS={ISi}(i=1,2)是与F相对应的模糊决策系统簇，如表2、表3所示。　　

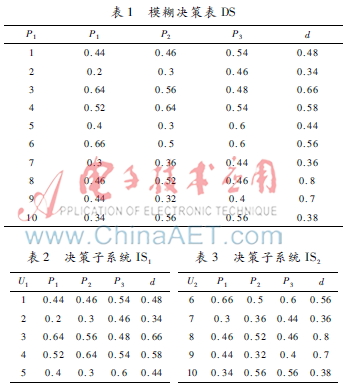
　　调用算法1，很容易得到F的模糊并行约简为P={P2,P3}，子表中对象对模糊正域的隶属度如表4所示。表4在子表IS1、IS2中对象对模糊正域的隶属度P1P2P3P1P2P1P3P2P3P1P2P3IS1H1(P)1.82.92.22.92.43.22.7IS2H2(P)1.53.42.83.52.83.83.5

　　模糊属性重要性矩阵T(A,F)与T(P,F)分别为：

　　DT1与DT2之间的概念漂移为：

　　FPRCDp2(DT2,DT1)=|0.20－0.20|=0

　　FPRCDp3(DT2,DT1)=|0.06－0.10|=0.04

　　FPRCDp(DT2,DT1)=1m∑mj=1|σ2,j－σ1,j|

　　=12(|0.20－0.20|+|0.06－0.10|)=0.02

　　因为条件属性P1对分类不起作用，是冗余的属性，删除之后，对分类起作用的属性P2、P3的概念漂移就彰显出来了。如果取δ=0.01，那么相对于单个属性P2、P3具有概念漂移，相对于整个并行约简P也具有概念漂移；如果取δ=0.05，那么相对于单个属性P2、P3及相对于并行约简P都不具有概念漂移。实际的数据流中，滑动窗口一般情况下是多个，可以类似地求出两个相邻窗口之间的基于模糊并行约简的概念漂移量。

3结论

　　传统的概念漂移探测方法不能探测模糊数据流中模糊概念漂移,并且其主要利用分类准确率的变化对概念漂移现象进行探测。本文提出了一种基于模糊并行约简的概念漂移探测方法。本文方法利用模糊数据的内部特性——模糊并行约简后的属性重要性的变化探测模糊概念漂移现象。

　　下一步的工作是研究模糊并行约简探测模糊概念漂移中δ的最佳取值，以及具体运用模糊并行约简构建分类器，与传统的概念漂移方法进行深入的分析比较。

参考文献

　　［1］ BABCOCK B, BABU S, DATER M,et al. Models and issues in data stream systems［C］. Proceedings of the 21st ACM SIGACTSIGMODSIGART Sympsium on Principles Database Systems, Madison, USA, 2002:16.

　　［2］ 王涛, 李舟军, 颜跃进, 等. 数据流挖掘分类技术综述［J］. 计算机研究与发展, 2007, 44(11):18091815.

　　［3］ 徐文华, 覃征, 常扬. 基于半监督学习的数据流集成分类算法［J］. 模式识别与人工智能, 2012, 25(2): 292299.

　　［4］ Jin Ruoming, AGRAWAL G. Efficient decision tree construction on streaming data［C］.Proceedings of the ACM SIGKDD the 9th International Conference on Knowledge Discovery and Data Mining, Washington, USA, 2003:571576.

　　［5］ 辛轶, 郭躬德, 陈黎飞,等. IKnnMDHecoc:一种解决概念漂移问题的方法［J］.计算机研究与发展, 2011, 48(4):592601.

　　［6］ 琚春华，帅朝谦，封毅，基于粒计算的商业数据流概念漂移特征选择［J］.南京大学学报(自然科学版)，2011，47(4):391397.

　　［7］ 邓大勇, 徐小玉, 黄厚宽. 基于并行约简的概念漂移探测［J］. 计算机研究与发展, 2015, 52(5):10711079

　　［8］ PAWLAK Z. Rough sets［J］. International journal of Information and Computer Science, 1982,11(5): 341356.

　　［9］ JENSEN R , Shen Qiang. Fuzzy–rough sets for descriptive dimensionality reduction［C］.Proceedings of 11th International Conference on Fuzzy Systems, Hawaii, 2002: 2934.

　　［10］ 李兴宽.集值信息下的粗集与知识获取［J］.微型机与应用,2015,34(23):1415.

　　［11］ 程昳,苗夺谦,冯琴荣.基于模糊粗糙集的粒度计算［J］. 计算机科学,2007,34(7):142149.

　　［12］ 徐菲菲,苗夺谦,魏莱,等.基于互信息的模糊粗糙集属性约简［J］. 电子与信息学报，2008,30(6):13721375.

　　［13］ 王国胤, 李德毅, 姚一豫，等.云模型与粒计算［M］.北京：科学出版社, 2012.

　　［14］ 陈林. 粗糙集中不同粒度层次下的模糊并行约简及决策［D］. 金华：浙江师范大学，2013.

　　［15］ 邓大勇, 徐小玉, 裴明华. F模糊粗糙集及其并行约简［J］. 浙江师范大学学报(自然科学版), 2015, 38(1):5866.

　　［16］ 邓大勇, 裴明华, 黄厚宽. F粗糙集方法对概念漂移的度量［J］. 浙江师范大学学报(自然科学版), 2013, 36(3):303308.

　　［17］ Yao Yiyu. Threeway decision with probabilistic rough sets［J］.Information Sciences, 2010, 180:341353.