钮浩东，黄洪琼

　　（上海海事大学 信息工程学院,上海 201306）

      摘要：针对船舶交通流预测中存在复杂性、非线性、受限因素多等特点，运用果蝇优化算法，建立了优化的广义回归神经网络船舶交通流预测模型。通过利用果蝇优化算法的全局寻优特性对广义回归神经网络进行参数优化，从而实现对船舶交通流的预测。以东海大桥的船舶流量观测数据为实例对象进行分析，通过MATLAB进行仿真预测，实验结果表明：FOA-GRNN模型相比于传统的GRNN模型和BPNN模型具有更高的预测精度和泛化能力，有效地解决了预测过程中数据样本少、非线性拟合能力差等问题，对水路的规划、通航管理等方面具有一定的应用价值。

　　关键词：船舶流量；果蝇算法；参数优化；预测；广义回归神经网络

0引言

　　随着经济的发展和国际贸易的不断增长，海上船舶数量显著增加，中国沿海地区和长江流域的船舶交通量也日益多元化。因此，精准地预测相关水域的船舶交通流量也日趋重要，其不仅能为航道的规划、设计、管理提供有力依据，还能提高通航效率，降低海上交通事故发生率。影响船舶交通流量预测的因素有很多，涉及政治、经济、人为等多方面的因素。目前国内外学者提出的预测方法有支持向量机［1］、组合预测［2］、回归分析［3］等，然而这些单一的预测方法难以满足在预测精度方面的预期要求。

　　为了克服传统预测方法存在的预测精度不高、非线性拟合能力不强、计算复杂等方面的不足，本文建立了一种新的船舶流量预测模型，即FO-GRNN模型，首次把果蝇算法（FOA）优化的广义回归神经网络（GRNN）运用到船舶交通流量预测中来。果蝇算法是根据果蝇寻找食物的活动演变而来的新兴算法，具有良好的全局寻优能力；另外广义回归神经网络的特点是具备优秀的局部逼近能力、较快的训练速度、处理非线性问题的优势明显。因此将两者有效地结合起来，通过利用FOA优化GRNN的相关参数来构建最优的预测模型，实现了预测船舶交通流量的目的。

1广义回归神经网络

　　斯坦福大学博士唐纳德·施佩希特于20世纪90年代初提出广义回归神经网络模型，其属于径向基(RBF)神经网络的一部分，相比于RBF网络，GRNN具有较强的局部逼近能力以及较快的学习速度［4］。另外，在样本数据较少的情况下，广义回归神经网络的预测结果也较优，其网络结构如图1所示。此网络由3个部分组成，分别为输入层、径向基层以及线性网络层。　　

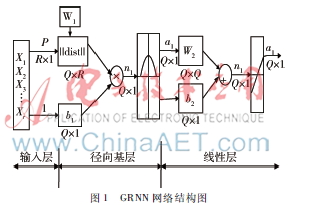
　　网络的第一层为信号输入层，输入向量经输入层传送至隐含层，其中隐含层包含Q个神经元，传递函数一般用高斯函数R=exp-x-c2σ2表示，式中σ称为平滑因子。输出层是一个特定的线性层，该层包含与隐含层数目相同的神经元，并且使用归一化点积权函数作为该层的权值函数，利用线性函数a2=purelin(n2)表示输出层的节点函数，从而计算出网络的输出值。

2FOA-GRNN预测模型的构建

　　果蝇优化算法是根据果蝇寻找食物的活动演变而来的一种全局寻优的新兴算法，在操作性、实用性和收敛速度等方面具有明显优势。

　　因为GRNN的性能受到σ取值的影响，所以本文使用果蝇算法来优化Spread值，主要思想就是通过果蝇嗅觉搜寻食物及视觉发现群体所在位置，从而使得Spread值取到最优解，然后使用迭代寻优的方法，将GRNN网络的预测值与真实值的均方差降至最低，记录这一时刻的味道浓度值，此值即为σ的最优解。图2为FOA-GRNN模型的流程图［5］，学习步骤如下。

　　（1）参数初始化，如果蝇的种群规模、迭代次数和初始位置。

　　（2）随机规定单个果蝇发现食物的所在位置和间隔距离。

　　（3）因为不清楚食物的具体位置，所以必须先求出所有果蝇相距原点的长度，然后求出味道浓度判定值S。

　　（4）建立味道浓度判定函数，把计算得到的S值代入到函数中，从而得到果蝇所在方位的味道浓度值。浓度判定函数选取GRNN模型里的均方差表示。

　　（5）求解果蝇群体中味道浓度的极值，即求均方差的极小值。

　　（6）记录最优味道浓度值和此时相应的果蝇位置。

　　（7）开始迭代寻优，循环执行步骤(2)~(5)，假如味道浓度优于前一代，则进行步骤(6)。

　　（8）判断迭代次数条件是否满足，若满足则得到Spread最优解，并将其带入最优的GRNN模型进行仿真预测，否则返回步骤(2)继续执行。

3实例仿真与分析

　　3.1实验数据及参数设置

　　以上海洋山港东海大桥观测面经过的船舶为研究对象，根据上海洋山港统计的数据，选取2015年4月15日至2015年7月5日的船舶流量数据作为预测的原始数据。前50天数据作为训练数据，后32天数据作为测试数据。选取上海GDP指数、运输成本、业务量指数、船舶平均吨位、天气情况5个指标作为主要影响因素来建立预测模型。为了减小预测误差，实现多类别样本的统一分析，确保数据保持在同一数量上，故在实验前先对数据进行归一化处理，公式如下所示［6］：

　　仿真试验时，选取MATLAB神经网络工具箱中的newgrnn函数来得到Spread最优值，构建最佳的FOA-GRNN船舶流量预测模型。通过反复验算设定FOA的参数如下：初始化果蝇群体位置区间为［0,100］，果蝇群体规模为30，迭代次数为200。经过FOA优化后，得到最优的Spread值为0.002 2。

　　3.2仿真结果对比分析

　　为了对实验结果进行对比分析，本文分别计算了3种算法的MAD、MAPE、RMS。设xt为实际流量值，t为预测值，n为预测序列总数，其相应公式依次为［7］：

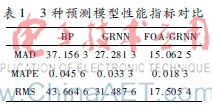
　　将这3种预测模型进行性能指标对照，其比较结果如表1所示。此外，为了凸显本文优化方法的优越性，分别对BP神经网络模型、GRNN模型和FOAGRNN模型进行表13种预测模型性能指标对比BPGRNNFOAGRNNMAD37.156 327.281 315.062 5MAPE0.045 60.033 30.018 3RMS43.664 631.487 617.505 4仿真实验及比较，仿真结果如图3~图5所示。

　　由图3~图5及表1可知，虽然BP网络模型和单一的GRNN网络模型都得到了相应的预测结果，但是在预测精度上还是不及FOAGRNN模型。由于BP神经网络需要大量的训练样本，有时样本数条件无法达到要求，此外由于神经网络中的过拟合现象和GRNN中Spread值的选择问题，使得这两种算法的预测精度没有达到预期的要求。FOA具有较强的全局寻优能力，利用FOA优化GRNN模型的Spread值，得到其最优解，使得预测误差达到最小。

　　由表1可知，应用FOAGRNN模型预测的MAD、MAPE、RMS值都比单一的GRNN模型和BP模型小，由此说明，相对于BP和GRNN网络，FOAGRNN网络模型的预测误差较小并且具有较高的稳定性，FOAGRNN模型在预测能力、逼近能力等方面皆具有较强的优势。

4结论

　　本文首次将果蝇算法优化的广义回归神经网络模型应用于船舶交通流量预测中，根据FOA算法的全局寻优特性对GRNN网络中的Spread值进行优化，充分考虑多方面因素的影响，构建了FOAGRNN船舶交通流量预测模型，其具有如下特点：

　　（1）良好的拟合能力和泛化能力。通过MATLAB仿真实验证明此模型具有良好的预测能力，与BP和GRNN模型相比，该模型的绝对值平均误差、相对误差绝对值平均值、均方根误差都比较小，具备更优的预测精度。

　　（2）良好的稳定性和快速收敛能力。该模型需要确定的参数少，能够很好地避免人为主观臆断的影响。

　　综合分析，FOAGRNN模型的实现过程简单，泛化能力强，预测精度较高，为船舶交通流量预测提供了一种新途径。

参考文献

　　［1］ 冯宏祥，肖英杰.基于支持向量机的船舶交通流量预测模型［J］.中国航海，2011,34(4)：6266.

　　［2］ 吕靖，方祥麟.船舶交通量的组合预测模型与方法［J］.大连海事大学学报，1996，22(2)： 3335.

　　［3］ 张杏谷.回归分析方法在VTS预测研究中的应用［J］.中国航海，1996(2)：3235.

　　［4］ 刘敬贤，刘振东.基于广义回归神经网络的船舶交通量预测模型［J］.中国航海，2011，34(2)：7478.

　　［5］ 聂娜娜.修正型果蝇算法优化GRNN网络的尾矿库安全预测［J］.计算机工程，2015，41(4)： 267272.

　　［6］ 沈浩,黄洪琼.基于PSO优化SVM的船舶流量预测算法［J］.微型机与应用,2015,34(5):7375.

　　［7］ 郎茂祥.预测理论与方法［M］.北京：清华大学出版社，北京交通大学出版社，2011.