PSODE混合算法的ADRC控制-AET-电子技术应用

PSODE混合算法的ADRC控制

2016年电子技术应用第6期

王子豪，杨小健

南京工业大学计算机科学与技术学院，江苏南京211816

摘要： 针对自抗扰控制过程中存在的最优参数难以确定的问题，提出一种基于混合PSODE的参数调整算法。采用线性ADRC控制器，利用ITAE值作为子项对系统动态性能进行评价，对于振幅回撤较大的输出增加惩罚策略；针对ADRC控制参数较多、难优化的问题，采用混合PSODE算法进行优化：当PSO的搜索停滞时，新算法异步间歇对pbest空间进行变异，并自适应调整惯性权重使粒子收敛，平衡了算法的全局和局部搜索能力。最后利用所提出的控制算法对锅炉过热汽温系统控制模型进行仿真，结果显示优化后的控制系统具有良好的控制性能和鲁棒性。

关键词： ADRC 参数优化变异 DE PSO

中图分类号： TP18
文献标识码： A
DOI：10.16157/j.issn.0258-7998.2016.06.025
中文引用格式： 王子豪，杨小健. PSODE混合算法的ADRC控制[J].电子技术应用，2016，42(6)：91-93，97.
英文引用格式： Wang Zihao，Yang Xiaojian. ADRC control based on PSODE hybrid algorithm[J].Application of Electronic Technique，2016，42(6)：91-93，97.

ADRC control based on PSODE hybrid algorithm

Wang Zihao，Yang Xiaojian

School of Computer Science and Technology，University of Nanjing Technology University，Nanjing 211816，China

Abstract： According to the problem that the optimal parameters are difficult to be determined in the process of active disturbance rejection controller, a hybrid PSODE algorithm is proposed. It sets up the process of linear ADRC parameter optimization controller, uses the ITAE value the system dynamic performance evaluation as a child, and adds the punishment strategy for larger amplitude retracement output. For solving the problem of how to optimize ADRC control parameters, mixing PSODE algorithm is raised: When PSO′s search is stagnant, asynchronously and intermittently, the pbest space will be mutant under new algorithm, and the small inertia weight particle converges, which balances the global and local search ability of the algorithm. Finally the proposed control algorithm is used to control the boiler superheated steam temperature system simulation model. The results show that the optimized control system has good control performance and robustness.

Key words : ADRC；parameters optimization；mutation；DE；PSO

0 引言

自抗扰控制器（Active disturbance rejection controller）是一种非线性控制器^[1]，该控制器将系统模型的内部扰动和外部扰动看为总扰动，通过扩张观测器对总扰动进行估计和补偿。因此，ADRC可以有效解决一些非线性不确定系统的控制问题^[2-3]。相对于非线性自抗扰控制器，线性自抗扰控制器设计简单，控制器参数调节有相对确定的方法^[4]。ADRC是否能充分发挥其性能依赖于控制器的参数设置是否最优。ADRC需要优化的参数较多，若依靠经验调试线性ADRC的参数，非常耗时，且无法保证系统响应最优或次优。文献[5]采用各种算法对线性自抗扰控制器多参数整定问题进行调优。但这些方法复杂，实际应用有一定难度。

PSO算法在算法早期迭代时的效果很好，但在邻近最优解时出现了停滞。DE算法的多样性及搜索能力的鲁棒性较强，但后期收敛速度较慢。针对这个问题，本文提出一种PSODE混合优化计算方法。新算法的前期基于惯性权重改进策略有效扩大搜索步长，粒子大范围搜索。当PSO的搜索停滞时，对pbest空间进行变异同时自适应调整粒子搜索步长，既避免了算法出现早熟问题增加粒子的多样性，又利于粒子加速收敛，保证寻优速度。本文采用该算法应用于优化线性自抗扰控制器的参数，并进行了仿真研究，结果表明可以有效提高系统的控制性能。

1 线性ADRC控制器

二阶线性ADRC控制器的结构图如图1所示。图中y和r是控制器输出和参考输入信号。u为控制量，d为未知外扰，Gp是被控对象。ESO（Extended State Observer）为扩张状态观测器。

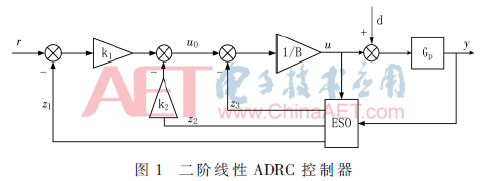
二阶线性ADRC中ESO的一般形式：

2 PSODE混合算法

2.1 标准PSO算法

粒子群优化算法是一种收敛速度快、算法简单的全局优化进化算法。pbest和gbest分别表示粒子的最优位置和群体的最优位置，可以把它们看成PSO算法的两个输入。PSO算法中，随着迭代次数增加，粒子的多样性会逐渐减小，这增加了陷入局部最优的可能性。

2.2 标准DE算法

DE算法首先在搜索范围内随机生成粒子，再采用变异、交叉、选择三大步骤来更新种群，其更新过程与遗传算法类似。

因为DE含有变异属性和交叉属性，所以相比PSO，DE算法全局搜索性能更好一些。但是，这种变异性可能带来收敛速度慢的问题，导致局部搜索性能降低。

2.3 惯性权重改进策略

权重系数的取值研究是改进PSO算法的重点。根据粒子与当前种群最优值的平均距离和粒子与当前种群的最大距离对惯性权重进行改进。

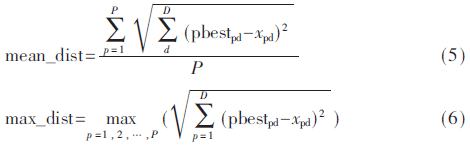
距离变化率的定义为:

k的取值随着粒子与当前种群最优值的平均距离和粒子与当前种群的最大距离变小而变小，表明需要提高它的精细搜索能力，反之，则需要提高它的全局搜索能力。η的取值：

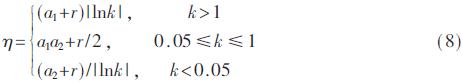
其中，a₁=0.3，a₂=0.2，r为[0，1]间均匀分布的随机数，η的值随迭代次数的变化而变化，可以提高前期粒子搜索范围和粒子后期的搜索精度。

2.4 PSODE混合策略

本文提出了PSODE混合算法，DE算法中的变异性可以为粒子提供更好的多样性，本文为pbest和gbest两项提供变异差分性能，确保全局搜索能力。混合策略有两个条件：(1)当PSO算法中L百分比的种群出现停滞现象。(2)如果这些点连续停滞S次，若满足条件则异步间歇性调用R次DE算法，混合策略如图2所示。

根据以上分析，PSODE算法步骤如下：

步骤(1)：初始化种群，输入算法各参数。

步骤(2)：计算粒子适应度，得到初始个体极值x^pbest(k)，p=1，…，P和全体极值x^gbest(k)。

步骤(3)：对粒子群位置和速度进行更新，计算适应度，更新个体极值x^pbest(k)，p=1，…，P和全体极值x^gbest(k)。

步骤(4)：检查混合调用条件，如果L个pbest的搜索点保持不变，且连续停滞S次，那么异步间歇性调用R次混合算法。若满足调用条件，跳到步骤(5)，否则进行步骤(8)。

步骤(5)：在个体极值x^pbest(k)，p=1，…，P中随机取3个互不相同的粒子r₁、r₂、r₃，对其采取变异策略得到y^L(k)。

步骤(6)：对变异后的粒子进行交叉。

步骤(7)：选取较小适应度值的位置作为pbest，并更新gbest的位置。DE调用次数小于R时回到步骤(5)，否则进行步骤(8)。

步骤(8)：若满足结束条件，输出gbest，算法终止，否则返回步骤(3)。

3 基于PSODE算法的ADRC控制器设计

3.1 适应度函数的选择

本文选用ITAE值作为一个子项来评价系统的动态性能，将上升时间t_r、超调量σ、控制能量u以不同的形式综合到评价函数中。系统输出信号达到目标值后不仅会有超调，也有可能产生信号回撤，为了防止系统信号回撤较大，加入惩罚因子λ₅。性能评价函数如式(9)所示。

3.2 PSODE混合算法流程

适应度函数被确定后，对控制器的参数进行寻优。在满足约束条件的前提下，适应度函数的数值达到最小时所对应的参数为最优参数。PSODE算法优化线性ADRC控制器问题的优化设计流程图如图3所示。

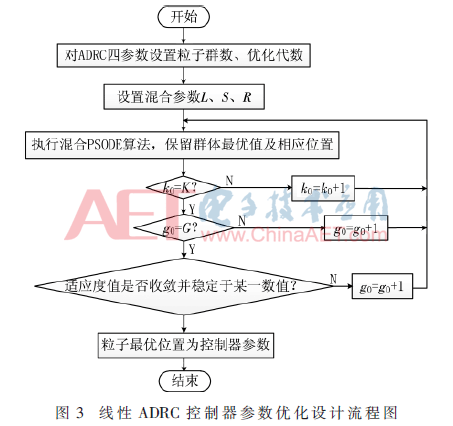
4 锅炉过热气温系统的仿真实验

以文献[7]负载为75%工况为例，采用串级控制系统对其进行设计。图4为串级控制系统的结构框图。

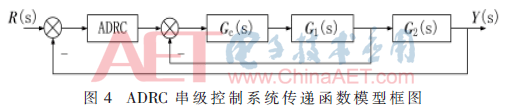
副回路比例值为100。首先用交叉两点法对被控回路进行降阶，得到一阶滞后近似模型：

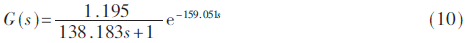
根据文献[8]，设计H无穷非脆弱鲁棒PID控制器，得到PID控制器参数为：K_P=0.908，K_I=0.004 3，K_D=45。

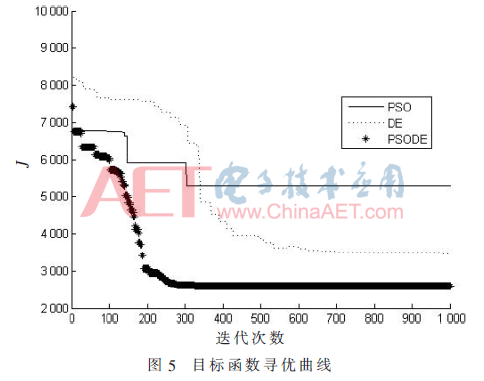
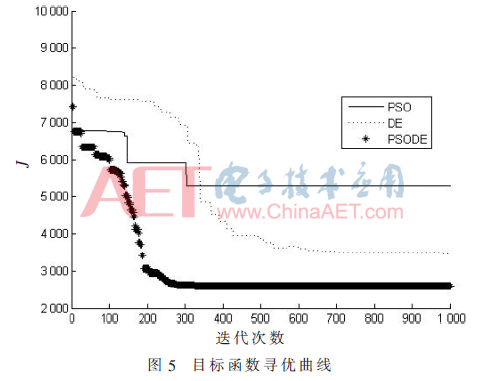
B取被控对象传递函数分子部分的零阶系数为1.195。根据文献[9]将PID参数转化为ADRC参数，得到需要整定的4个参数的初始值，通过本文提出的PSODE算法与DE和PSO算法分别对这4个参数的取值进行寻优。目标函数J的优化过程曲线如图5所示。从图中可以看出随着迭代次数的增加，PSODE较其他两种算法有更快的收敛速度，且没有陷入局部最优，最终收敛找到了最优解。

4.1 阶跃响应仿真

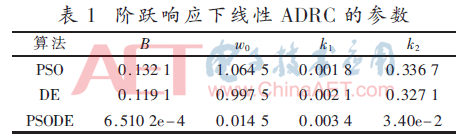
经过3种算法优化后的ADRC参数如表1所示。给不同参数下的控制系统输入阶跃信号，其系统输出信号如图6所示。

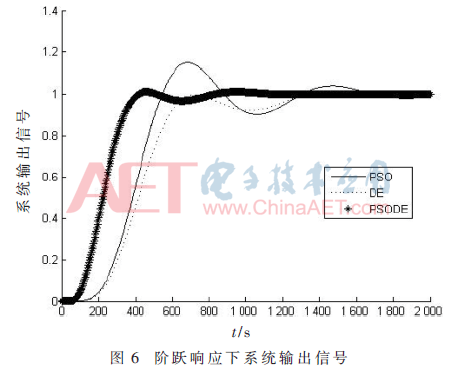
由图6可以看出，基于PSODE优化的线性ADRC系统反应速度最快，几乎没有超调，控制效果最更好。

4.2 鲁棒稳定性分析

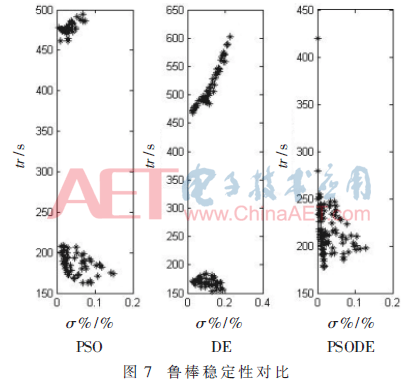
采用Monte-Carlo随机试验方法评价控制系统性能鲁棒性。令控制器参数发生±10%的随机变化，计算tr、σ%性能指标，重复仿真100次。

图7中动态分布点是一个二维向量的集合，点越集中说明性能鲁棒性越好。由图7可以看出，PSODE下的点分布较为集中且超调较少，基于PSODE优化的控制系统比另外两种系统具有更强的鲁棒性。

5 结论

针对自抗扰控制过程中存在的最优参数难以确定的问题，在对PSODE混合算法和自抗扰控制理论深入研究的基础上，提出了基于PSODE 算法的自抗扰控制器优化设计。提出的带惩罚策略的评价函数在混合PSODE算法的框架下，可以更快地计算出控制器参数，寻优精度、收敛效果和稳定性等方面相对于传统的算法均得到了很大的提高。同时也验证了本文提出的算法加强了控制系统的鲁棒性，提高了控制系统的控制能力。

参考文献

[1] 韩京清.从PID技术到“自抗扰控制”技术[J].控制工程，2002(3)：13-18.

[2] LI D，LI C，GAO Z，et al.On active disturbance rejection in temperature regulation of the proton exchange membrane fuel cells[J].Journal of Power Sources，2015，283：452-463.

[3] TANG H，LI Y.Development and active disturbance rejection control of a compliant micro-/nanopositioning piezostage with dual mode[J].IEEE Transactions on Industrial Electronics，2014，61(3)：1475-1492.

[4] GAO Z.Scaling and parameterization based controller tuning[C].Proc.of the 2003 American Control Conference，2003：4989-4996.

[5] ZHANG Y，FAN C，ZHAO F，et al.Parameter tuning of ADRC and its application based on CCCSA[J].Nonlinear Dynamics，2014，76(2)：1185-1194.

[6] LI D，GAO Z，CHEN X，et al.Tuning method for second-order active disturbance rejection control[C].中国自动化学会控制理论专业委员会D卷，2011：6322-6327.

[7] Xia Yuanqing，Liu Bo，Fu Mengyin.Active disturbance rejection control for power plant with a single loop[J].Asian Journal of Control，2012，14(1)：239-250.

[8] 恒庆海，鲁婧，恒庆珠，等.纸张定量系统H∞非脆弱鲁棒控制器设计[C].第二十九届中国控制会议论文集，2010.

[9] ZHAO C，LI D.Control design for the SISO system with the unknown order and the unknown relative degree[J].Isa Transactions，2013，53(4)：858-872.

原创声明：此内容为AET网站原创，未经授权禁止转载。

相关内容