刘清华，杨桂芹，张妍妮

　　（兰州交通大学 电子与信息工程学院，甘肃 兰州 730070）

　　摘要：随着数据采集能力和采样频率的不断提高，采用传统的奈奎斯特采样定理会获得海量的数据，这给信号的存储和传递带来了极大挑战。提出基于稀疏快速傅里叶变换的信号压缩方法，利用信号在频域的稀疏性，压缩信号所需的存储空间，在保证拥有足够小的误码率的前提下，以高概率重构原始信号。

　　关键词：稀疏快速傅里叶变换；信号压缩；重构

0引言

　　传统的信号离散化基本依据——奈奎斯特采样定理认为，在进行模拟/数字信号的转换过程中，当采样频率大于信号中最高频率的2倍时，采样之后的数字信号完整地保留了原始信号中的信息，而实际应用中一般需要5～10倍才能达到理想的效果。然而，近十几年传感系统获取数据的能力不断增强，采样频率越来越高，需要处理的数据量也不断增多，这就给信号处理的能力提出了更高的要求。

　　2012年，麻省理工学院（Massachusetts Institute of Technology, MIT）的4位研究员提出了一种新的信号处理算法——稀疏快速傅里叶变换（Sparse Fast Fourier Transform，SFFT）［12］。它通过利用信号频域的稀疏特性，以与信号长度成亚线性关系的时间复杂度及高概率重构出信号完整频谱，其效率是传统快速傅里叶变换（Fast Fourier Transform, FFT）算法的10～100倍。

1稀疏快速傅里叶变换理论

　　离散傅里叶变换（Discrete Fourier Transform, DFT）作为一种重要的变换手段被广泛应用于信号处理、通信、音频/图片/视频的压缩等领域。FFT作为实现DFT变换最快速的方法而被广泛使用，对n维信号的FFT时间复杂度为O(nlogn)。

　　但在实际应用中，大部分的傅里叶系数很小或者等于0，只有少部分的系数是不可忽略的，而这少部分系数正是信号恢复中必不可少频率值。如果对信号不假思索地使用FFT处理，那么就会花费大量的运算时间在并不关心的零频点上。

　　对n维离散信号，参考文献［2］中指出：

　　（1）若信号为精确k稀疏信号，则SFFT的时间复杂度为O(klogn)；

　　（2）若信号为一般信号，则SFFT的时间复杂度为O(klognlog(n/k))。

　　对于任意k∈Rn，两种情况都比FFT要快。

　　1.1SFFT理论框架

　　图1SFFT理论框图SFFT是利用信号频谱的稀疏性来降低DFT运算的复杂度的算法，其理论框图如图1所示。SFFT算法是将数量为n的信号频率系数按规律H投入B个“筐”中。因为信号在频域是稀疏的，所以每个框中很高的概率只会分得一个大系数。如此便将长度为n的信号转换成了长度为B的信号了，且Bn。对变换后的信号做B点FFT。最后设计重构算法H－1恢复出大频率系数的位置和幅值，从而得到原始信号的频谱。

　　1.2SFFT相关数学符号

　　设信号x∈Cn，其中n为信号的长度且n=2a（a为正整数），信号x的傅里叶频谱为。k表示信号稀疏度。x*y表示x与y的卷积，x·y表示x与y的乘积，即有x·y=*。supp(x)表示x的一个支撑集，即x非零坐标的集合。本文定义ω=e2πi/n。

　　1.3频谱重排

　　参考文献［3］中指出，信号在时域的二次采样会引起频域的频谱混叠。因此，可以通过时域的二次采样达到频谱重排的效果，从而降低频谱长度。设传递函数为Pσ,τ，其中σ为奇数且对n的取模运算可逆，整数τ∈［n］。可得

　　故，换元得到时域重排后引起频域变化的公式为：

　　参考文献［1］指出，如果j≠0，n为2的整数次幂，且σ∈［n］是一个均匀随机奇数时，则大傅里叶系数落在同一个“筐”中的概率为：

　　P{σj∈［－C,C］}≤4C/n

　　如果n不是2的整数次幂，就在信号后边添加若干个0，使其长度为2的整数次幂。

　　1.4平滑滤波器

　　数字信号处理领域拥有多种类型的滤波器，滤波器可以将感兴趣的部分从原始信号中分离出来，进而进行特殊处理。在SFFT算法中需要一个时域和频域的能量都集中且其通带和阻带纹波较小的滤波器。满足上述要求的首推理想低通滤波器，但在实际中理想低通滤器无法实现，通常通过截断并卷积其他窗函数而实现。时域的Sinc(·)函数其频域为矩形窗函数，截断后由于其时域的不连续性导致截断后的频域响应在通带和阻带出现了明显的纹波。参考文献［4］指出，凯泽窗和道尔夫切比雪夫窗可以控制通带和阻带的纹波。因此，本文的平滑滤波器采用截断后的Sinc(·)与道尔夫切比雪夫窗卷积的方式实现。以下给出具体实现过程。

　　定义：设F(ε,δ,w)∈Rn为定义域内的一组对称序列，若F满足：

　　则称F为标准窗函数。

　　参考文献［1］指出，对于任意给定阻带截断因子ε和震荡纹波δ，总可以构造出一个标准窗函数:

　　但是，这个标准窗函数只规定了阻带特性，在通带内仍然有较大的纹波，影响算法效率。

　　定义：设F(ε,ε′,δ,w)∈Rn为定义域内的一组对称序列，若F满足:

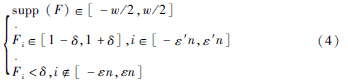
　　则称F为平滑窗函数，其中ε′为通带截断因子，其他符号与公式（3）相同。

　　本文采用道尔夫切比雪夫窗与矩形窗函数卷积生成平滑滤波器，用符号G表示。当然用凯泽窗代替道尔夫切比雪夫窗也可以实现平滑滤波器，这里不再赘述。

　　将时域重排的信号通过平滑滤波器，生成函数y=G·(Pσ,τx)，所以：

　　yi=Gixσi+τ，supp(y)supp(G)=［w］（5）

　　由平滑滤波器的设计过程可知，只需要确定信号长度n和稀疏度k便可构造出平滑滤波器，这与信号具体内容无关。所以滤波器的设计可以在算法执行前的预处理阶段完成，这样不仅降低了算法的运算量，同时不必将滤波器数据传输到接收端，提高了数据压缩比。

　　1.5频域降采样

　　由公式（5）知信号y∈Cw，设“筐”的数量为B，且B整除信号长度w。现令：

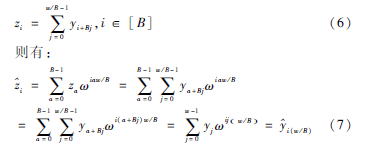
　　可见，时域的混叠造成了频域的等间隔采样，即频域降采样［5］。

　　1.6重构算法

　　重构过程主要分为3步：哈希映射、定位循环和估值循环。

　　设哈希映射函数为hσ(i)=round(σiB/n)，它确定了分“筐”的规则。同时设偏移量向量oσ(i)=σi－hσ(i)(n/B)，它确定了估值循环时滤波器的坐标。定位循环得到i中最大的前dk个值的坐标J，经过哈希函数反映射得到J的原像I={i∈［n］|hσ(i)∈J}。对于i∈I，由′i=hσ(i)ωτi/oσ(i)得到原始信号x的逼近值。

　　因为平滑滤波器通带几乎平滑，阻带以指数衰减，所以相邻大值点之间的频谱泄露可以忽略。因此，重构算法不需要迭代，结构简单［6］。此外，为协调“分筐”的开销和重构估值的开销，取参数B≈n·k，且B整除n。

　　2SFFT算法信号压缩的仿真与评价

　　为验证算法的可行性，本文构建了多个不同参数的一维稀疏信号，在长度为n的信号中，均匀随机选取k个位置为非零值，其余设置为零值。在算法耐噪声测试中，采用高斯白噪声作为信号传递过程中的信道噪声。

　　图2是其中一个测试用例的原始信号和恢复信号对比图，其信号长度为65 536，频域稀疏度为50，信道信噪比为20 dB。从图中可以看出即使较小的频点幅值依然可以高概率重构出来。

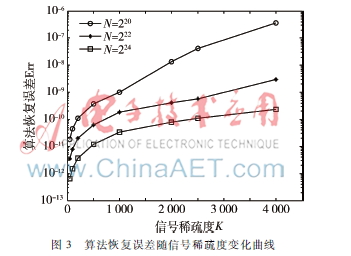
　　图3是描述算法重构误差随信号稀疏度的变化曲线。选取测试用例中信号长度分别为220、222、224、稀疏度在50～4 000之间变化的测试信号。由图3可知当信号长度一定时，SFFT算法的恢复误差随稀疏度的增大而逐渐增大；当信号的稀疏度一定时，信号长度越长SFFT算法的恢复误差越小。总之，信号的大系数在信号中占的比例越大，其恢复误差就越大；在大系数个数比较少的情况下，其算法的恢复误差可以低于1×10-10。

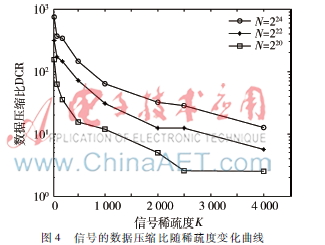
　　图4是不同稀疏度的情况下SFFT算法的数据压缩比变化曲线。横向比较可以看出，在信号长度一定的情况下，其非零点越多，在信道传输存储所需的物理单元就越多，则其数据压缩比就越小。当信号长度为224、信号稀疏度为50的时候，SFFT的数据压缩比高达741.436；当信号长度为224、信号稀疏度为4 000的时候，SFFT的数据压缩比降到了12.722。纵向比较可以看出，当信号稀疏度一定的情况下，信号长度越长其压缩比越大。

3结论

　　本文通过通过分析传统信号压缩的不足，提出一种基于稀疏快速傅里叶的信号压缩方式。该方法通过利用信号频域的稀疏特性，成功降低了信号进行傅里叶变换的长度，在保证足够小的误码率的情况下，使传输信号具有良好的数据压缩比，同时使计算傅里叶变换的时间大大缩短。通过构建参数不同的信号进行SFFT算法仿真，证明该算法在信号压缩方面拥有很大的优势。

参考文献

　　［1］ HASSANIEH H, INDYK P, KATABI D, et al. Simple and practical algorithm for sparse Fourier transform［C］. Proceedings of the TwentyThird Annual ACMSIAM Symposium on Discrete Algorithms， SIAM, 2012: 11831194.

　　［2］ HASSANIEH H, INDYK P, KATABI D, et al. Nearly optimal sparse Fourier transform［J］. Association for Computing Machinery, 2012:563578.

　　［3］ GILBERT A C, MUTHUKRISHNAN S, STRAUSS M. Improved time bounds for nearoptimal sparse Fourier representations［J］. Proceedings of SPIE, 2005, 5914:398412.

　　［4］ DINIZ P S R， da SILVA E A B， NETTO S L. 数字信号处理系统分析与设计(原书第2版)［M］. 张太镒，汪烈军，于迎霞，译.北京: 机械工业出版社, 2013.

　　［5］ HSIEH S H, LU C S, PEI S C. Sparse fast Fourier transform by downsampling［C］. 2013 IEEE International Conference on Acoustics, Speech, and Signal Processing, 2013:56375641.

　　［6］ 那美丽, 周志刚, 李霈霈. 基于稀疏傅里叶变换的低采样率宽带频谱感知［J］. 电子技术应用, 2015, 41(11): 8588.