陈超辉，文志强 ，胡俊飞

　　(1. 湖南工业大学 计算机与通信学院, 湖南 株洲 412007；2.智能信息感知及处理技术湖南省重点实验室, 湖南 株洲 412007)

       摘要：误差扩散算法最早是由FloydSteinberg提出，并在当时成为处理效果最好的算法之一。它可以输出视觉效果良好的半色调图像，因而得到了广泛的推广。为改善该传统误差扩散算法均易在中频区域产生结构性纹理现象，提出了一种基于跳跃扫描路径的误差扩散半色调算法。算法在对像素点进行扫描时会根据一定的条件进行跳跃扫描，直接处理若干像素点之后的像素，并将处理后的误差扩散至相邻但还未经处理的像素点上。大量的实验表明，合理的跳跃距离能够帮助有效地抑制半色调图像中的结构性纹理，得到效果更好的半色调图像，具有更深远的意义和实际应用价值。

　　关键词：跳跃扫描；误差扩散；中频区域；结构性纹理

0引言

　　数字图像半色调技术是基于人眼视觉系统低通滤波特性和图形成像原理，利用数学、计算机及其他工具在二值或多值设备中模拟原灰度图像再现的一门技术。它适用于所有工作原理为有限值记录的设备，是数字印刷过程中的关键技术之一。研究表明，人眼视觉系统具有低通滤波特性，在相隔一定距离观察物体时，会将物体在空间上较为接近的部分视为整体。通过这一特性，当人眼观察半色调结果图像时，会从整体上形成连续色调的效果，但是传统误差扩散半色调算法得到的半色调图像中存在明显的结构性纹理和“蠕虫”现象。

　　误差扩散半色调算法应用范围一直与人们的生活息息相关。1975年FLOYD R W和STEINBERG L首次提出了误差扩散算法［1］，将误差按照一定的权值扩散至邻近的未经处理的像素点上，实现了从单独的点处理到单点及邻域处理的转变，算法复杂度低，输出的半色调图像效果好。但是在半色调图像中仍然存在一定的不合理现象：输入图像中频区域在对应的半色调图像区域中存在较多的结构性纹理，在光亮和光暗部分容易出现波浪线即“蠕虫”现象［2］。为解决这两个问题，后来的研究人员对该传统误差扩散算法进行了诸多的改进。在ULICHNEY R A发现误差扩散算法产生的半色调图像视觉效果与半色调图像中隐藏的蓝噪声特性有关之后，许多研究者依据蓝噪声特性一步改善了误差扩散半色调算法［3］。VELHO L等人提出空间填充曲线的方法［4］，该方法虽然实验效果较好，但算法复杂度高。

　　OSTROMOUKHOV V提出了在不同的灰度级上采用不同误差扩散系数［5］，参考文献［6］中通过改进误差扩散滤波器系数来改善实验效果［6］。受国际研究热潮的影响，国内逐渐从背景原理［7］入手，同时也跟紧潮流提出了各种改进的半色调算法［89］。近些年我国台湾国立科技大学郭景明教授及其团队一直致力于图像半色调技术的研究，提出了多种半色调技术方法如：蓝噪声特性与误差扩散滤波器结合［10］、多灰度级整体替换［11］、点扩散方法和误差扩散模型结合等，这些新方法都不同程度上提高了半色调图像的质量。本文采用了一种通用的图像质量评价方法对半色调图像质量进行评价［12］。

　　虽然这些方法在一定程度上提高了半色调图像的质量，但是始终没有摆脱半色调结果图像中存在较多的非期望性纹理的问题，尤其是在某些特定的灰度级上存在较为明显的结构性纹理，高光、暗调区域存在明显的波浪线。针对以上这些算法中存在的明显问题及误差扩散中算法中几个关键因素（像素点扫描方式、误差扩散滤波器模型、自适用阈值），提出了一种基于跳跃扫描路径的误差扩散半色调算法。该算法主要通过改变影响半色调图像效果的扫描路径，采用自适用阈值的方式来达到更好的实验效果，该实验过程中既采用传统误差扩散滤波器的模型又采用了新设计的误差扩散滤波器模型。为了从客观上评价各个实验得到的半色调图像质量，采用通用图像质量评价指标峰值信噪比(Peak Signal to Noise Ratio, PSNR)来进行判断。

1传统误差扩散算法

　　误差扩散算法由于算法复杂度低，实验效果良好，因此一直是应用最广泛的算法之一。传统误差扩散算法的核心思想是将灰度图像当前像素点像素值与某一设定的阈值T相比较，若当前像素点像素值大于T，则将当前像素点像素值赋为255，并将误差按照一定的方式扩散到周边未经处理的像素点上；反之则将当前像素点的像素值赋0，同样将误差扩散到未经处理的像素点上。现假设P(m, n)为图像像素点的原像素值，I(m, n)为误差扩散后图像像素点的像素值，Q［ ］为量化阈值，B(m, n)为输出图像的像素值，E(m, n)为点(m, n)处产生的误差值，W(m, n)为误差扩散滤波器的系数，T(m, n)为像素点(m, n)处对应的阈值，在改进的算法中将采用自适应方法获取每个像素点对应的阈值。

　　(1)用公式表示原理如下：

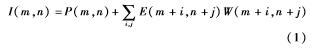
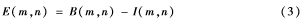
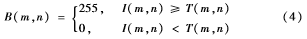
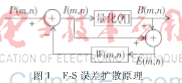
　　(2)原理框图如图1、图2所示。

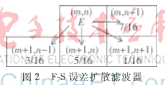
2跳跃扫描误差扩散算法

　　相对传统误差扩散算法，本文提出的跳跃扫描误差扩散数字半色调算法做了四点改变：(1)改变了扫描的方式，以跳跃扫描方式替代原来的光栅、蛇形扫描。(2)改变了阈值的计算方式，采用了自适应阈值方法。(3)改变了误差扩散的具体方式。

　　2.1扫描方式

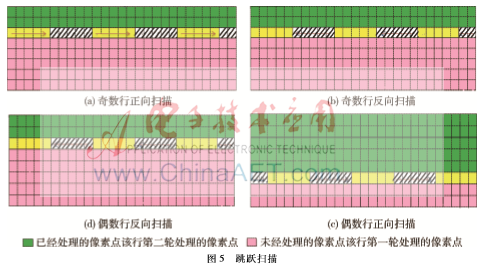
　　研究表明半色调图像质量与像素点扫描方式有关，目前像素点扫描方式有光栅扫描、蛇形扫描［2］、空间填充曲线［4］，能在一定程度上改善半色调图像质量，但是在某些特定灰度级上始终存在结构性文理。由图3、4可知不论是光栅还是蛇形扫描方式，在处理同一行上的像素点时，误差均只能朝一个方向扩散，这容易使得半调图像中行与行之间产生纹理。本文提出一种跳跃扫描方式，使得同一行上产生的误差同时朝左右两个方向扩散，同时该方式也是一种蛇形扫描方式，能更有效降低半调图像中纹理。其基本思想是：同一行分左右两个处理过程，如图5所示。

　　2.2基于自适应的误差扩散方式

　　(1)自适用阈值计算

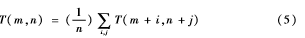
　　式中N要根据当前像素点的位置确定，表示当前像素点周围像素点的总个数。

　　(2)误差扩散方式（从左至右扫描）

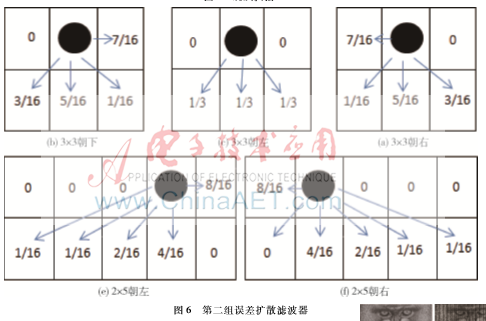
由于参考文献［6］的误差扩散系数能够有效地去除输入图像在光亮和灰暗区域的线条，因此在高灰度和低灰度区域采用该误差扩散滤波器。奇数行从左向右扫描，中频区采用图6(a)滤波器，非中频区采用图6(e)滤波器；奇数行从右向左扫描，若左边的像素点已被处理，则中频区和非中频区均采用图6(b)滤波器，若左边的像素点没被处理，则中频区采用图6(c)滤波器，非中频区采用图6(f)滤波器。偶数行从右向左扫描，中频区采用图6(c)滤波器，非中频区采用6(f)滤波器。偶数行从左向右扫描，若右边的像素点已被处理，则中频区和非中频区均采用图6(b)滤波器，若右边的像素点没被处理，则中频区采用图6(a)滤波器，非中频区采用图6(e)滤波器。

3实验结果分析

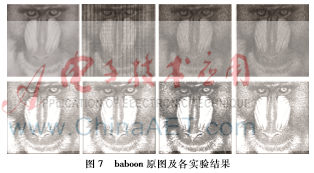
　　文中提到了多种误差扩散算法，着重分析了三种传统算法的原理和实现过程，并分析了各个算法的优缺点。最后提出了基于跳跃扫描路径的误差扩散算法。为了验证该算法的优越性，选择了大量的灰度图像进行测试。实验结果如图7，8，9所示，评价指标为PSNR，结果如表1，2，3所示。

　　表1是对图7用各种算法计算出来的PSNR。 表2是对图8用各种算法计算出来的PSNR。表3是对图9用各种算法计算出来的PSNR。从表中可以得知各算法的优略，其中JS(N)表示跳跃扫描算法，N表示跳跃距离（以像素为单位）。

4结论

　　通过实验分析、对比表明，跳跃扫描误差扩散半色调算法和传统误差扩散半色调算法复杂度相当。就实验效果而言，在一定跳跃距离范围内跳跃扫描误差扩散算法优于蛇形扫描误差扩散算法，而蛇形扫描误差扩散算法优于光栅扫描误差扩散算法。就跳跃扫描算法本身的各组实验而言，d=5为最佳的跳跃距离。

　　参考文献

　　［1］ FLOYD R W, STEINBERG L. An adaptive algorithm for spatial greyscale［C］. Proceedings of International Symposium of SID， 1976: 36 37.

　　［2］ ULICHNEY R A. Digital halftoning［M］. Cambridge: MIT Press, 1987.

　　［3］ ULICHNEY R A. Dithering with blue noise［J］. Proceedings of the IEEE, 1988, 76(1): 56 79.

　　［4］ VELHO L, GOMES J M. Digital halftoning with space filing curves［J］. Computer Graphics, 1991, 25(4):81 90.［5］ OSTROMOUKHOV V. A simple and efficient errordiffusion algorithm［J］. Proceedings of ACM Siggraph, 2001:567 572.

　　［6］ SHIAU J, FAN Z. A set of easily implementable cofficients in error diffusion with reduced worm artifacts［J］. Deviceindependent Color, Color Hard Copy and Graphics Arts Proc SPIE 2658, 1996,2658:222 225.

　　［7］ 张寒冰,袁昕. 数字半色调技术中的误差扩散算法的研究［J］.计算机应用,2010, 30(4): 925 928.

　　［8］ 叶玉芬,郭宝龙,马佳. 基于视觉差的误差扩散半色调算法［J］.计算机工程,2006,32(16): 195 198.

　　［9］ 田玉敏,柯丽芳,马勇. 一种改进的基于蓝噪声的误差分散算法［J］.计算机工程与应用，2006,42（26）:60 62.

　　［10］ FUNG Y H, CHAN Y H. Optimizing the error diffusion filter for blue noise halftoning with multiscale error diffusion［J］. IEEE Transactions on Image Processing, 2013, 22(1): 413 417.

　　［11］ Guo Jingming, Chang Jiayu, Liu Yunfu,et al. Tonereplacement for multitoning［J］. IEEE Transactions on Image Processing, 2015, 24(11): 4312 4321.

　　［12］ Wang Zhou, BOVIK A C. A aniversal image quality index［J］. IEEE Transactions on Signal Processing Letters, 2002, 9(3):81 84.