文献标识码: A
DOI:10.16157/j.issn.0258-7998.2016.08.020
中文引用格式: 许高斌,闵锐,陈兴,等. 一种新型超声波测距系统信号处理方法[J].电子技术应用,2016,42(8):84-86,90.
英文引用格式: Xu Gaobin,Min Rui,Chen Xing,et al. A new research of signal processing of ultrasonic ranging system[J].Application of Electronic Technique,2016,42(8):84-86,90.
0 引言
超声波测距系统以其对外界环境如雾霾天气、沙尘暴天气、雨雪天气等的高适应性而占据了绝大多数的汽车倒车雷达市场。传统的超声波换能器中心频率为40 kHz[1],传统的滤波器以及包络检测设计为RC阻容耦合电路的硬件电路实现[2],但是RC硬件电路存在不稳定性。数字滤波、数字提取包络相对于传统的模拟滤波和硬件提取包络来说,不仅省去了复杂的电路设计,而且处理信号的精确度和稳定性也都有大幅度提高。国防科技大学对回波处理算法进行了细致的研究[3-4],其主体思路是利用伪随机序列的相关运算进行处理,考虑到相关运算中FFT等运算的复杂性以及500 μs的码元长度,其并不适用于短量程的嵌入式测距系统。北京科技大学采用了基于能量重心法和最小二乘法的椭圆中心算法处理回波[5],虽然精度控制在0.2%,但是复杂的运算必须结合上位机才可以实现。国内还有很多关于高精度超声波测距系统的研究[6-8],但是并未提及信号处理的具体实现方案。针对以上设计的不足,提出了一种新型的应对嵌入式系统的超声波测距五步算法,在数字滤波的基础上采用一种新型的包络检测方式,同时在数据处理方面采用了新型的点迹计算法来计算回波峰值点。
1 超声波测距系统框架
系统框图如图1所示,实验采用主控为基于Cortex-M4的ARM芯片。系统的工作流程为:主控芯片通过发出已被编码的正负互补的PWM波形,促使驱动放大器模块输出幅值放大的正弦波。并通过中周模块的稳频,驱动超声波换能器发出中心频率为40 kHz的超声波。当超声波遇到障碍物时返回,经过前置放大电路的放大后,进入ADC模块进行数模转换,转换出的信号通过本文设计的数字通路后被解码,从而被CPU处理。

图1 系统框架图
距离可以通过式(1)计算:

式中,s为障碍物到探头的距离,v为空气中的声速,T近似为超声波在空气中的传播时间,近似程度由算法的延时决定。
2 超声波测距DSP模块设计
超声波数字通路处理从ADC的输出信号开始,实际的数字信号处理模块设计如图2所示。
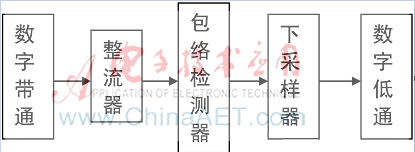
图2 五步算法框架
DSP模块的五步算法处理流程:从ADC的输出信号经过数字带通滤波器,可以滤除由于在空气中传播而掺杂的高斯噪声。为了避免包络检测的正负抵消,需加入整流器,整流器的输出需要经过峰值提取器,提取采样信号的包络,以计算准确的回波到达时间以及中断触发时间。由于1 MHz的采样率不适用于计算机对数据的运算,则需要一个下采样模块来降低采样率满足计算机的需求。下采样模块的输出信号需经过数字低通滤波器来滤除高频噪声。
2.1 IIR数字带通滤波器的设计
基于MATLAB的IIR数字滤波器的设计有多种方式,经过反复实验,在最大程度节约开发成本、保证滤波效果的情况下,确定滤波器的阶数设定为2,采用模拟滤波器通过双线性变换法转数字滤波器。为了方便ARM内核的移植,同时考虑到倒车雷达用户不需要使用C来设计滤波器,结合实际工程需要,利用MATLAB软件开发与设计滤波器,得到滤波器的传递函数参数,然后再将MATLAB中的filter函数利用C设计实现,即可以达到事半功倍的效果。图3所示为超声波回波信号与带通滤波器的输出,可以看出对于高斯噪声的抑制效果优良。
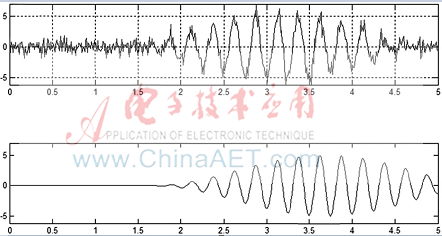
图3 回波信号及带通滤波器输出
2.2 整流器的设计
由于数字信号后期会进行包络检测,当超声波的接收波形分布在X轴的上下侧,检测出的包络会正负抵消,则无法实现预期的结果。这里的整流器可近似为一个二极管的作用,使处于X轴负半轴的信号屏蔽,以利于后期的包络检测处理。程序上可以通过将X轴下方的数据均赋0来实现。
2.3 包络检测器的设计
在超声波测距系统中,由于超声波的衰减以及超声波换能器压电陶瓷在压电转换过程中的惯性滞后导致超声波的回波信号被拓宽,使得回波到达时间点不确定,同时由于传统设计的比较器阈值固定,增大了误差的发生几率,所以包络峰值检测在判断飞越时间的过程中起着重要作用。通过MATLAB提供的库函数可以方便地提取包络,但是MATLAB库函数用C语言很难实现,而且过于频繁的乘加运算和FFT运算会增大工程算法的延时,对超声波测距带来不利影响,且不便于移植。
峰值提取新算法是利用C语言实现峰值检测,其理论依据为移位算法。如果峰值提取器的输入大于先前的峰值提取器的输出,则峰值提取器的输出被更新,其理论框图如图4所示。
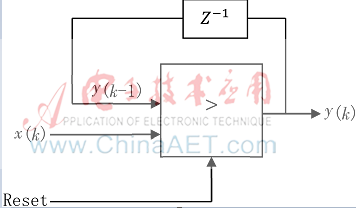
图4 峰值提取算法示意图
其中x是峰值提取器的输入,k是步长,y为输出。在波形上升部分,包络可以很好地提取,其技术难点在波形的下降部分。因为该算法只对比前一数据值更新,而对于过峰值后,波形的包络无法被该算法更新则为一条直线。考虑到短延时的存在并不过多地影响最终的时间检测,所以允许包络相对于峰值点有一定的延迟。
对下降部分单独分析,需结合下采样器的功能:对峰值提取器进行复位清0,同时生成输出。峰值提取器的输出是在下采样器中的定时器到达预定值后生成输出,即输出为峰值点后,再对该输出清零继续进行后面的比较。下采样器中的计数器的预定值,本质上就是下采样的频率缩小为原始输入频率的1/DS,DS亦为每2个输出点之间的采样间隔。该算法的仿真结果如图5所示,可见包络提取满足工程设计的需要,且节约了设计成本和减少了运算延迟。结果显示有少许的相位差,可以通过实际测距过程中的测量统计来纠正。
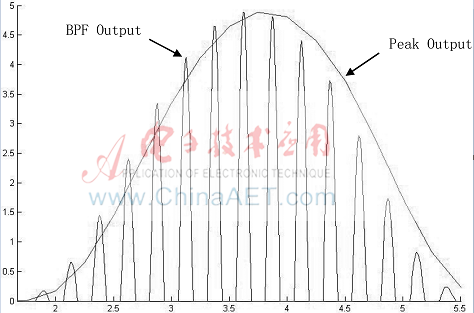
图5 峰值包络检测的新算法仿真
2.4 下采样器的设计
一个样值序列间隔几个样值取样一次,这样得到的新序列就是原序列的下采样。采样率变化主要是由于信号处理的不同模块有不同的采样率要求。下采样相对于最初的连续时间信号而言,为了防止频谱混叠要满足采样定理,此方案设计已将下采样模块与峰值提取模块进行融合和互补控制,通过下采样模块可以使最后信号的采样率与符号速率相等。这样处理获得的信噪比增益会大幅度提高。下采样方便了后面的低通滤波器的设计,这是相辅相成的。为了迎合低通滤波器的处理效果,经过反复实验分析,下采样寄存器的最佳允许值范围为25~50。
2.5 IIR数字低通滤波器的设计
IIR数字低通滤波器的设计与带通滤波器一致,本文设计的低通滤波器阶数为1,可以满足实际工程应用需求。从ADC出来的信号为幅度变化的高频信号,虽然发射的波形为等幅波形,但是在超声波信号的传输过程中受到噪声的干扰,产生了很多的高频噪声分量,导致接收到的信号为幅度变化的高频波。由于高频回波信号的包络为低频分量,加入低通滤波器可以滤去高频处的噪声,同时也可以滤除由于带通滤波器拓宽带宽而带来的噪声。低通滤波输出亦为五步算法综合输出,其输出图以及频谱对比图如图6所示,可以看出算法的平台通用性和可移植性。
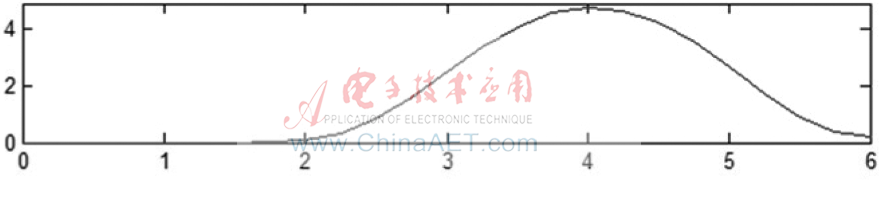
(a)低通滤波器输出

(b)C输出的频谱

(c)MATLAB输出的频谱
2.6 输出数据的处理
对于输出数组的处理,采用一种新型的结合下采样点迹的方式来计算超声波的渡越时间,这种方法可以避开定时器的使用,节约了硬件资源,避免了由比较器的误触发而导致定时器中断的干扰。同时由于数据处理的延时与渡越时间的测量是一对矛盾体,为了提高系统精度,五步算法传递的数据均为浮点数,对于不同的回波数据值,ADC以及五步算法的软件延时累积误差会达到30 μs左右,所以利用点迹计算的方式实现了时间测量与系统软件延时的有效分离。
算法处理方式如下:在低通滤波输出后,得到的包络数据被保存于数组中,可以结合传统的阈值处理以及回波包络的对称性找到回波数据中的峰值点,利用该峰值点在数组中的位置,同时根据下采样的周期t_per计算出超声波发射与接收的时间差。由于五步算法的相位差以及系统硬件的延迟与待测距离无关,为固定值,所以通过板级实验可以测试出总体的时延,在计算实际距离时将误差减去即可。
假设找到的峰值点为数组中的第N点,板级实验测试的总体时延为t_dly,则超声波发送与接收时间差T为:

将T代入式(1),再加上温度传感器的补偿反馈,即可实现测距目的。
2.7 测距算法的板级实验
为了测试所设计的五步算法的可行性,在自主设计的ARM超声波测试板中进行了板级实验。
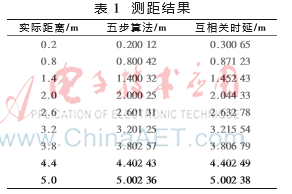
通过超声波测距系统的量程(20 cm~5 m)固定距离,并以60 cm步进,分别使用本文设计的数字通路五步算法和传统经典的互相关时延算法进行了测距性能的对比,测试结果如表1所示。可以看出,在同等测试环境下,由于码元长度的限制以及包络提取、信道噪声的影响,互相关算法在近距离时出现了较大的误差,相比之下本文算法的精确度更高。
3 结论
本文采用全数字化的五步算法实现对超声波回波信号的处理,通过MATLAB与C程序输出的对比与分析可知,设计方案合理,且便于对嵌入式主控的移植。相对于传统的硬件模拟RC处理电路的设计,本文设计的方案具有更高的稳定性与实时性,通过与互相关时延算法实验比对,本文的测距算法方案具有更高的精度,且更适用于实际工程的应用。
参考文献
[1] 张红莲.基于单片机的超声波测距系统的设计[J].可编程控制器与工厂自动化,2008,21(9):89-91.
[2] 陈云超,程晓峰,郭峰.基于FPGA控制的超声波测距系统设计[J].微型机与应用,2012,31(1):90-92.
[3] 祝琴.扩频技术在超声测距系统中的应用研究[D].长沙:国防科技大学仪器学院,2006.
[4] 潘仲明,简盈,王跃科.基于两步相关法的大量程超声波测距技术[J].电子测量与仪器学报,2006,20(5):73-76.
[5] 陈先中,侯庆文,叶琳,等.超声测距系统的高精度中心椭圆算法[J].北京科技大学学报,2007,29(11):1154-1157.
[6] 陈上挺,谢文彬,游颖敏.基于STM8的红外与超声波测距仪设计[J].电子技术应用,2011,37(9):32-34.
[7] 赵海鸣,王纪婵,刘军,等.一种高精度超声波测距系统的改进[J].电子技术应用,2007,33(4):59-62.
[8] 张禾,李俊兰,葛亮,等.一种高精度超声波测距系统的设计[J].自动化仪表,2012,33(2):62-64.

