0 引言

    古代建筑图纸能够反映古人对建筑独特的认识与理解，不仅具有极高的历史价值、文化价值和科学价值，同时也是现代仿古建筑、园林景观和旅游景区的重要借鉴^[1]。建筑图纸的质地、图形、字体及涂料具有多样性，需要特别的保护。当前，在实际的工作环境中，大部分建筑图纸以卷宗的形式进行保存，随着时间的变迁，建筑图纸的缺损非常严重，且在扫描、微缩处理中，图纸的像素丢失严重。对建筑图纸进行修复、评估及再利用，一直作为建筑学科及计算机图像处理等领域的研究热点而受到关注^[2]。僛文峰等人指出图纸的破损主要是由于图纸质地的酸性化而变黄、发干, 以及随之而来的粉碎和撕毁情况比较严重；由于时间久远，图纸质地及颜料也会出现不同程度的缺损、黄色斑点等破损；在对古建筑图纸进行信息化加工的过程中也会造成像素的丢失，出现黑色斑点等。本文针对扫描及微缩以后的古建筑图像提出一种新的基于字典学习的修复方法，该算法在稀疏域针对污损图像的特迭代处理，从而达到古建筑图纸修复的目的。通过实验表明，该算法能较好地修复古建筑图像，降低了图像的均方误差，在实际应用中具有良好的前景。

1 古建筑图像修复模型

1.1 基于稀疏表示的古建筑图像处理模型

    在图像处理领域^[3]，任一理想的古建筑图像可以表示为y₀∈R^N，稀疏表示的目标是找到一个稀疏表示向量x₀，且x₀的0范数||x₀||₀=k₀，满足：y₀=Ax₀。A为字典，B为图像退化算子，表示图像丢失掉的p个采样，则：y=By₀。B表示单位矩阵(大小为：n×n)根据丢失掉的（缺损）采样去除p行后的矩阵，其大小为(n-p)×n，则古建筑图像修复问题就转化为求其稀疏表示向量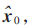进而获得未降质图像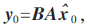则可以建模为式(1)^[4]：

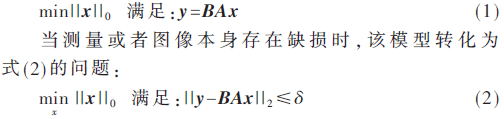
1.2 对模型的求解

    该问题中由于原始古建筑图像y₀未知，且古建筑图像一般较大，存在多种类型的缺损，因此需要对大的图像进行分块。根据给定的字典A，将大的图像分割成一些小的块后，每个块都有其稀疏表示系数，降质操作B为一矩阵，根据Elad等人的原理，该问题属于M-稀疏域模型，则可以转化如下最大后验概率问题^[5]：

    下一部分获得该模型中字典A的求解，通过式(5)能够获得输出图像，对丢失掉的像素，通过块中已知像素进行平均获得。

2 字典学习算法

    字典学习过程一般分为2个阶段，分别是稀疏编码及字典更新。在对式(5)求解时，一般假设字典A∈R^n×k(k>n)为已知，如DCT、DWT和FFT等。为了进一步提高修复古建筑图像的修复能力，本文分别通过MOD算法和K-SVD算法进行字典学习，在字典学习过程中需考虑缺损像素。因此，一旦获得字典，就可以完成稀疏编码，然后固定系数，再更新字典，从而转化为求式(6)错误的最小值：

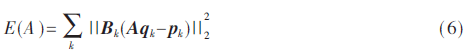
2.1 MOD字典学习算法

    MOD算法（Method of Optimal Direction）也称为最优方向法^[6]，该算法由K.Engan等人在1999年提出,通过对错误求导，然后令其为0，则可得：

2.2 改进的K-SVD字典学习算法

    本文根据缺损的古建筑图像进行K-SVD字典学习，利用K-SVD算法[7]每次更新字典A的一列，对字典的第j列a_j，根据式(6)，仅有第k块用到了这个原子，将其表示为域P_k，则可将式(6)进行如下转化：

    将图像块合并后输出即可获得最终修复图像，经过字典学习后获得的MOD字典及K-SVD字典如图1和图2所示。由图可见，K-SVD字典包含了缺损图像形变区的原子，表明K-SVD字典能够根据图像的特点进行自适应调整，从而保留更多的细节和边缘信息，更加有利于后续的处理。

2.3 算法分析

    该算法的计算复杂度可以分为两部分：稀疏编码、字典更新（迭代J次）与最终的输出过程构成。古建筑图像中的每个像素点的计算复杂度为：O(K×L×J)，其中，K为字典的列向量的个数，L为每个系数的非零元素的个数，一般取决于古建筑图像的噪声的方差和缺损像素的个数。

3 模拟实验

    对本文提出算法的性能进行测试，实验用古建筑图像称为重檐四角亭，来源于成都理工大学；图像的大小为256×256。实验所使用的PC是CPU 3.0 GHz，内存为2 GB，算法用GNUOctave进行实现。图3分别为加噪20 dB后，损失50%像素后的原始古建筑图像，以及采用MOD字典学习算法的修复结果和采用K-SVD字典学习算法的修复结果图。设置字典原子的个数为256，图像块大小为8×8。图4为随着迭代次数的增加，MOD字典学习算法和K-SVD字典学习算法的修复效果对比图。表1为采用MOD字典学习算法和K-SVD字典学习算法迭代15次后所获得的RMSE(均方根误差)。由图3可见，采用K-SVD算法修复的效果明显优于采用MOD算法修复的效果，尤其是右上角塔顶处的局部放大图所示。

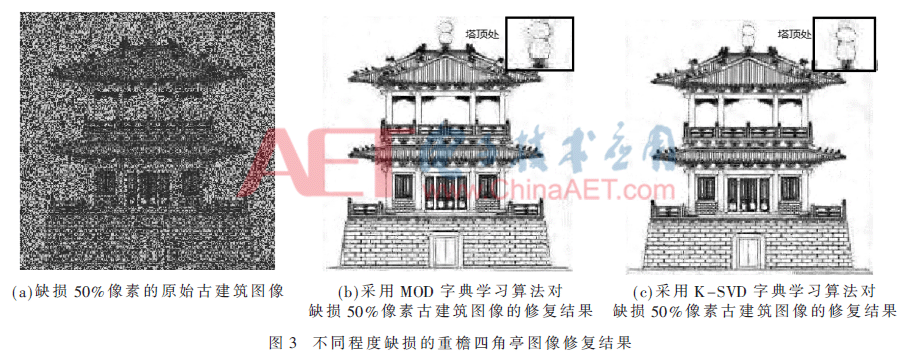
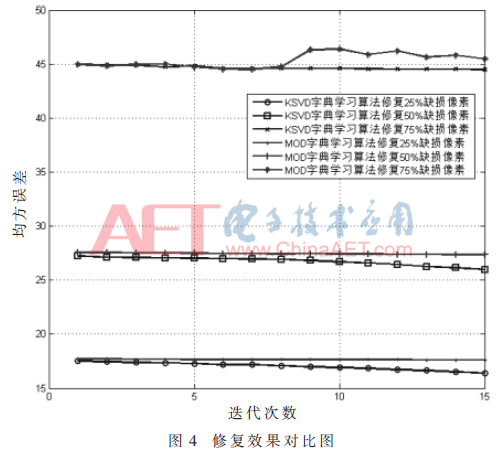
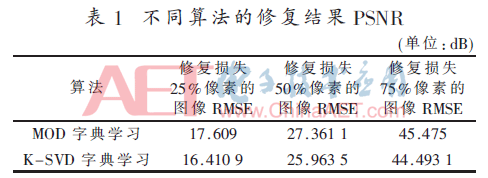
    本实验中运用K-SVD字典学习算法实现了对古建筑图像的修复，由图4可见，K-SVD字典学习算法的修复效果优于MOD字典学习算法，且 K-SVD算法的鲁棒性更强。

4 结论

    本文通过对缺损古建筑图像问题进行建模，然后利用字典学习算法实现对缺损图像的修复。通过对重檐四角亭古建筑图像进行修复试验，表明K-SVD字典学习算法具有更优的效果。本文利用机器学习及图像处理技术对解决古建筑图纸、古文献修复等问题提出了新的思路，对该算法的优化和应用的拓展是下一步研究的重点。

参考文献

[1] 王茹.古建筑数字化及三维建模关键技术研究[D].西安：西北大学，2010.

[2] 李四明.工程图纸输入与自动识别系统的研究[D].北京：中国农业大学，2000.

[3] N Metaxas D，AXEL L.Recent novel methods and approaches in sparsity-based compressive sensing and sparse learning have shown promising results. Introduction[J].Med Image Anal，2014，18(6)：819.

[4] ELDAR Y C.Compressed sensing：theory and applications[M].Cambridge University Press，2012：556.

[5] ELAD M，AHARON M.Image denoising via sparse and redundant representations over learned dictionaries[J].IEEE Transactions Image Process，2006，15(12)：3736-3745.

[6] OLSHAUSEN B A，FIELD D J.Sparse coding with an overcomplete basis set: a strategy employed by V1[J].Vision Research，1997，37(23)：3311-3325.

[7] RUBINSTEIN R，PELEG T，ELAD M.Analysis K-SVD：a dictionary-learning algorithm for the analysis sparse model[J].IEEE Transactions on Signal Processing，2013，61(3)：661-677.