0 引言

    近年来，大气环境问题越来越受到人们的关注，大气环境的污染^[1]给人们的生活带来了严重危害。与此同时，室内空气品质的好坏^[2-4]也备受重视。现代人每天有80%以上的时间在室内停留，例如据长沙市居民室内停留时间调查^[5]显示，长沙市居民平均每天约有93%的时间是在不同的室内环境中度过，可以说室内空气质量的好坏直接影响人们的身心健康。目前，室内空气质量评价方法有：空气质量指数法^[6]、灰关联评价法^[7]、模糊数学评价法^[8]等，综合指数法主要利用污染物平均值和最大值决定评价等级，当各污染物波动较大时不能正确评价室内空气质量状况，灰关联评价法和模糊数学评价法计算相对复杂。本文将改进的粒子群算法与模糊T-S神经网络相结合生成评价模型，该评价模型计算简便、分辨率高，为室内空气质量评价提供了一种新思路、新方法，并将该方法应用于智能家居室内空气质量检测与评价系统中，得到了较好的应用。

1 T-S模糊神经网络

    T-S模糊神经网络^[9]由前件网络和后件网络组成。假设有n个输入、m条规则，其拓扑结构如图1所示。

    前件网络中第一层为输入层，第二层是隶属函数层，第三层是模糊规则层，第四层是去模糊化层；后件网络中第一层同样为输入层，和前件网络第一层类似，只是多了一个常数项1的第一项输入，第二层为模糊规则层，第三层为输出层。

    T-S模糊神经网络每层计算如下：

    (1)前件网络。第二层采用高斯隶属度函数计算各输入对模糊子集的隶属度μ_ij；第三层将各隶属度进行模糊计算，采用连乘的代数运算求得模糊规则层各结点的输出w_j；第四层代表去模糊化过程，也就是归一化计算，采用权值平均判别法求得去模糊化层各结点的输出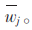

    (2)后件网络。第二层根据模糊规则求得中间层各结点的输出y_j；第三层计算整个网络的输出y。

2 PSO算法原理

2.1 基本粒子群算法

    粒子群优化^[10-13](PSO)算法是一种基于群智能的演化计算技术。设群体由m个粒子构成，粒子根据下式更新速度和位置：

其中，i=1，2，…，m；d=1，2，…，D；k是迭代次数； r₁和 r₂为[0，1]之间的随机数；c₁和c₂为学习因子；w为惯性权重；P_id和P_gd分别表示粒子群个体及群体搜索到的最优位置。

2.2 改进PSO算法

    速度更新公式(1)中 r₁和 r₂是独立的，如果两者都较大，个体经验和社会经验都会被过大使用，致使粒子远离最优值；如果两者都较小，个体经验和社会经验都不能被有效使用，致使收敛速度下降。针对这个问题，文献[14]对速度更新公式进行了改进，提出了IPSO算法。其算法位置更新公式为：

    IPSO算法公式(3)中，第一部分先前速度的系数相当于标准粒子群算法的惯性权重，sign( r₃)只有+1和-1 2个取值情况，起到调整速度方向的作用，r₂的随机性较大，可能致使粒子一直朝着最好位置的相反方向飞去，离最优解越来越远，这时的粒子群算法会需要更多的迭代来达到全局最优，且更有可能找不到全局最优。为了解决IPSO算法存在的收敛速度、收敛精度问题，本文提出新的改进PSO算法，改进的速度更新公式如下：

    式(5)中增加了自适应调节因子，式(6)为其L计算公式，当个体最优位置优于新更新的位置时，说明粒子正在远离较好解，此时让L取值为-sign(r₃)，使粒子往回调节，避免粒子离较好解越来越远；相反则让L取值为sign(r₃)，加快粒子到较好解位置，通过社会经验与个体经验差值为因子对粒子的反向进行调节，这样既能保证粒子群算法全局搜索与局部搜索的平衡，又提高了收敛速度和收敛精度。

3 改进PSO优化TSFNN算法思想

    在确定了T-S模糊神经网络后，将前件网络的模糊化层隶属函数的中心、宽度以及后件网络输入层与中间层权值组合成一个粒子。本文通过改进PSO算法对模糊T-S神经网络的各参数进行优化。

    具体算法步骤为：

    (1)初始化改进PSO优化TSFNN(改进PSO-TSFNN)算法参数，包括个体位置、速度、加速因子、最大迭代次数、学习率等。

    (2)通过TSFNN训练误差计算每个粒子的适应度值，适应度函数选取为训练样本所对应的评价输出Y_i和实际输出O_i之间的差值的平方的二分之一。因此，第i个粒子的适应度函数F_i为：

式中，s为训练样本数量，TSFNN每产生s组输出进行一次参数调整，参数调整选用梯度下降算法。

    (3)根据所得适应度值选择每个粒子所搜索的最优位置P_i和整个种群搜索的最优位置P_g。对于每个粒子，将其适应度值与其经历过的最优位置P_i进行比较，如较好，则将其作为当前的最优位置P_i；对于每个粒子，将其适应度值与全局所经历过的优位置P_g进行比较，如较好，则重新更新设置P_g；

    (4)根据式(2)、式(5)更新每个粒子的位置和速度；

    (5)检验每个粒子的速度和位置是否越界，如果越界，进行相应的阈值处理；

    (6)如果未达到预先设定的停止标准(通常设置为最大迭代次数或最小误差)，则返回步骤(2)，若达到则停止计算，利用最优TSFNN结构参数对测试样本进行最优输出。算法流程图如图2。

4 构建标准评价表

4.1 评价指标的选取及分级标准

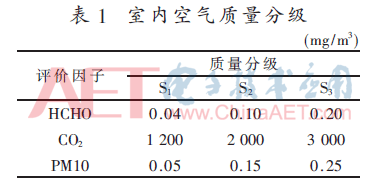
    根据《室内空气质量标准》GB/T18883-2002^[15]选取某高校实际环境具有代表性的甲醛（HCHO）、二氧化碳(CO₂)、可吸入颗粒（PM10）3个指标作为评价因子，充分考虑室内评价因子的浓度波动范围，根据GB/T18883-2002中的标准值将室内空气质量分为3个等级，其中的S₂为标准浓度限值，单位均为毫克每立方米(mg/m³)。综上，室内空气质量分级如表1。

4.2 建立标准相对隶属度矩阵

    对表1建立标准相对隶属度矩阵，计算式如下：

式中，S_ij为第i项评价指标第j级的评价标准值，R_ij为第i项评价指标第j级的评价标准值的相对隶属度(i=1，2，3；j=1，2，3)。

    最后得出标准相对隶属度矩阵为Rij为：

    标准相对隶属度矩阵中3个评价因子(甲醛、二氧化碳、可吸入颗粒)为全0时定义其标准目标输出为1，为0.38、0.44、0.50时定义其标准目标输出为2，为全1时定义其标准目标输出为3。

4.3 标准评价表的生成与分级

    为使训练后的网络模型具有良好的适应能力，且能充分反映空气质量标准各级指标标准值的意义，在标准相对隶属度矩阵中采用内插法生成更多的样本，构造出标准评价表。这里共生成包括各项指标标准值在内的201个样本，其中151个样本作为学习样本，余下50个作为检验样本。

    同时，为了能够为智能家居室内空气质量调控系统提供可靠的输出评价，进而准确地实现调节室内空气质量到较好的状态下，将室内空气质量标准值进行客观分段，表示为特级、一级和二级。特级，适合人类生活；一级，污染因子不超标，不影响人类生活；二级，至少有一个污染物超标，开始影响人的正常生活。按照标准目标输出大小分级如表2。

4.4 模型训练和检测

    将评价指标HCHO、CO₂、PM10的浓度值作为输入向量，将标准目标输出值作为目标向量，用学习样本对模型进行训练。同时，为了证明改进PSO-TSFNN模型的优越性，用TSFNN模型进行同样条件下的训练，两者的模型结构都是3-7-1，并且都采用梯度下降算法训练1 000次，学习率都是0.005，这两种网络模型在训练过程中训练误差平方和(SSE)的变化情况如图3所示。

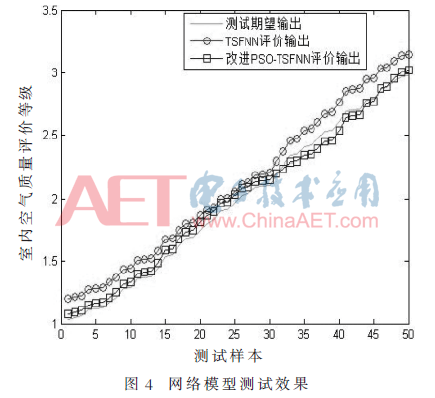
    由图3可知，改进PSO-TSFNN模型的SSE下降更迅速、终值更小、训练效果更好。训练结束后，其模型的SSE为0.000 7，而TSFNN模型的SSE为0.015 9，说明了改进PSO-TSFNN模型的学习能力更强。训练结束后，用表3中的检验样本对生成的模型进行检验，检测评价输出与实际输出如图4所示。从图4可以看出，改进PSO-TSFNN网络输出与真实的测试输出更逼近，TSFNN的测试结果误差较大。

5 实际环境评价

    本文以某实验室为研究对象，于2016年6月12日中午12点开始对其进行评价指标检测，采集频率为每秒采集1次，最后检测到当日凌晨，对数据取小时平均后如表3。

    对表3实际检测数据用改进PSO-TSFNN模型、TSFNN模型、综合指数法、模糊数学法分别进行评价，评价结果如表4。

    从表4可以看出，综合指数和模糊数学评价输出均都是一级，而从表3可知，在13:00-15:00时间段内，CO₂浓度值超出标准浓度限值，因此评价输出存在偏差；TSFNN将13:00-14:00时间段评价为一级，而从表3可知，在13:00-14:00时间段内，CO₂浓度值超出标准值浓度限值，也存在评价输出偏差；而改进PSO-TSFNN的评价输出均符合客观实际，能为智能家居室内空气质量监控调节提供可靠调节依据。

6 结语

    本文在IPSO算法的研究基础上提出了改进PSO-TSFNN模型，该模型结合了粒子群算法、模糊数学和神经网络，具有很强的模糊推理能力和并行处理能力，对粒子群算法的改进，既保证了粒子群算法全局搜索与局部搜索的平衡，又提高了收敛速度和收敛精度。通过实际环境检测数据检验了改进PSO-TSFNN模型，实验结果表明，该模型能够更客观准确的对室内环境进行评价，并且较好地应用到了智能家居室内空气质量检测与评价系统中，具有良好的应用前景。

参考文献

[1] 周桔.大气环境污染的健康效应研究回顾[J].中国科学院院刊，2013，28(3)：371-377.

[2] 张晓辉，李双石，曹奇光，等.室内空气污染的危害及其防治措施研究[J].环境科学与管理，2009，34(7)：22-25.

[3] 沈晋明.室内空气品质与健康[J].空调暖通技术，2007(2)：9-13.

[4] 兰信颖，王岳人，张浩.民用建筑室内空气品质与人体健康[J].环境保护科学，2003，29(6)：7-10.

[5] 刘建龙，谭超毅，张国强.长沙市居民在不同室内环境中停留时间的调查研究[J].制冷空调与电力机械，2008，124(29)：32-35.

[6] 邢核，李国刚.综合评价室内质量初探[J].环境监测管理与技术，2006，18(2)：35-37.

[7] 李念平，朱赤晖，文伟.室内空气品质的灰色评价[J].湖南大学学报：自然科学版，2002，29(4)：85-91.

[8] 张淑琴，白艳丽，张洪林.模糊数学在室内空气质量评价中的应用[J].环境科学与管理，2006，31(9)：188-190.

[9] KENNEDY J，EBERHARD R C.Particle swarm optimization[C].Proc.IEEE Int’l.Conf.on Neural Networks，1995：1942-1948.

[10] SHI Y，EBERHARD R C.Parameter selection in particle swarm optimization[C].International Conference on Evolu-tionary Programming.Springer Berlin Heidelberg，1998：591-600.

[11] MANGOUD M T，ELRAGAL H M.Antenna array pattern synthesis and wide null control using enhanced particle swarm optimization[J].Progress in Electromagnetics Research B，2009，17：1-14.

[12] MANDAL D，GHOSHAL S P，BHATTACHARJEE A K.Optimal design of concentric circular antenna array using particle swarm optimization with constriction factor approach[J].International Journal of Computer Applications，2010，1(17)：112-116.

[13] BERA R，MANDAL D，KAR R，et al.Application of improved particle swarm optimization technique for thinning of concentric hexagonal array antenna[C].Information and Communication Technologies(WICT)，2014 Fourth World Congress on.IEEE，2014：188-193.

[14] Qiao Junfei，Li Wei，Han Honggui.Soft computing of biochemical oxygen demand using an improved T-S fuzzy neural network[J].Chinese Journal of Chemical Engineering，2014，22(12)：1254-1259.

[15] GB/T18883-2002.室内空气质量标准[S].

作者信息:

陈双叶，徐文政，丁双春，咸耀山

（北京工业大学 电子信息与控制工程学院，北京100124）