徐文
(三峡大学 计算机与信息学院,湖北 宜昌 443000)
摘要:近年来处理边坡形变数据有很多方法,学术界较为流行的方法是把边坡体视为一个机动目标,对单条边坡体轨迹进行卡尔曼滤波平滑,来进行预测和估计。针对标准Kalman滤波观测噪声R为固定值的缺陷,本文进行了改进并对比,改进的自适应Kalman的精度得到提高,以中误差RMSE为指标分别减小了42.72%、19.70%、15.87%、16.21%,对同一边坡体多个测量点的轨迹进行融合,边坡的整体中误差下降了23.90%。
关键词: 边坡;Kalman;自适应;滤波
中图分类号:TP391.9文献标识码:ADOI: 10.19358/j.issn.1674-7720.2017.02.005
引用格式:徐文.SKF滤波与AKF滤波在边坡形变的应用[J].微型机与应用,2017,36(2):14-16
0引言
目前边坡监测的技术手段主要有四大类[1]:变形监测,物理与化学场监测,地下水监测,诱发因素监测。目前研究领域以第一类变形监测应用得最多。把边坡体的形变趋势视为一个机动目标[2]处理,Kalman 滤波是处理变形监测数据有效的一种动态数据处理方法,在变形监测领域中具有较好的应用效果[3],前人对此进行了较为广泛的研究。文献[4]提出了普通Kalman滤波对4个GPS传感器的边坡数据进行融合,对比原始数据的中误差,普通Kalman滤波之后的中误差分别得到下降。文献[5]提出了自适应Kalman滤波,效果得到了改进,但算法复杂。
1算法原理
1.1标准Kalman滤波SKF原理
将边坡监测点的位移和速度视为边坡的状态变量,则可建立滑坡在变形阶段的状态方程和实际量测方程,即动态监测模型:

在式子中,Q为状态噪声,R为观测噪声,Zk为边坡的实际位移检测值,它包含了各种影响监测的外界干扰因素(即噪声)。
1.2自适应Kalman滤波AKF原理
标准Kalman滤波的应用要求数学模型和噪声的先验知识,但在许多条件下它们是未知的。应用不精确的模型和噪声统计特性设计Kalman滤波可能会导致较大的状态估计误差,甚至可能导致滤波发散。为了克服标准Kalman滤波的上述缺点和局限性,产生了Kalman滤波理论的一个分支——自适应Kalman滤波。它解决了含有未知模型参数和噪声统计系统或含有未建模动态的系统的滤波问题。通常用噪声统计估值器或模型参数估值器伴随Kalman滤波器实现自适应Kalman滤波。利用观测数据进行递推滤波的同时,实时地对未知的或不确定的模型参数和噪声的统计特性进行适当的估计和修正,使得模型误差减小[67]。
文献[5]中提出了基于Q和R的同步自适应改进,根据自适应因子间接修正噪声。但计算量过大导致时间复杂度大为增加,如果只是对R进行改进,在加快运算速率和提高准确性之间能够得到很好的平衡。标准Kalman滤波中,当前观测值和预报状态决定了状态的估计,且主要由各自的协方差阵决定,当预报方差阵增大时,观测值中的数据更有意义,而当预报方差阵减小时,预报状态更准。那么通过动态地调节预报方差阵的大小,就能间接地影响R对状态估计的贡献,从而间接调整观测噪声。状态的预报方差阵P-k由下式得到:
P-k=αΦP+k-1ΦT+ΓQΓT
公式中,α为自适应因子,α与P-k成正相关关系,当α增大时,P-k也大,那么R的相对权重也变大,反之α减小时,R的相对权重也小。
把当前实际观测值与预报观测值的差定义为新息,公式为: εk=YK-HX-K
利用线形流形的射影方法可推导出新息序列的两条统计特性:
新息序列正交性:
E(εiεTj)=0
新息序列协方差性:
E(εkεTk)=HP-kHT+R
新息是历史信息与当前信息的综合表现,当状态模型和观测模型的统计特性准确时,新息满足以上两条统计性质,同样,由以上两条性质可反推模型的统计特性。由于新息是实时计算得到的,因而模型的统计特性也能实时地自适应修正。
利用新息的两条统计性质,可得:
![M1MAOM4]N1}8JQ19M(~MN8F.png M1MAOM4]N1}8JQ19M(~MN8F.png](http://files.chinaaet.com/images/2017/03/13/6362501617663853923344473.png)
其中新息ε由当前观测值计算得到,tr是矩阵求逆得到的[5]。
2仿真过程
本文数据集来自文献[4]。 A01~A04分别代表同一块边坡体的4个不同观测点采集到的数据,传感器型号相同,每个传感器观测点共采集了24次,每次间隔半个月,如图1~4所示。通过滤波之后,曲线得到平滑,从原始数据的折线图变成了滤波后的平滑图。
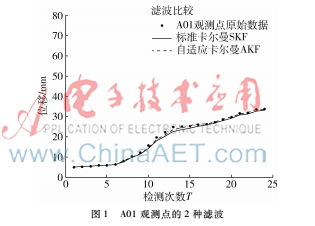
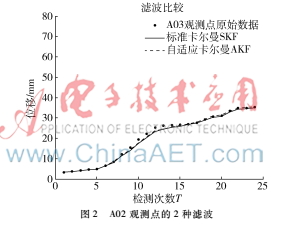
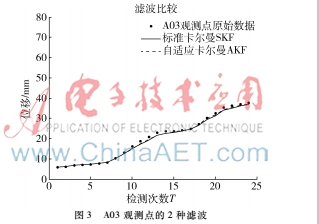

从图1~图4可以看到,AKF比SKF更加贴近真实数据,滤波效果更好。图5表示了整块边坡体的融合滤波情况。融合结果表明该滑坡体先后经历缓慢变形期、匀速变形期、加速变形期,具有阶段性变化的特点,其曲线图也符合滑坡体变形特征的自然规律[8]。

3结论分析
3.1中误差结论分析
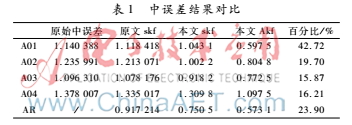
从表1可以看到,参数设置的不同,本文的标准Kalman滤波SKF比原文数据集中Kalman的中误差要低,而且通过改进算法的自适应因子调节后,自适应Kalman滤波AKF的中误差RMSE明显更低,四个传感器观测点采用的AKF滤波比本文的SKF分别减小了42.72%、19.70%、15.87%、16.21%,对其Kalman融合滤波后,AR中误差整体下降了23.90%。
3.2AKF自适应因子调整结论分析
AKF自适应因子调整结果如表2所示。
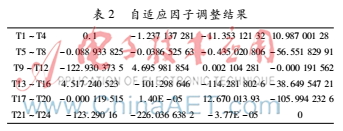
从表2可以看到自适应因子对每次滤波的调整结果,T1~T24代表24次调整,初始值设置为0.1,随着每次滤波状态的不同,每次调整的值也不同。在T9、T14、T15、T20、T21、T22处自适应因子震荡幅度较大,而恰巧在图5中可以观察到对应的这几点曲线陡峭,边坡体形变速率加快。
4结束语
本文分别使用了标准Kalman与自适应Kalman滤波对边坡数据滤波进行了对比,随着自适应因子α不断地调整,自适应Kalman滤波的效果明显优于标准Kalman滤波,得到的误差更小更准确,同时通过边坡的整体融合滤波可以得到整体误差减小了23.90%,从滤波图中可以看出形变具有阶段性变化的特征,可以推测边坡形变与外界环境因素改变存在一定联系,降雨量是一个比较重要的因素[9]。
参考文献
[1] 仝达伟,张平之.滑坡监测研究及其最新进展[J].传感器世界,2005(6):10-14.
[2] 孙波,李记刚.基于联邦Kalman技术综合提取滑坡监测信息[J].长江科学院院报,2012,29(9):39-41.
[3] 黑君淼.基于Kalman 滤波的滑坡监测数据处理与分析[D].淮南:安徽理工大学,2011.
[4] 刘超云.基于Kalman 滤波数据融合技术的滑坡变形分析与预测[J].中国地质灾害与防治学报,2015,26(12):30-35.
[5] 李洪亮,时荣.自适应卡尔曼滤波在大坝形变预报中的应用分析[J].测绘技术装备,2015,17(1):48-52.
[6] 邓自立.信息融合滤波理论及其应用[M].哈尔滨:哈尔滨工业大学出版社,2007.
[7] 邓自立.最优估计理论及其应用——建模、滤波、信息融合估计[M].哈尔滨:哈尔滨工业大学出版社,2005.
[8] 彭鹏.基于Kalman滤波融合算法的库区滑坡动态变形监测综合信息提取[J].岩石力学与工程学报,2014,33(8):1520-1525.
[9] 付杰.卡尔曼滤波在滑坡变形预测中的应用研究[D].武汉:中国地质大学,2013.

