黄增先,王进华
(福州大学 电气工程与自动化学院,福建 福州 350108)
摘要:针对维特比译码器译码过程中速度制约的问题,设计了一种结构优化的维特比译码器。该结构通过蝶形单元的直通互连,使得在状态转移过程中不需要对路径度量值进行大范围存储,简化了路径度量值的存储与读取逻辑。并且可以根据不同的应用要求灵活配置蝶形处理单元的复用次数。最后,结合FPGA平台,利用Verilog硬件描述语言和Vivado软件对译码器进行设计与实现。综合实现结果表明,该译码器占用1 564个LUT单元,能够在100 MHz系统时钟下进行有效译码。
关键词:维特比;回溯;蝶形单元;加比选;状态转移因子;FPGA
中图分类号:TN919文献标识码:ADOI: 10.19358/j.issn.1674-7720.2017.05.019
引用格式:黄增先,王进华.结构优化的维特比译码器的实现方案[J].微型机与应用,2017,36(5):6064.
0引言
在现代数字通信中,为降低数据传输的误码率,提高通信的质量及其可靠性,常在通信系统中采用纠错编码技术,其中卷积码就是一种具有较强纠错能力的纠错码[1]。由于维特比译码算法简单,易于实现,能够得到较大的编码增益,因此基于维特比译码算法的卷积码得到了广泛的应用。卷积码在编码过程中,充分地利用了各码组之间的相关性,且k和n都比较小,因此,在与分组码同样的码率和设备复杂性条件下,从理论和实际两个方面,均已证明卷积码的性能至少不比分组码差[2]。
维特比译码在算法实现过程中,蝶形单元运算需要对路径度量值按照一定的规则进行读取和存储[35],这不仅增加了存储资源的消耗还延长了译码周期。本文首先设计了一种蝶形单元直通互连的结构,基于这种结构,可以简化针对路径度量值的逻辑控制。最后,在蝶形单元直通互连结构的基础上,利用部分并行的思想对蝶形单元进行复用,设计了(2,1,7)维特比译码器,结果表明该译码器资源消耗较少。
1维特比译码算法
维特比译码算法的基本思想是利用编码网格图,在其中搜索一条路径,使其最接近实际路径,搜索到的这条路径称为幸存路径[6]。维特比译码算法实质上就是最大似然译码,它是逐步去除网格图上不可能成为最大似然路径者来搜索幸存路径[7]。维特比译码算法的一般步骤为:
(1)计算进入每一状态的各个分支度量值(Branch Metric, BM),此过程主要是比较期望码字与输入码字间的汉明距离,把这个距离称为分支度量值。
(2)把各分支度量值和前一时刻状态路径度量值相加,得到当前时刻新的状态路径度量值(Path Metric , PM)。在每个状态中,从到达这一状态的路径度量值中选出最小的那个作为当前时刻的PM。同时存储与之相应的路径作为幸存路径,这个过程称为加比选(Add Compare Select, ACS)。
(3)输入码字达到一定深度后,任选一个状态为起始状态,根据步骤(2)中所选出的幸存路径进行回溯[89]。其中回溯操作分为两个步骤,首先回溯寻找根节点,接着从根节点继续回溯进行倒序的译码输出。
图1所示的(2,1,3)卷积码网格图可以看作是由2个不同蝶形单元构成,其中S0和S2构成一个蝶形单元,S1和S3构成一个蝶形单元。假设在t时刻S0和S2的PM值分别为2和3,这时输入码字为10,则通过计算汉明距离可以得到该蝶形单元4个分支度量值从上到下分别为BM1=1、BM2=1、BM3=1、BM4=1。在t+1时刻,从上到下计算得到的路径度量值分别为PM1=3、PM2=4、PM3=3、PM4=4,最终通过比较选出t+1时刻S0状态的路径度量值为PM1=3,幸存路径为上分支路径,S1状态路径度量值为PM3=3,幸存路径为上分支路径。
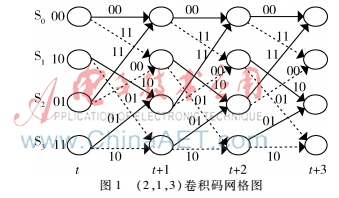
2结构优化的维特比译码电路
2.1分支度量值计算单元
分支度量值单元比较期望码字与输入码字间的汉明距离,便于之后的“加比选”单元选出该时刻的幸存路径[10]。
卷积码网格图中状态之间的转移是由卷积编码器的结构决定的,如图2所示的(2,1,7)卷积编码电路图,通过移位输入待编码字产生相应的输出并且改变编码电路中状态寄存器的值。
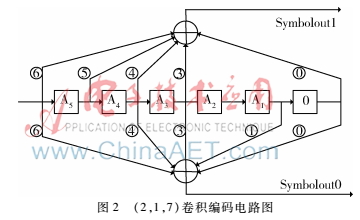
卷积码编码器状态之间的转移有一定的规则,如图3所示。

编码状态寄存器中的高五位相同的两个状态,编码输入相同的信息后状态的转移也相同,并且它们的输出也有一定的对应关系。结合图2所示的编码电路图可以看出,两个平行支路输出相同,两个交叉支路输出相同,并且平行支路与交叉支路的输出互为相反(0—1,1—0)。以状态(100000)和状态(100001)为例,具体如图4所示。

(小方块显示为编码输出)因此如果可以得到其中一个平行支路的编码输出,就可以推断出其他三个支路的编码输出。结合图2所示的编码电路和图3所示的状态转移蝶形单元图可知,蝶形单元上支路的水平输出可以通过读取状态信息获得,即Symbolout0=④^③^①,Symbolout1=⑤^④^③。得到蝶形单元的输出后只需要相应的判断就可以得到汉明距离的输出。汉明距离是表征两个码间不同位数的数量,可以用异或运算来实现,由异或运算的性质:
if (Symbolout0==1)
bm00_0=~symbolin0;
bm01_0= symbolin0;
bm10_0= symbolin0;
bm11_0=~symbolin0;
else
bm00_0= symbolin0;
bm01_0=~symbolin0;
bm10_0=~symbolin0;
bm11_0= symbolin0;
end
其中Symbolout0是编码输出,symbolin0是译码输入,再由Symbolout1的值判断另一部分的分支度量值,最后将两部分相加就可以得到完整的分支度量值。
2.2加比选单元
加比选模块主要实现的功能是将路径度量值与分支度量值相加,对结果采用二进制补码取模法(Modulo Normalization)进行尺度调整[1112]。将得到的到达同一状态的两个新的路径度量值进行比较,选出较小的那个作为下一状态的路径度量值,同时存储状态转移因子。
观察图5,每个状态转移单元中下一时刻的状态有两条路径到达,ACS单元的主要功能是比较这两条路径的路径度量值,选出较小的那个作为新的路径度量值,并给出状态转移因子。

因为前一状态只有最低位是不一样的,所以以最低位来区分,如果转移路径是由最低位为0的状态转移而来,则状态转移因子输出为0;如果转移路径是由最低位为1的状态转移而来,则状态转移因子输出为1。这样得到现态之后结合状态转移因子就可以知道这个状态的前一状态是什么,将现态值左移一位并以状态转移因子代替最后的空出位就可得到前一状态,例如:假设0A5A4A3A2A1的状态转移因子为1,则它的前一状态为A5A4A3A2A11,并且A5A4A3A2A11状态是通过输入0得到0A5A4A3A2A1,即现态的最高位代表前一状态的输入。
2.3蝶形处理单元直通互连结构
(2,1,7)卷积码有64个状态,状态转移之间对应有32个蝶形单元。图6以8状态为例来说明蝶形单元直通互连结构,具有64状态的卷积码蝶形单元的互连结构与之相似。

图6中对应8状态卷积码的3种不同译码处理方式,分别为分立的蝶形处理单元、并行互连的蝶形处理单元和部分并行互连的蝶形处理单元。分立的蝶形单元需外加存储单元对相应的路径度量值进行存储和读取,而互连的蝶形单元可以随着输入持续地进行状态之间的转移,不需要对路径度量值进行存储,从而降低译码的延迟与存储资源的消耗。如图6左边第一列的8状态转移图中分为4个蝶形单元,平行支路代表输入0,交叉支路代表输入1,用4个PE(Process Element)单元表示4个蝶形单元,分立结构需要控制PE1单元去读取PE0单元的第二个写入值PM4的同时还需要去读取PE2单元的写入值PM5,当状态数很多时,这套读取控制的复杂度随之增加,并且每个译码输入都要进行频繁的读取,功耗势必增加,同时译码延迟也会增加。图6中间一列表示并行互连的PE结构,并行互连的PE结构不需要对路径度量值进行存储与读取,通过互连结构相应的路径度量值可以正确地进入对应的PE单元。图6第三列表示部分并行互连的PE结构,通过对PE单元进行复用降低了PE单元连线的复杂度,资源消耗也降低到一半,译码速率较并行互连的PE结构略有降低。部分并行互连结构用两个PE处理8个状态转移,即一个PE单元分时处理状态之间的转移。按如下规则对部分并行互连处理单元的状态进行分配:状态标志位的最低位为0表示蝶形单元的上支路,为1表示下支路;状态标志位的最高位表示PE单元分时处理周期,0表示第一周期,1表示第二周期;状态标志位除去最高位与最低位后剩下的位表示PE序号。比如:图6中状态S5的最高位为1、最低位为1,除去最高位与最低位后为0,表示状态S5是 PE0复用单元第二周期的下支路输入。这部分难点在于如何分配输入与输出使得复用的PE模块可以流畅地运行下去。下面重点介绍PE复用机制输入输出的分配处理。
本设计输入输出分配处理应用的是同地址写回技术(Same Address Write Back)[13],即读出地址和写入地址一致,运用这种技术可以有效地减少对存储空间的占用。
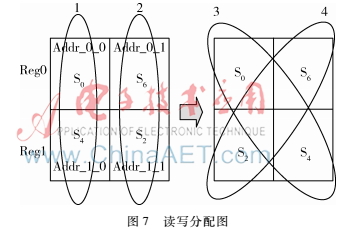
图7用来表示图6第三列中PE0的读写操作。初始化时寄存器内容为0,为方便描述,图中寄存器中写入的路径度量值直接用状态标志表示。随之译码输入按以下步骤进行:
(1)开始从上到下读取图7中第一列存储器中的值,在读取完毕后PE0模块输出到达状态S0和S4的路径度量值,利用同地址写回技术将S0和S4状态的路径度量值写回到原先被读取的空间,即从上到下写入到第一列存储器。
(2)读取第二列存储器中的值,注意此时的读取顺序是从下到上,读取完毕后将产生的S6和S2状态的路径度量值按同地址写回到第二列的存储空间中,此时同样按照从下到上写入。
(3)接着左斜着读取存储器中的值,按照从上到下的原则,读取出S0和S2的路径度量值,从而实现图6复用结构中PE0的第一列输出,同时将随之产生的S0和S4路径度量值存入原先读取的地址,同样按照从上到下的顺序。
(4)右斜着读取寄存器中的值,按照从下到上的原则读取出S4和S6状态的路径度量值,从而实现图6复用结构PE0的第二列输出,同时将此时PE0产生的S2和S6路径度量值写入原先读取的地址,同样按照从下到上。最后回到步骤(1),按照上述读写步骤循环进行下去,就可以实现图6复用结构中所示的输入输出变化。
上面讨论了8状态的PE互连结构,64状态的(2,1,7)卷积码的PE互连结构原理及规则与8状态的相似。
2.4回溯处理单元
当回溯进行到一定深度(本次设计选择为32个译码深度)确定了根节点后,就要从根节点开始继续回溯进行译码输出,输出32个译码后一个完整的回溯操作结束。所以一次回溯的深度是64个译码深度,前32个回溯深度用来确定根节点,此部分不进行译码输出,后32个深度回溯才开始译码输出。回溯操作根据状态转移因子进行一步步回溯,因此需要分配一定的存储空间对状态转移因子进行存储[14],进行回溯操作时再从存储空间读取这些状态转移因子。回溯输出的译码结果是倒序的,所以最终要对译码的结果进行倒序恢复才能得到真正有效的译码结果。

如图8,从地址64开始将状态转移因子写入存储空间中,由于PE单元的复用关系,一个时钟周期只会产生32个状态转移因子,但是64个状态一次完整的状态转移会产生64个状态转移因子,也就是整个PE模块需要2个时钟周期才能完成一次完整的状态转移。将整个互连的PE模块第一个时钟周期产生的状态转移因子存储在地址64,第二个时钟周期产生的状态转移因子存储在地址65,以此类推。所以要完成32次完整的状态转移(即32个译码深度)需要64×32 bit的存储空间,将每64×32 bit的存储空间划分为一个小存储单元。当完成64次完整的状态转移后,也就是当状态转移因子写入到地址191时,开始从S0状态进行回溯,当回溯到32深度时,即回溯到地址128或者129时,此时已经确定了根节点,接着从根节点进行回溯译码输出,当译码输出32 bit的数据,即回溯译码32个深度时,一个回溯操作窗结束。一个回溯操作窗结束之后,将回溯操作窗向前移动一个小存储单元(向前64个地址),重复上述步骤进行回溯寻根节点和回溯译码输出。
如图9所示,从地址64开始存储,互连PE模块第一个操作周期产生的状态转移因子以状态的低5位为位地址存写入字地址64,第二周期产生的状态转移因子以状态的低5位为位地址写入地址65,完成一次完整的状态转移。所以每个状态转移因子都对应一个字地址和位地址,并且第一个操作周期产生的状态转移因子的字地址为偶数,第二个操作周期产生的状态转移因子的字地址为奇数。
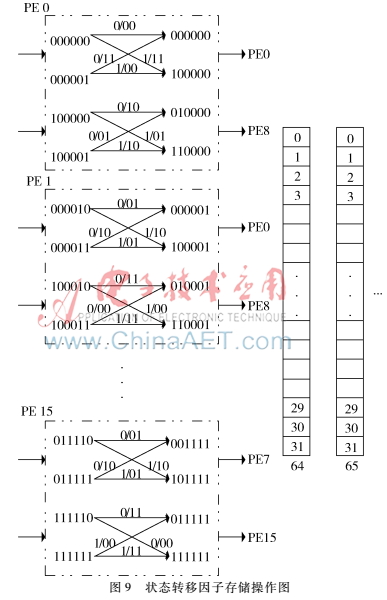
现以第一个操作窗为例描述回溯过程。在完成上述存储器的配置后回溯过程主要分为以下几个步骤:取状态字地址,取转移因子位地址,完成一次回溯操作确定前状态。
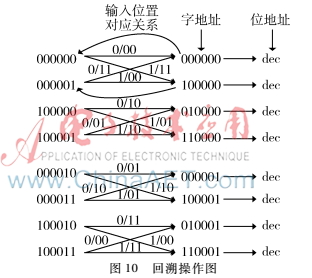
在完成64次完整的状态转移后,开始第一个回溯窗的操作(此时地址从64开始写到191)。由回溯理论知,任意状态回溯到一定深度后的根节点状态是一致的,所以每次回溯操作的起始状态设置(000000)状态。由于(000000)状态是由PE单元第一个操作周期产生的,因此它的字地址为偶数,即要读取地址190以取得状态转移因子。要读取状态(000000)对应的状态转移因子还需要位地址才可以取到,观察图10的回溯操作图,发现将位于蝶形右边的状态循环左移一位可以得到蝶形左边的状态,因此要取得相应状态转移因子的位地址,需要先将状态循环左移一位后取移位后状态的低5位即可得到。如:状态(000000)循环左移一位后变为(000000),即其对应的转移因子的位地址为0,所以依次读取字地址190、位地址0可以得到状态(000000)的状态转移因子。假如此时读取到的转移因子dec=1,将原状态左移一位用dec的值代替最低位就可以得到该状态的前态,即状态(000000)的dec=1则状态(000000)的前态为(000001),要继续回溯下去就要取得状态(000001)的字地址和位地址,将状态(000001)循环左移一位得到状态(000010),其高位为0即该蝶形是在PE模块第一个操作周期产生的,其地址为偶地址,因此在190的基础上减去2就可以得到该状态的字地址188,状态(000010)的低5位为相应的位地址2,所以从字地址188、位地址2中就可以读取到状态(000001)的转移因子。当回溯进行到32个深度后就可以进行回溯译码输出。观察图10蝶形的右端,状态的最高位表示前一状态的输入,对应蝶形的左端状态的最低位,因此可以在完成循环左移步骤后读取得到状态的最低位,该位对应的就是译码输出。
3维特比译码器电路的实现
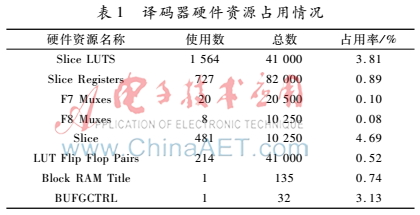
设计采用Verilog硬件描述语言对维特比译码器进行硬件描述,通过Xilinx公司的Vivado[15]进行综合与实现,并利用Xilinx xc7k70tfbg484-1 FPGA进行电路实现。在100 MHz时钟约束下建立时间与保持时间都留有裕量,说明译码器的工作频率至少可以达到100 MHz。最终,整个译码器资源占用情况如表1所示。
4结束语
本文基于蝶形单元直通互连结构,设计了(2,1,7)维特比译码器。它利用部分并行结构的思想对蝶形单元进行复用,结合同地址写回技术,简化了对路径度量值的逻辑控制,节省了存储资源。为适应蝶形单元的复用结构,设计了状态转移因子的存储结构,通过结合字地址与位地址进行读取,加快了状态回溯的速度。
参考文献
[1] 温学东. 卷积码编码及其Viterbi译码算法的FPGA实现[J]. 信息与电子工程, 2005, 3(3):176-178.
[2] 张增良. 基于FPGA的卷积编码和维特比译码的研究与实现[D]. 天津:天津大学, 2007.
[3] 黄华柱, 刘荣科, 王闰昕. 一种串行结构的2,1,7卷积码维特比译码器的FPGA实现[J]. 遥测遥控, 2009, 30(3):54-58.
[4] 韩可, 邓中亮, 施乐宁. (2,1,7)卷积码Viterbi译码器FPGA实现方案[J]. 现代电子技术, 2007, 30(15):90-92.
[5] 傅民仓, 冯立杰, 李文波. 基于FPGA的高速Viterbi译码器优化设计和实现[J]. 现代电子技术, 2006, 29(7):52-54.
[6] 元锋刚, 许海涛. 802.11b中卷积码和Viterbi译码的FPGA设计实现[J]. 无线电工程, 2012, 42(1):51-53.
[7] 林舒. 差错控制编码[M]. 北京:机械工业出版社, 2007.
[8] KAMUF M, -WALL V, ANDERSON J B. Survivor path porocessing in Viterbi decoders using register exchange and traceforward[J]. Circuits & Systems II Express Briefs IEEE Transactions on, 2007, 54(6):537-541.
[9] 王建新, 于贵智. Viterbi译码器回溯算法实现研究[J]. 电子与信息学报, 2007, 29(2):278-282.
[10] BLACK P J, MENG T H. Hybrid survivor path architectures for Viterbi decoders[C]. IEEE International Conference on Acoustics, 1993(1):433-436.
[11] HEKSTRA A P. An alternative to metric rescaling in Viterbi decoders[J]. IEEE Transactions on Communications, 1989, 37(11):1220-1222.
[12] SHUNG C, SIEGEL P, UNGERBOECK G, et al. VLSI architectures for metric normalization in the Viterbi algorithm[C]. IEEE International Conference on Communications, 1990:1723-1728.
[13] B-O M, ARG-ELLO F, BRUGUERA J D, et al. High-performance VLSI architecture for the Viterbi algorithm[J]. IEEE Transactions on Communications, 1997, 45(2):168-176.
[14] FEYGIN G, GULAK P G. Survivor sequence memory management in Viterbi decoders[C]. IEEE International Sympoisum on Circuits and Systems, 1991:2967-2970.
[15] 孟宪元. Xilinx新一代FPGA设计套件Vivado应用指南[M]. 北京:清华大学出版社, 2014.

