宋海声,吕耕耕,刘岸果
(西北师范大学 物理与电子工程学院,甘肃 兰州 730070)
摘要:提出了一种新算法,有效地减少了最近邻域法和贪婪算法在构建旅行商问题可行解过程中引入不合理长边的问题。该算法先借助一种由伪凸包算子所得到的分层模型对旅行商问题中的城市分布进行分析,之后通过将分层模型中相对外层的点逐个添加到内层的规则得到可行解。借助仿真实验求解TSPLIB标准库中的40实例,并与最近邻域法和贪婪算法进行对比,结果表明分层融合算法具有更高的精度,其平均求解质量达到8.47%。
关键词:旅行商问题;伪凸包;分层模型;分层融合算法
中图分类号:TP301.6文献标识码:ADOI: 10.19358/j.issn.1674-7720.2017.06.005
引用格式:宋海声,吕耕耕,刘岸果. 一种基于分层模型的TSP构建算法[J].微型机与应用,2017,36(6):13-15,21.
0引言
*基金项目:甘肃省自然科学基金(1606RJZA065)旅行商问题(Traveling Salesman Problem, TSP)是在1954年由美国学者Dantzig[1]提出的,是已被证明的NPHard组合优化问题[2]。由于其在邮递员投递路线选择、生产作业排序VLSI芯片设计、电路板钻孔、机器人控制、X光设备定位、电子地图和计算机网络等众多领域有广泛应用价值,因此近些年来产生了大量的关于TSP的文献。其中大多数文献主要集中于启发式算法的研究,可以分为构建型和以构建型为基础的改进型两类。比较常见的改进型算法有遗传算法[3]、蚁群算法[4]、粒子群算法[5]、免疫算法[6]、模拟退火算法[7]、禁忌搜索算法[8]等,其求解质量高,速度比较慢;而构建型算法具有简洁、求解速度快的特点。经典的构建算法有最近邻域法(the Nearest Neighborhood Algorithm, NN)[9]、贪婪算法(Greedy Algorithm, GA)[10]、插入法[9]等。
由于最近邻域法、贪婪算法和插入算法的构建结果中均含有不合理的长边,因此本文在继承最近邻域法、贪婪算法的思想后,通过建立分层模型来规避这一问题,提出了分层融合算法(Hierarchical Fusion Algorithm, HFA)。通过实验求解TSPLIB标准库中的40实例并与NN和GA算法进行对比,结果表明本文算法求解TSP具有更高的精度。
1TSP的描述
TSP可以描述为:在目标城市个数和任意两城市之间距离都已知的情况下,求解一条遍历所有城市一次且仅一次并返回到起点城市的最短线路。该问题可以用如下的数学模型描述:
设N表示城市个数,D表示距离矩阵,dij表示两城市间的距离,Inf为一足够大的正数,i,j为下标表示城市,Tour表示线路的集合,Tp(l)表示线路Tp中的第l个城市,Len(Tp)为线路Tp总长度,那么有:
![6PH15KZ)T(1H2$E(@GTF5]3.png 6PH15KZ)T(1H2$E(@GTF5]3.png](http://files.chinaaet.com/images/2017/04/08/6362729053418563398295652.png)
显然,使得Len(Tp)取得最小值的线路Tp就是TSP的最优解。根据不同的划分标准TSP大致可以分为三类:
(1)按距离矩阵是否为对称矩阵,分为对称TSP和非对称TSP;
(2)按任意3个城市间距离值是否满足三角不等式,分为三角不等式TSP和非三角不等式TSP;
(3)按城市的坐标位置是否完全符合欧几里得平面规则(两城市之间的距离可以通过坐标计算得出),分为欧几里得TSP和非欧几里得TSP。本文在未加声明时的TSP均为欧几里得TSP。
2分层融合算法
2.1分层模型
分层模型是指将问题的处理过程分解为多个具有结构相似性或功能独立性的过程。建立分层模型可以让问题的描述变得简单,并使得问题的求解过程更具条理性。本文针对TSP建立分层模型并提出以下假设:
(1)使用坐标点表示城市的位置,且所有的城市都分布在二维平面上;
(2)不存在具有相同坐标的两个点,若坐标相同则按一个点处理;
(3)任意一个点,不能同时出现在两个不同的层中;
(4)各个层必须采用相同的方式得到。
2.2伪凸包算子
本文采用伪凸包算子得到的伪凸包结构进行分层模型的建立,其步骤如下:
(1)找出剩余城市的坐标矩阵tempX和剩余城市的个数ccity,按照剩余城市的横坐标从小到大的排序得到剩余城市在横坐标方向的排序xsq;
(2)当ccity<4时,返回xsq和ccity,否则,执行步骤(3);
(3)按照剩余城市的纵坐标从小到大地排序得到剩余城市在纵坐标方向的排序ysq并取得端点西west=xsq(1),东east=xsq(ccity),南south=ysq(1),北north=ysq(ccity);
(4)初始化层layer=zero(1,N),层中城市个数cl=0;
(5)从西到北取得纵坐标增大的点并添加到layer中,更新cl;
(6)从东到北取得纵坐标增大的点并反向添加到layer中,更新cl;
(7)从东到南添加纵坐标减小且未曾添加到layer中的点到layer中,更新cl;
(8)从西到南取得纵坐标增大且未曾添加到layer中的点并反向添加到layer中,更新cl,返回layer和cl。
图1是TSPLIB标准库中att48城市的分布图。图2为分层模型所得到的att48城市分层图,其中每一条多段线表示一个层。
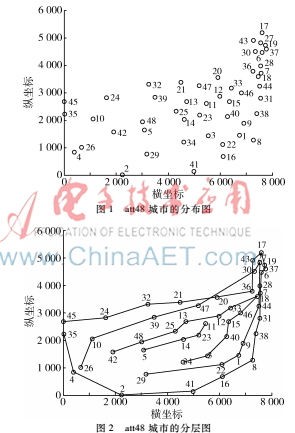
2.3分层融合算法求解TSP
本文提出的分层融合算法建立在分层模型基础之上,采用伪凸包算子得到TSP的分层模型,之后将分层模型中相对外层的城市加入到相对内层的层中完成融合。其中融合过程只限于两层之间并且是从最内层向最外层进行的。分层融合算法求解TSP的过程可以分为两个阶段:第一阶段使用伪凸包算子进行分层模型的构建;第二阶段将得到的分层模型按照融合规则进行融合求出构造解。
第一阶段:得到分层模型。
(1)初始化城市个数N,剩余城市的集合CITY=1:N,剩余城市个数ccity=N,城市坐标矩阵X。
(2)如果ccity>0,创建层记录矩阵xLayers=zeros(ccity,N)并令层个数clayers=0,跳到步骤(3);否则,提示错误。
(3)当ccity>0时,重复执行步骤(4);否则返回分层模型矩阵Layers=xLayers(1:clayers,:)。
(4)采用伪凸包算子得到一层,更新剩余城市的集合CITY,ccity,clayers++。
第二阶段:对分层模型进行融合。
(1)初始化得到第一阶段所生成的分层模型矩阵Layers和层个数clayers。
(2)当clayers>1时;重复执行步骤(3);否则,返回Layers(1,:)。
(3)分取得相对内层inlayer=Layers(clayer,:)和相对外层outlayer=Layers(clayer-1,:),利用融合规则算子将两层融合并将得到的结果赋给Layers(clayer-1,:)。
其中步骤(3)中所用到的融合规则算子详细步骤如下:
①取得相对内层inlayer、相对外层outlayer、outlayer中城市的个数coutlayer以及inlayer中城市的个数cinlayer。
②当coutlayer>0时,重复执行步骤②;否则,返回inlayer。
③随机从outlayer中选择一个点作为将要添加的点addpoint。
④当cinlayer<3时,neighbourhood=inlayer;否则,从inlayer中选择2个距离addpoint最近的点的集合作为neighbourhood。
⑤计算addpoint分别插入到neighbourhood中两点两侧时的距离增量,将addpoint插入到距离增量最小的位置,coutlayer--,更新inlayer。
3算法测试
实验求解了TSPLIB标准库中的40个实例,通过比较NN、GA与HFA三种算法的求解质量,对算法的性能进行了测试。实验平台为MATLAB 7.10.0(R2010a),CPU为AMD A83500M,内存为2.0 GB,主频为1.5 GHz。三种算法求解TSP实例的结果对比表如表1所示。其中实例名称指的是TSP的名称和该问题所包含的城市个数;最优路径长度指的是实例已知的最优路径长度;平均解和最优解分别指的是平均求解质量和最优求解质量,计算方法为:(解得路径长度/最优路径长度-1)*100%。需要注意的是,GA为确定算法,每次求出的结果都相同,所以只求解一次;而NN和HFA为不确定算法,所以进行了多次实验。当城市个数n≤100时,进行n次求解;当100<n≤1 000时,进行100次求解;当n>1 000时,进行50次求解。
由表1可知,在求解质量上NN的平均求解质量最差,为26.02%;NN的最优求解质量和GA的求解质量相当,为18%左右;本文提出的分层融合算法求解质量明显优于NN和GA。其平均求解质量和平均最优求解质量的均值分别为8.47%和4.99%,说明算法的鲁棒性和求解质量同时得到提高,相对于GR+MVODM的性能更好[11]。
4结论
本文针对旅行商问题提出了分层融合算法,借助分层模型从整体入手有效避免了经典构造算法后期引入长边的问题,从新的方向给出了旅行商问题构造解方式。该算法的优点在于求解质量高,建立了可重复使用的分层模型;不足之处在于伪凸包算子构建的层模型过于单一,各层之间进行融合时邻域制约了构造解的多样性。


参考文献
[1] DANTZIG G, JOHNSON S. Solution of a largescale travelingsalesman problem[J]. Operations Research, 1954, 2(4):393410.
[2] GAREY M R, JOHNSON D S. Computers and intractability: a guide to the theory of NPcompleteness[M].W.H. Freeman and Company, 1979.

