丁勇，卢文科，左锋

　　（东华大学 信息科学与技术学院，上海 201600）

       摘要：差动变压器式位移传感器在测量小位移量时有着许多的优点。对差动变压器式位移传感器和AD698芯片（信号调理器）的工作原理作了简单的分析介绍，利用差动变压器式位移传感器线性范围大且重复性好、灵敏度和分辨力高的测量优点，配合使用AD698芯片搭建位移测量系统，精确地将差动变压器式位移传感器的机械位移转换成单极性的直流电压。同时采用曲线拟合法构建系统的智能化非线性校正模块，进一步提高了测量系统的线性度，减小了非线性误差。

　　关键词：差动变压器位移传感器；AD698芯片；曲线拟合；智能化非线性校正；线性度

　　中图分类号：TP212文献标识码：ADOI： 10.19358/j.issn.1674-7720.2017.06.010

　　引用格式：丁勇，卢文科，左锋. 差动变压器式位移传感器测量系统优化［J］.微型机与应用，2017,36（6）：29-32,36.

0引言

　　差动变压器式位移传感器（Linear Variable Differential Transformer，LVDT）［1］在小位移量的测量中有着诸多优点，如结构简单、电路简易可靠、测量线性范围大、重复性好且线性度高、有较高的灵敏度和分辨力、价格便宜等，此外传感器内部没有活动触点，可靠性很高，使用寿命长。本文利用LVDT配合AD698信号调理系统，搭建了高效精确的差动变压器式位移传感器测量系统。

　　测量仪器系统传统功能是将系统输出的电学量转换为被测量，便于输出显示。由于测量系统输入输出特性的非线性存在，人们从电路方面出发，按某种非线性关系进行刻度转换，设计出非线性校正器来改善系统的非线性［2］。但不同传感器非线性特性的不一致性，为硬件电路的实现带来了很大的局限性。本文采用软件系统完成测量系统的智能化非线性校正模块。实现智能化非线性校正的编程方法有很多种，如查表法、曲线拟合法、支持向量机法、神经网络法等［3］。算法越复杂，软件实现难度越大，成本越高。本文考虑到测量系统的处理器性能的约束以及实现成本，采用曲线拟合法［4］实现智能非线性校正，有效且可靠。

1智能化非线性校正模块

　　1.1原理介绍

　　通过软件编程来进行非线性校正，改善系统的静态特性。

　　传感器及其调理电路的输入输出特性（x－u）称为正模型：

　　u=f(x)(1)

　　逆模型就是正模型的反非线性特性：

　　y=x=f(u)(2)

　　式中x为系统的被测输入量；u为传感器及其调理电路的输出量，也是存放在处理器中非线性校正器模块的输入；y=x是非线性校正器模块的输出，也是加入智能模块后的系统总输出。系统框图如图1所示。

　　1.2曲线拟合法实现方法介绍

　　曲线拟合法采用n次多项式来逼近反非线性特性方程，多项式方程的系数由最小二乘法来确定，步骤如下：

　　（1）进行试验标定，得到校准曲线。标定点数据：

　　xi:x1,x2,x3,…,xN

　　vi:v1,v2,v3,…，vNi=1,2,3,…，N

　　xi和vi分别为输入和输出，N为标定点的个数。

　　（2）设反曲线特性拟合方程为

　　xi(vi)=a0+a1vi+a2v2i+…+anvni

　　n的数值由精度来决定。当n=3时，

　　xi(vi)=a0+a1vi+a2v2i+a3v3i(3)

　　其中a0、a1、a2、a3为待定系数。

　　（3）利用最小二乘法来确定a0、a1、a2、a3的数值的基本思想是：多项式（3）确定的各个xi(vi)值，与各个标定值xi的均方差要最小，即：

　　为了求得函数F(a0,a1,a2,a3)取最小值时的常数a0、a1、a2、a3，将函数F(a0,a1,a2,a3)分别对a0、a1、a2、a3求导并令其为零，即得：

　　求解矩阵方程，将求得的a0、a1、a2、a3存入内存。把已知的反非线性特性拟合方程（3）写成以下形式：

　　x(v)=a3v3+a2v2+a1v+a0=［（a3v+a2）v+a1］v+a0（7）

　　为了求得对应电压为v的输入被测值x，每次只需代入式（7）进行三次(b+ai)v的循环运算，之后再加上a0。这种编程算法简单灵活且可靠。

2搭建测量系统

　　2.1LVDT原理及特点介绍

　　差动变压器主要由一个初级绕阻线圈、两个次级绕线圈阻以及一个可动铁芯组成［5］。工作过程中，在初级绕线圈阻上接入激励电源以后，次级绕阻线圈将会因此产生感应电动势。当互感量发生变化的时候，即铁芯作线性移动时，两个次级绕阻线圈中产生的感应电动势也会发生变化。在不考虑铁损图2差动变压器等效电路图、绕组分布电容以及导磁体磁阻的理想条件下，等效电路如图2所示。

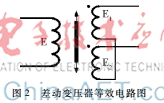
　　两个次级绕组线圈一对同名端相连，另一对同名端就可以输出与铁芯线位移量存在线性关系的电压值。

　　2.2AD698芯片原理介绍

　　AD698是一款十分完整的LVDT信号调理子系统［6］。能够以较高的可重复性和精度将原始LVDT的副边输出转换成比例直流电压。AD698芯片内部由激励源、同步比率解调以及滤波放大输出三个模块组成，结构框图如图3所示。

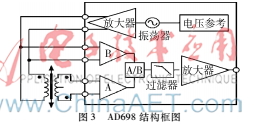
　　激励源由电压参考、振荡器、放大器构成，为外接的LVDT传感器初级绕阻线圈提供驱动功率。同步解调模块由2个相互独立、性能相同的调幅波同步解调通道A、B以及占空比除法器组成。滤波器除了滤除激励源和高频噪声的干扰以外，还将信号平滑为直流输出。放大器是一个电流放大器，占空比除法器输出的脉宽调制信号先被转换为参考电流调制信号i，i与脉冲波的占空比成正比，即：

　　i=Iref·A/B（8）

　　式中Iref=500 μA，是标定值为500 μA的参考电流。

　　电流放大器将调制的电流信号转换为电压输出信号：

　　VOUT=i·R·A/B·R2（9）

　　AD698输出电压VOUT与比值A/B成正比，也就是与被测信号（位移量）成正比，比例系数可通过外接电阻R2来设置。

　　2.3LVDT传感器侧量系统构建

　　LVDT与AD698配套使用，能够十分精确地将LVDT的机械位移量转换成单极性或双极性的直流电压。LVDT可用多种方式配接AD698：变压器次级绕组线圈反向串联、半桥式接法以及全桥式接法。本文采用的是第一种反向串联的接法［7］。配套使用的测量电路图如图4所示。

　　外部无源器件参数设置：

　　（1）激励信号e(t)的频率fEXC确定激励信号e(t)的频率,也就是说振荡器的振荡频率是由系统带宽来确定的。带宽fSUB根据被测机械位移信号x(t)的最高频率来决定，用外接电容C2、C3、C4来设置（C2、C3是解调器通道的滤波电容）。关系式为：

　　C2=C3=C4=10-4/fSUB（10）

　　fEXC的最小值应满足下面的公式：

　　fEXC=10fSUB（11）

　　外接电容C1用于设置所期望的激励频率fEXC，关系式为：

　　本文实验中，带宽fSUB设为0.25 Hz，所以

　　fEXC=2.5 Hz，C1=0.014 μF。

　　（2）激励信号幅值的确定

　　要使得LVDT处在满量程位置时初级信号有效值在1.0 V~3.5 V之间，同时次级信号有效值要在0.25 V~3.5 V之间，因为这是线性度与无噪声灵敏度的最佳区间。这又与LVDT的灵敏度S以及传感器中变压器的变比VTR有关：

　　式中Vpri、Vsec分别是LVDT在满量程位置时，变压器初级输入和次级输出电压信号。

　　LVDT的灵敏度S在数值上表示单位位移时，在初级输入信号为1 V的情况下次级输出信号的电压值（V），表达式为：

　　式中VTR可由实验测得，d为LVDT传感器的满量程输入，即铁芯偏离零点位置的最大长度。本实验传感器灵敏度S为2.4 mV/V/mil。

　　LVDT最佳激励电压VEXC的确定如下：

　　本实验中VTR测为0.48。因而可以计算得：d=±0.2 inch=±200 mil。在最佳激励电压VEXC=Vpri=3.5 V时，最大的次级输出电压为：Vsec=3.5×0.48=1.68 V，在最佳范围内。根据激励源信号的幅值Em=VEXC选择电阻R1，关系为：

　　12 V≤VEXC≤24 V,0.1 kΩ≤R1≤1 kΩ

　　5 V≤VEXC≤12 V,1 kΩ≤R1≤10 kΩ

　　2.5 V≤VEXC≤5 V,10 kΩ≤R1≤100 kΩ

　　（3）满量程输出电压VOUT的确定

　　电阻R2用来设定输出级电流放大器的增益，从而设置满量程输出电压VOUT，结合式（9）、（13）、（14）得：

　　实验设定电压幅值VOUT=±10 V，带入数据计算可得：R2=41.7 kΩ。图5位移与电压关系曲线

　　进行试验，铁芯朝一个方向移动，每移动0.500 mm记录一次数据，每组数据是多次测量值的平均值。由此得到位移与电压关系曲线如图5所示。

3智能化非线性校正结果演示

　　（1）在之前的测量数据中，选取适当的标定点。数据如表1所示。

 （2）建立逆模型表达公式：

　　X=a0+a1V+a2V2+a3V3（17）

　　（3）根据式（4）、（6）求系数：a0=5.182 663,a1=0.354 056,a2=-5.821 352×10-4,a3-3.129 17×10-4。

　　计算上述常系数值的式（17）的编程算式在本实验中存入智能化非线性校正模块中实现。

　　（4）逆模型检验。向逆模型中输入电压V，比较实验值的位移量X与逆模型计算值X′，其偏差Δ=|X－X′|。结果如表2所示。

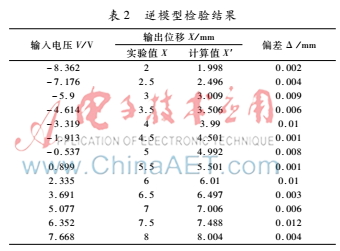
　　(5)线性度改善情况分析。

　　①利用最小二乘法可得正模型的拟合直线方程：

　　V=2.712X-14.085（18）最小二乘法线性度计算公式：

　　δL=|ΔLm|Y(FS)×100%（19）

　　本实验在2.000～8.000 mm的输入范围中，拟合偏差的最大值ΔLm=0.299 V。

　　Y(FS)=V(X=8.000)－V(X=2.000)=16.272，所以得到改善前系统线性度：

　　δL=0.29916.272×100%=1.84%

　　②改善后系统的拟合直线可以选为理想直线方程：X=kX,k=1。由表2可知最大的拟合偏差为0.012 mm,Y(FS)为标定量程6 mm，所以改善后系统理论线性度为：

　　δ′L=0.0126.000×100%=0.2%

　　与改善前的相比，系统的线性度得到了明显的提升。

4结论

　　LVDT配合AD698搭建的测量系统，加入智能化非线性校正模块，更进一步提高了测量系统的线性度，降低了非线性误差。采用的曲线拟合算法在程序实现上灵活简便且可靠。

　　参考文献

　　［1］ 张建.传感器与检测技术［M］.北京:高等教育出版社,2002.

　　［2］ 刘君华,智能传感器系统（第二版）［M］.西安:西安电子科技大学出版社,2010.