赵柏山,肖乃瑶,张学松
(沈阳工业大学 信息科学与工程学院,辽宁 沈阳 110000)
摘要:图像匹配对于工具识别过程具有重要意义,传统的图像匹配算法匹配过程复杂导致匹配速度慢,在实际应用中有局限。为了提高工具识别的效率,通过分析工具图像特征,设计出一种基于Harris角点特征的图像匹配方法进行工具识别。首先用Harris算法提取工具模板图像与搜索图像角点特征,然后使用归一化互相关匹配算法计算工具模板图像与搜索图像角点特征的相关值,进而确定匹配点对,最后采用RANSAC去除错误匹配点对。通过实际数据验证,基于Harris角点特征的图像匹配方法与传统方法相比,不仅识别速度快,鲁棒性好,而且在实际工程应用中更具适用性。
关键词:图像匹配;工具图像特征;工具识别;Harris角点特征;归一化互相关
中图分类号:TP391文献标识码:ADOI: 10.19358/j.issn.1674-7720.2017.06.014
引用格式:赵柏山,肖乃瑶,张学松. 基于Harris角点匹配的工具识别方法[J].微型机与应用,2017,36(6):43-45,50.
0引言
*基金项目:辽宁省教育厅一般研究项目(L2014053)图像匹配[1]是指在空间上相同对象的两幅或更多幅图像的配准。图像匹配的技术过程称为图像匹配。图像匹配是应用非常广泛的图像处理技术,图像匹配在地图与地形分析、医学图像研究、机器人视觉等多领域有重要的应用价值,国内外很多学者在图像匹配方面也做过很多研究,其研究对象各不相同,至于工具的识别方面,尚未有一种普遍使用的方法解决其匹配问题。
近些年来图像匹配算法始终是人们探究的热点,通常图像匹配的方法[26]可以分为两大类:基于灰度的图像匹配方法和基于特征的图像匹配方法。经典的灰度图像匹配方法有:序贯相似性检测(Sequential Similarity Detection Algorithm,SSDA)和对应像素差的平方和(Sum of Square Difference,SSD)等。基于灰度的图像匹配方法具有精度高的优点,但是匹配速度慢,对灰度变化、旋转、缩放十分敏感。基于特征的图像匹配方法有两个重要的环节:特征提取和特征匹配,可以选取的特征包括:点、线、与区域,其中点特征最常用,经典的点特征提取算法有:Harris算子[7]、SUSAN算子[8]和Canny算子[9]等。基于特征的图像匹配方法可以改善基于灰度的图像匹配方法的缺点,从而在图像匹配方面得到了广泛的应用。
本文通过分析工具图像特征,采用基于Harris的算法进行角点的提取并用归一化互相关匹配算法进行工具匹配识别,该方法有效地提高了工具识别的效率。
1基于Harris角点的工具识别
1.1工具图像特征分析及角点提取方法
迄今为止,图像特征还没有一个准确的定义。理想的图像特征描述符应该是:可区分、丰富以及高辨别率等。在工具识别匹配过程中,工具图像有如下特征:
(1)背景简单;
(2)形状特征信息丰富;
(3)角点特征明显。
角点信息中包含了大量内容丰富的局部特征和形状特征信息,在角点提取过程中提取方法较多,常用的方法有Moravec算子、Harris算子等。
Harris角点提取算法由HARRIS C和STEPHENS M于1988年提出,是对Moravec角点提取算法的扩展。Moravec角点提取算法由于没有对图像进行抗噪处理,所以不能找到所有的角点,对噪声特别敏感。Harris算子是根据图像角点处的自相关函数的关系测试的。而局部图像的灰度变化程度也是通过自相关函数描述的,如下公式所示:
E(x,y)=∑w(u,v)[f(x+u,y+v)-f(u,v)]2(1)
式中,w(u,v)表示工具特征图像窗口,E(x,y)表示由于工具特征图像窗口移动而造成的图像灰度的变化,f则表示图像的平均灰度值。由于微分算子可以显示像素点各方向的灰度变化的特征,因此用微分算子再次定义公式能够有效区分角点,公式(1)是在像素点(u,v)处展开,将E(x,y)推导成泰勒多项式的形式:
E(x,y)=∑w(u,v)[xX+yY+O(x2,y2)]2
=Ax2+2Cxy+By2(2)
上式中的A,B,C系数可以分别看作是二阶方向微分的近似值。Harris算子利用高斯函数对图像先进行平滑处理以提高抗噪能力,即算子的检测窗口采用的是高斯函数,在上面平滑操作的基础上再根据以下公式提取角点,即:
w(u,v)=exp(-12(u2+v2)/σ2)(3)
A=X2w,B=Y2w,C=(XY)w(4)
Harris角点提取算法的响应函数定义为:
R=Det(M)-κ(Tr(M))2=AB-C2-κ(A+B)2(5)
其中,Det(M)表示矩阵的行列式,Tr(M)表示矩阵的迹;κ为默认常数,通常取值为0.04。R为角响应函数值,R值越大,则该像素点的位置是角点的可能性越大,如果R值较小,则该像素点应该对应图像的工具或背景区域。
1.2工具识别
为了实现工具的快速匹配识别,并且体现工具图像特征在匹配过程中的应用,本文采用归一化互相关算法进行工具图像匹配识别。归一化互相关算法是一种经典的匹配算法,其主要应用于基于灰度的模板匹配,通过计算模板图像与匹配图像两个图像的相关值,来确定匹配程度。本文将此算法用于计算工具模板图像提取的角点特征与工具搜索图像提取的角点特征的相关值,从而确定匹配点对。工具图像匹配识别的大体步骤如下:
(1)对工具模板图像与搜索图像进行均值滤波处理。
(2)利用步骤(1)中结果,产生归一化互相关矩阵。
(3)根据产生的归一化互相关矩阵,计算工具模板图像中一角点与工具搜索图像一角点的相关值及相应索引。
(4)判断步骤(3)中结果,如果两图像对应角点索引一致,则为一对初始匹配点。
(5)重点步骤(4)求出一一匹配点。
经过上述角点匹配后,可以找出所有匹配的角点对,其中包括正确的匹配点对与错误的匹配点对,为了提高工具图像的匹配精度,利用RANSAC算法对工具图像特征点对去除错误匹配点对,从而提高匹配正确率。
2工具识别实验结果
本文的实验环境为CPU Intel Core i3370,主频2.93 GHz,内存2 GB,操作系统Windows 7旗舰版,开发环境为MATLAB 7.0。
为了验证基于Harris角点特征的图像匹配方法的有效性、适用性及合理性,分别对不同工具图像进行多次匹配实验,本文选取了部分典型实验结果,如图1、图2和图3。每幅图中(a)为工具搜索图像角点提取图,(b)为工具图像匹配结果,左边是工具模板图像,右边为工具搜索图像。
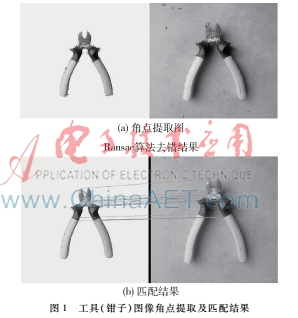
图1为工具(钳子)图像角点提取及匹配结果,验证了本文方法的有效性;图2为加椒盐噪声的工具(扳子)图像角点提取及匹配结果,验证了本文方法的适用性;图3为两个不同工具图像匹配失败结果,与前者对比,验证了本文方法的合理性。工具图像匹配数据如表1。
本文还应用基于灰度的传统算法进行工具识别,主要是与本文方法进行对比比较。表2为工具图像分别应用传统算法和本文算法进行50次匹配的实验数据。



3结论
本文介绍了基于Harris角点特征的匹配方法,经过以上实验结果分析,证明了与传统算法相比,本文算法在同样匹配精确度下有更快的速度,对含有噪声的工具图像匹配问题同样具有适用性并且也能很好地进行检测与匹配。与此同时,本文算法也存在局限性,当模板工具图像角点特征不明显时,也可能导致匹配失败,在今后的研图3不同工具图像角点提取及匹配失败结果
究中还应逐步改进,以进一步提高实时性。
参考文献
[1] 王志明, 殷诸成, 曾慧. 数字图像处理与分析[M]. 北京:清华大学出版社, 2012.
[2] 赵启. 图像匹配算法研究[D]. 西安:西安电子科技大学, 2013.
[3] BROWN L G. A survey of image registration techniques [J]. Southern Economic Journal, 1950, 17(1):20-24.
[4] 桑智明. 几种基于灰度的图像匹配算法研究[D].天津:南开大学,2011.
[5] 陈天华. 基于特征提取和描述的图像匹配算法研究[D]. 广州:广东工业大学, 2016.
[6] Wu Yue, Ma Wenping, Gong Maoguo, et al. A novel pointmatching algorithm based on fast sample consensus for image registration[J]. IEEE Geoscience & Remote Sensing Letters, 2015, 12(1):43-47.

