邱立英,林丽群

　　（福州大学 物理与信息工程学院，福建 福州 350116）

       摘要：针对医学中血细胞图像研究中粘连细胞难以分割的问题，提出一种基于主凹点检测的分割算法。通过滤波预处理去除图像的噪声以改善图像质量，基于改进的活动轮廓模型初步提取细胞轮廓，通过寻找主凹点的方法准确定位粘连细胞凹点位置，标记并融合细胞图像轮廓、粘连形状等特性，实现粘连细胞分离。实验结果表明，该方法具有很好的分割准确度和完整度，且该算法具有普适性。

　　关键词：血细胞图像；粘连细胞分割；活动轮廓模型；凹点检测

　　中图分类号：TP391.4文献标识码：ADOI： 10.19358/j.issn.1674-7720.2017.07.013

　　引用格式：邱立英,林丽群.基于主凹点检测的血细胞图像去粘连分割算法研究［J］.微型机与应用，2017,36（7）：43-45.

0引言

　　随着计算机模式识别技术及人工智能研究的不断发展，计算机在医学图像处理中发挥了越来越重要的作用，它为准确、方便、定性、定量地识别不同类型的血细胞提供了新的手段，使得图像分析逐步成为细胞学定量分析研究的有力工具。由于染色条件、涂片制备、图像来源、采样光照条件的差异以及细胞间相互重叠、粘连情况的发生，使得对血细胞的计数和识别等后续分析变得困难。

　　细胞图像分割是近年研究的热点，随着国内外学者的不断研究，已经涌现了多种多样的细胞分割方法。当细胞无粘连各自独立时，直接简单有效的分割方法有边缘检测算法（Sobel、Canny、Prewitt等）、区域增长分割算法和阈值分割算法。文献［1］为了更加准确地区分显微细胞图像的细胞浆、细胞核及它的背景区域，采用了多阈值分割的算法。文献［2］结合了分水岭法、K均值聚类和区域增强的方法对细胞图像进行分割并检测其边缘。方红萍等人［3］提出了一种基于自适应Hminima的改进分水岭堆叠细胞分割方法，该方法利用h值Hminima变换抑制种子噪声，然后基于形状先验定义圆度指标FuzzyR自适应提取堆叠区域最优h值，实现正确分割。王鑫等人［4］提出一种新的基于数学形态学运算的迭代腐蚀方法，算法的创新点之一在于为了保证整个迭代腐蚀过程，细胞种子点不会被错误地腐蚀掉，该算法能较好地解决距离变换方法中的过分割问题以及改善极限腐蚀方法中的欠分割问题。在凹点检测领域，吴宇翔［5］等人提出以模糊聚类方法来分割医学图像。文献［6］提出基于距离地形图分水岭变换分离粘连细胞。方艳红等［7］人为实现连续腹腔影像图像分割的实时性和准确性,提出多图像融合的水平集图像分割模型。

　　本文结合以上算法的优劣势以及血细胞图像形态特征等，提出了一种基于主动轮廓模型和主凹点检测相结合的算法。

1粗分割

　　1.1基于区域的轮廓模型

　　给定图像I，需要找出其轮廓C，将图像分割成相互独立的区域。Kichenassamy［8］将该类问题转换成公式表示，并提出了能量函数F1表达式：

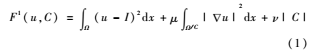
　　其中,u是原始图像的近似，|u|是u的梯度，μ和ν是两个相关系数，根据公式要得到这个函数的极小值是很困难的。Tony［9］为了解决Kichenassamy的问题提出了特殊情况下的活动轮廓能量函数F2，当u在式(1)中是一个分段常数函数时，有：

　　Chan和Vese［10］提出了分段函数F3以减小计算量，把能量函数分成4部分的和：

　　这里C1和C2是两个水平集函数，而c=(c11,c10,c01,c00)是一个常数向量，每一个元素代表对应每个区域的强度近似值。为了让模型可以有更快的处理速度，Li［10］依据F3提出了基于区域延展能量函数F4：

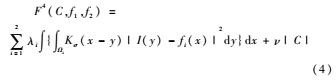
　　在式(4)中Ω1=outside(C)，Ω2=inside(C)，而f1(x)和f2(x)是每个区域的近似，K是核函数，通常是符合高斯分布的：

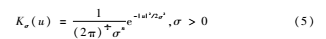
　　1.2细胞分割轮廓模型

　　在细胞分割中，可以利用细胞的结构来构造主动轮廓模型的能量函数，本文在式(4)、式(5)的基础上，提出了新的能量函数F：

　　式(6)中，C1是细胞质和背景的边界，C2是细胞质和细胞核的边界，IG是原图像与梯度图像的合成图像，f1和f2分别代表细胞质、细胞核原图像的近似图像和背景近似图像，g1和g2是IG的近似图像。在算法实现过程中，可以将整个流程变为先进行滤波再进行水平集演化的分割过程。

2细分割

　　2.1粘连细胞判断

　　细胞粘连的情况大体可分为三类:并联、串联和串并联。如图1所示。

　　如何判断图像中细胞有没有存在粘连情况是分离粘连细胞的基础。本文提出一种基于形状因子的判别方法来判断细胞有没有存在粘连情况。在粘连的区域会产生深浅不一的凹面，形状因子可以用来定义细胞轮廓的复杂程度，公式为：

　　PE=4Aπ/C(7)

　　式中，C是物体的周长，A是物体的面积。形状因子的取值范围是0<PE≤1。当物体接近圆形时，物体的形状因子接近于1，当物体的形状是狭长类型，PE的值就会趋近于0。

　　2.2主凹点检测

　　细胞图像一般表现为凹图形的特征。本文算法的基本原理是：首先搜索出细胞边缘所有的局部凹点，接着根据凹面区域的类别对局部凹点进行分类，通常一个凹面区域对应一个局部凹点类，最后从局部凹点类中确定中间的点作为此凹陷区域的主凹点。

　　具体实现步骤如下：

　　(1)选取细胞边缘上的一个点pj；

　　(2)判断其是J（水平）方向变化的像素点还是I（竖直）方向变化的像素点；

　　(3)根据步骤（2）判断的方向，在pj的8邻域内的I方向或J方向搜索与其相邻的一个点pj+1或pj-1，若没有相邻点，返回步骤（1）；

　　(4)判断是否搜索到第h点，若没有，再以pj+1或pj-1为起点，返回执行步骤(2)，若已搜索到第h点，执行步骤(5)；

　　(5)连接点pj+h和pj-h，计算直线在粘连细胞外部比例，若大于等于60%，则pj为凹点，否则pj不是凹点；

　　(6)判断是否遍历边缘的所有像素点，若是，结束；否则返回步骤(1)。

3实验结果

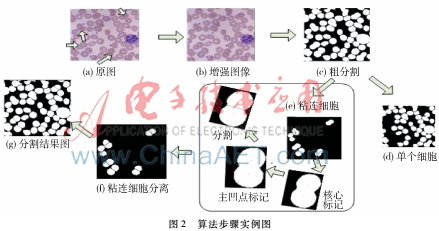
　　图2展示的是本文处理血细胞图像的整个步骤。图3给出了本文与传统分割算法的对比图。从图中可以很直观地看出，本文算法拥有更好的分割效果。分割准确率可由如下两个统计量：灵敏度(sensitivity，SS)和特异度(specificity，SC)来评估，实验数据显示，平均值SS=0.894，SC=0.901。

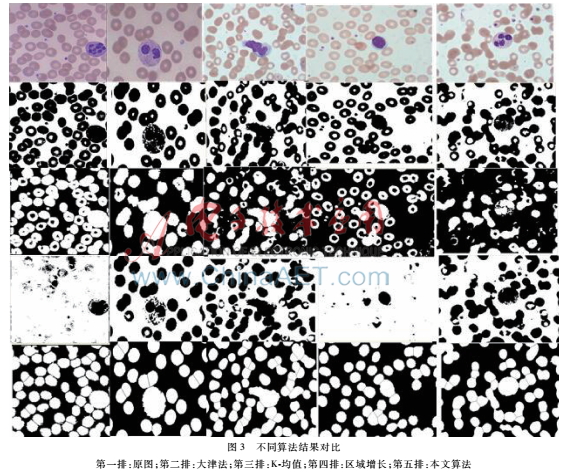
4结论

　　本文基于主凹点检测的方法，结合活动轮廓模型，实现了对血细胞图像的分割，最终的分割结果在保证准确分割的同时，也证明了所使用算法的性能较传统分割算法有更大的提高，为后续医学图像更深入的分割与分析提供了条件。

参考文献

　　［1］ GOCLAWSKI J， SEKULSKANALEWAJKO J， ANIOL P. A segmentation method for microscope images of BY2 tobacco cells in suspension cultures［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010,10(4):1921960.

　　［2］ SALMAN N H. Image segmentation based on watershed and edge detection techniques［J］. The International Arab. Journal of Information Technology,2006,3(2):104-110.

　　［3］ 方红萍, 方康玲,刘新海. 自适应Hminima的改进分水岭堆叠细胞分割算法［J］. 计算机应用研究， 2016,33(5):1587-1590.

　　［4］ 王鑫,胡洋洋,杨慧中. 基于迭代腐蚀的粘连细胞图像分割研究［J］. 南京理工大学学报，2016，40（3）：285-289.

　　［5］ 吴宇翔,龚涛,梁文宇.基于改进的免疫模糊聚类方法的医学图像分割［J］.微型机与应用,2016,35(6):51-53.

　　［6］ CONG P S, SUN J Z. Application of watershed algorithm for segmenting overlapping cells in microscopic image［J］. Journal of Image and Graphics, 2006,11(12):1781-1784.

　　［7］ 方艳红,王梁.多图像融合的连续腹腔影像图像分割［J］.电子技术应用,2014,40(8):126-127.

　　［8］ KICHENASSAMY S. Gradient flows and geometric active contour models［C］. Proceedings of 5th International Conference on Computer Vision, 1995: 810-815.

　　［9］ TONY C,LUMINITA V. Active contours without edges［J］.IEEE Transactions on Image Processing, 2001,10(2):266-276.

　　［10］ Li Chunming, KAO C Y, GORE J C, et al. Minimization of regionscalable fitting energy for image segmentation［J］.IEEE Transactions on Image Processing, 2008, 17(10): 1940-1949.