谢宇迪,蒋新昕
(辽宁师范大学 数学学院 ,辽宁 大连116029)
摘要:给出一类在非均匀节点情形下带参数的三角B样条基函数,讨论了这类基函数的性质以及在重节点情形时的变化,并利用这类基函数构造了相应的三角B样条曲线,这类曲线具有与二次非均匀B样条曲线相似的性质。在控制顶点不变的情况下,可以通过改变形状参数取值来调节曲线的形状。此外,它还能精确表示圆、椭圆等曲线。
关键词:非均匀B样条;基函数;曲线设计
中图分类号:TP391文献标识码:ADOI: 10.19358/j.issn.1674-7720.2017.07.014
引用格式:谢宇迪,蒋新昕.非均匀节点情形下的一类三角B样条曲线[J].微型机与应用,2017,36(7):46-49.
0引言
三角样条曲线在计算机辅助几何设计中被广泛地应用[1],SCHOENBERG I J[2]首次提出三角样条的概念, 韩旭里教授在三角样条函数的研究中,提出并讨论了分段的二次三角多项式曲线、三次三角多项式曲线及带有参数的二次三角多项式曲线[35]的性质和应用 ;文献[6]提出了k(k≥2)阶的带形状参数三角多项式均匀B样条曲线,可以精确表示圆、椭圆等一些曲线;文献[7]提出了带多形状参数的非均匀三角多项式曲线,它是同类型单形状参数曲线的推广。
本文给出了另一类基于四点分段的带参数非均匀二次三角B样条曲线,当所有节点等距时,此类曲线即成为文献[8]中的均匀二阶三角B样条曲线,对于给定控制点,利用参数的不同取值可以局部或整体地控制曲线形状,而无须通过改变控制点调整曲线的形状,此外,还给出了该曲线表示椭圆和圆的方法。通过实例表明,所给曲线具有结构简单、使用灵活的优点,为曲线设计提供了一种有效的方法。
1带形状参数二阶三角B样条基函数
定义1任给节点u0<u1<...<un+4,Δui=ui+1-ui,称U={u0 ,u1,...un+4}为节点向量,设-1≤λi,μi≤1,则称:
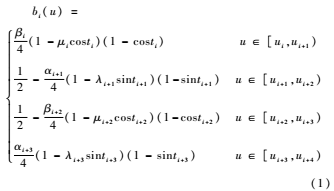
为第i个带形状参数μi,λi+1,μi+2,λi+3的非均匀二阶三角B样条基函数。其中
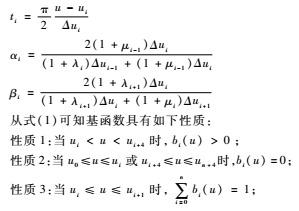
性质4:在实际应用中有时需要利用重节点技术,与单形状参数情况类似,当基函数的节点重数k≤4时,这时只要把对应的区间缩小为0,并去掉基函数的相应段即可。例如当ui+3=ui+4时,Δui+3=0,进行如下定义:
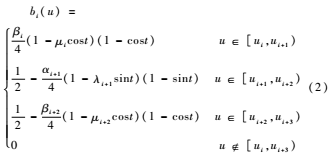
容易证明重节点时多形状参数的基函数的连续性有如下定理:
定理1如果u=uj是基函数bi(u)的k(k=2,3,4;j=i+1,i+2,i+3,i+4)重节点,则基函数的支撑区间从4减少为5-k段,k=2,3时基函数连续,k=4时不连续。
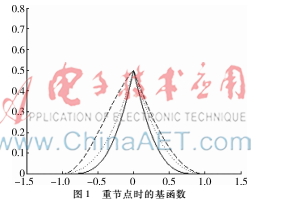
图1表示重节点时的基函数,这里的节点u=0为三重节点,可知由于参数的取值不同,多形状参数的二次三角多项式基函数(虚线)呈现不对称,单形状参数的基函数(实线)对称。
2基函数的连续性
定理2设节点向量U={u0 ,u1,...un+4}满足u0<u1<...<un+4,则由式(1)定义的基函数bj(u)∈C1(-∞,+∞)。
证明:显然bi(u+i)=0,b′i(u+i)=0,bi(u-i+4)=0,b′i(u-i+4)=0,这里仅讨论在u=ui+1处的连续性,在u=ui+2,u=ui+3处可以采用同样的方法处理。
 所以该定理的结论成立。
所以该定理的结论成立。
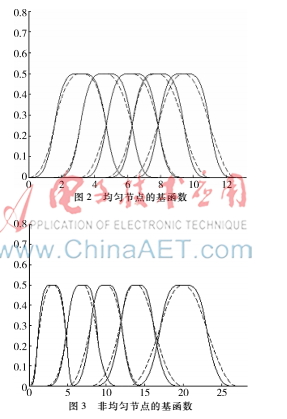
图2表示均匀节点下的基函数的图像。其中实线表示形状参数λi=μi=1时 ,即单形状参数的情形;虚线表示均匀节点下多形状参数的基函数图像,虚线对应的λi=(0.4,1,1,0.8,0.3,0),i=1,2,3,4,5 ;μi=(0.5,0.8,0.2,0.4,0,0.1),i=0,1,…4。
图3表示形状参数λi、μi对非均匀节点的基函数的影响。其中节点向量为U={0,2,5,6,8,12,13,15,20,27},实线表示单形状参数的基函数图像,虚线表示多形状参数的基函数图像,形状参数的取值与图2相同。由此可见,多参数对基函数的影响使其左右发生变化,故可作局部调控。
3二次三角B样条曲线
定义2任给R2或R3中的控制点p0,p1,...pn,节点向量 U=(u0,u1,...,un+4)及形状参数-1<λi,μi≤1,则:

称为多形状参数的二次非均匀三角B样条曲线,其中bi(u)由式(1)所定义。 当ui<ui+1(i=2,3,…n)时,曲线r(u)对应于[ui,ui+1]上的一段曲线可以表示为:
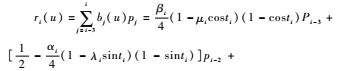
![2R9RJ]4(3DD(B@@OUK8RTOU.png 2R9RJ]4(3DD(B@@OUK8RTOU.png](http://files.chinaaet.com/images/2017/05/02/6362935518540463105017854.png)
由基函数的定义可知,式(4)定义的曲线实际上含有4个形状参数μi、λi+1、μi-1、λi,利用这些参数可以达到整体及局部可调,以下分两种情况讨论:
(1)当μi=λi=μi-1=λi+1=μ时,即为单参数曲线,αi、βi与形状参数无关,μ增大时,曲线越靠近线段Pi-2Pi-1,μ起整体调控的作用。图4的曲线从上到下μ=1、0.5、0。
(2)当λi≠μi-1且μi≠λi+1时,这时αi、βi与形状参数有关,当λi=-1,μi=-1 时曲线段为直线段Pi-3Pi。图5中,曲线2的μ1=-0.5,λ2=0.8,μ3=-1,λ4=0.2,可见曲线右端变而左端不变;曲线3的μ1=1,λ2=-1,μ3=1,λ4=0.5,曲线左端变而右端不变;曲线1参数取μ1=0.5,λ2=λ4=0.8,μ3=-1,可见多参数比单参数更具灵活可调控性。

4椭圆及整圆的表示
定理3如果给定4个控制顶点Pi-3(-a,-b),Pi-2(-a,b),Pi-1(a,b),Pi(a,-b),其中a、b是均不为0的实数,节点等距,且令λi=μi=0,当u∈[ui,ui+1]时,ri(u) 为一段椭圆弧。
证明: 根据式(4)
ri(u)=βi4(1-costi)Pi-3+[12-αi4(1-sinti)]pi-2+
[12-βi4(1-costi)]pi-1+αi4(1-sinti)pi
经计算,有
![7S552L5~]A(7Z8]JY]W[_K4.png 7S552L5~]A(7Z8]JY]W[_K4.png](http://files.chinaaet.com/images/2017/05/02/6362935519552960476929739.png)
这即为椭圆的四分之一参数方程。
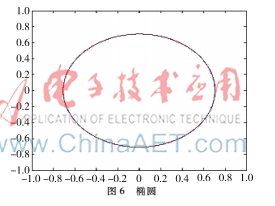
推论1对于二次三角B样条曲线,如果控制顶点为P0(-a,-b),P1(-a,b),P2(a,-b),P3(a,-b),P4(-a,-b),P5(-a,b),P6(a,b),则ri(u) 为一段椭圆。若a=b,则为整圆。图6为椭圆。
5实例应用
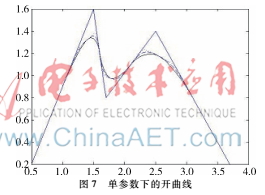
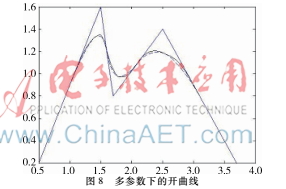
开区间和闭曲线的构造是曲线设计中的基本内容,为保证生成开的二次三角B样条曲线,只要令p0=2p1-p2,pn+1=2pn-pn-1 ,可构造插值于p1和pn且在u1和un处分别以p2-p1和pn-pn-1为切向量的开三角B样条曲线。图7表示单形状参数,λi=μi=0,0.5;图8表示多形状参数,实线对应λi=(0.4,0,0,0,-0.5,0,0.8),i=2,3,...,8,μi=(0.5,0.8,0,2,0.4,0.5,-0.2,0),i=1,2,...,7。
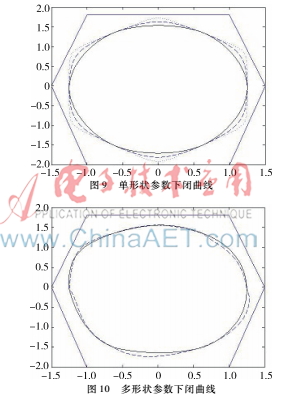
为了生成闭的二次三角B样条曲线,可增设控制点pn+1+j=pj(j=0,1,2)。令节点步长Δun+1+j=Δuj(j=0,1,2,3),及形状参数λn+1+j=λj,μn+1+j=μj,(j=0,1,2,3),于是闭曲线的表达式可写成r(u)=∑n+3i=0bi(u)pi,u∈[u3,un+3]。图9表示单形状参数下的闭曲线,λ=μ=0、0.5、1,其中实线为单形状参数λ=μ=0;图10表示多形状参数下的闭曲线,其中实线中的λi,μi与图8一样。
6结论
本文给出了在非均匀节点情形下多参数的一类二阶三角B-样条曲线,该曲线是基于四点分段,即曲线每一段只与4个控制点有关。同时它也具有二次B样条曲线的许多重要性质,如连续性、凸包性、几何不变性等。并且通过参数的取值不同可以达到整体或局部形状调控,应用重节点的技巧可以生成以此类基函数构造的开曲线和闭曲线。此外,它还可以表示椭圆及圆等圆锥曲线。
参考文献
[1] 李成刚,冯静,凌玲.基于WPF交互式绘图系统的开发[J].微型机与应用,2011,30(6):50-52.
[2] SCHOENBERG I J. On trigonometric spline interpolation[J].J.Math.M.,1964,13(5):795-825.
[3] Han Xuli. Piecewise quadratic trigonometric polynomial curves[J].Mathematics of Computation, 2003,72(243):1369-1377.
[4] Han Xuli. Cubic trigonometric polynomial curves with a shape parameter[J].Computer Aided Geometric Design,2004,21(6):535-548.
[5] 吴晓勤,韩旭里.带参数的二次三角多项式样条曲线[J].工程图学学报,2006,27(1):93-97.
[6] 王文涛,汪国昭.带形状参数的三角多项式均匀B样条[J].计算机学报,2005,28(7):1192-1198.
[7] 谢进,邬弘毅,邓四清,等.多形状参数的二次非均匀三角多项式曲线[J].工程图学报,2007,28(5):291-295.
[8] 王晶昕,王迪.均匀结点情形下的两类二阶三角B样条曲线[J].辽宁师范大学学报:自然科学版,2014,37(3):297-303.

