陈凯1,王金全1,严鋆1,蔡杰轩2,周思宇2
(1.解放军理工大学,江苏 南京 210007;2.沈阳工业大学,辽宁 沈阳 110870)
摘要:通过搭建串联故障电弧实验平台,进行多种类型负载实验,对其正常工作和发生串联电弧故障时的电流信号进行分析,提出了一种基于分形盒维数的串联故障电弧诊断方法。进一步研究了不同信噪比下分形盒维数的计算误差,分析了分形盒维数的抗噪性能,同时计算了不同负载在正常工作和发生串联电弧故障下分形盒维数的参考区间。实验证明,基于分形盒维数的故障诊断方法能够准确辨别出负载的串联电弧故障,具有较好的通用性。
关键词:串联电弧故障;故障电弧电流;分形盒维数;抗噪性能
中图分类号:TM501文献标识码:ADOI: 10.19358/j.issn.1674-7720.2017.07.022
引用格式:陈凯,王金全,严鋆,等.基于分形盒维数串联电弧故障诊断技术研究[J].微型机与应用,2017,36(7):74-77,87.
0引言
随着社会的发展,电气化程度不断提高,电气故障引发的火灾事故越来越频繁,电气火灾已成为火灾事故最重要的一部分[1]。根据我国消防局提供的相关数据表明,全国每年约有31%的电气火灾是由电弧故障所引起的[2]。
当线路中发生电弧故障时,电弧附近的物理特征值较明显,比如温度、弧压、弧光、弧声、电磁波等特征信号[3-4],但这些特征均在电弧发生点附近,局限性较大。近年来通过采集电路中的相关电流、电压信号进行故障电弧检测取得了一定的进展。文献[5]提出了利用分形盒维数和支持向量机相结合的方法进行串联电弧的辨识,但文中对于盒维数的计算方法“选取线性度较好的区域”受人为因素影响,难以机器实现,并且没有考虑噪声信号对于盒维数计算的干扰;文献[6]提出了利用自回归参数模型的辨识方法,已取得一定的效果,但该方法适用于一些特定的负载,针对其余典型负载,其判别准确率有待完善。
本文提出一种基于分形盒维数的故障电弧检测方法,该方法具有一般适用性。盒维数计算易受噪声信号的干扰,通过计算信号的盒维数发现,随着信噪比的变化,其盒维数满足一定的规律:当信噪比大于一定值时,盒维数计算值误差小,能够体现信号的分形特征,此时提取的故障电弧信号可以不加或者加以简单滤波算法就能较为准确地辨识出故障电弧信号,提高了诊断的实时性。本文依据相关标准搭建了串联故障电弧的实验平台,进行了多组各种类型负载的实验,利用本文提出的分形盒维数计算方法给出了不同负载下发生串联电弧故障时的盒维数的参考区间,从而能够实现串联故障电弧的诊断。
1分形理论
非线性负载使得传统基于傅里叶变换进行故障电弧诊断的方法失效。而分形理论能够对非线性系统中不规则的几何构型进行有效的描述,近年来,也逐渐运用到信号处理之中[7]。
1.1分形理论与分形盒维数
分形学通过事物的混乱现象与不规则的构型,将其背后的局部与整体的联系和运动规律加以描述,其中无标度性和自相似性是分形的两个最基本的特征[8]。在分形理论中,分形维数能够很好地描绘出系统的非线性度和混沌吸引子的复杂程度[9]。常见的分形维数有盒维数、关联维数、Lyapunov维数、Hausdroff维数等。其中盒维数方便数学计算和实验测量,需要设置的参数少,在实际中运用较多。
1.2分形盒维数的计算方法
设M为Rn中任一非空有界子集,记N(M,δ)表示最大直径为δ且能够覆盖M集合的最小数,则M的盒维数定义为:
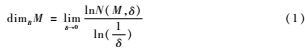
对于离散信号y(i)Y(Y是n维欧式空间Rn上的闭集),无法利用定义求极限,本文将数字离散化的信号空间点集盒维数的计算方法进行如下简化:
设信号的采样序列为y(1), y(2), y(3) ,… , y(N), y(N+1),其中N为偶数,令:

且N(ε)=F(ε)/ε, N(2ε)=F(2ε)/2ε,其中样本间隔ε=1/fs,fs为样本信号的采样频率,那么离散信号的盒维数为:
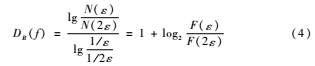
盒维数的计算值易受到噪声信号的干扰,为消除干扰,通常采用滤波算法,但这也相应地提高了信号处理的难度,在实际运用中会降低故障诊断的实时性。本文针对噪声信号对分形盒维数计算的影响进行分析,发现分形盒维数具有一定的抗噪性能,在合理的范围内,无需滤波算法也能够提高信号的处理速度。
1.3基于分形盒维数的故障电弧诊断方法
分别对负载处于正常工作和发生串联电弧故障时采集到的线路中的电流信号利用式(2)~(4)进行计算,得到两个不同的分形盒维数值,进行多组实验,可获得负载正常工作与发生电弧故障时分形盒维数的参考区间。对采集的电流信号利用分形盒维数进行判断,可以作为故障诊断的依据。下文进一步进行实验数据验证。
2串联电弧实验平台的搭建以及模型仿真
2.1串联电弧实验平台的建立
电弧的伏安特性是交流电弧最重要的物理特性之一。参照美国UL1699—2011《电弧故障断路器安全标准》进行串联电弧模拟实验平台的搭建。如图1所示,实验平台包括了各种类型的负载、电弧发生器、高精度电流传感器、Tektronix MDO3054示波器等。

其中负载包括白炽灯、电风扇、计算机、荧光灯等。电弧发生器根据上述标准自行制作安装。通过实验采集不同负载在正常工作和发生串联电弧故障时的电流数据以作后续研究。
2.2典型负载故障电弧信号分析
典型负载类型包括了常规线性负载和非线性负载,这些负载的工作波形各不相同,其故障电弧信号也有着不同的故障特征,以白炽灯(线性负载)和计算机(非线性负载)为例,分析其正常工作时以及故障电弧工作时的波形特征。

图2为白炽灯正常工作和发生串联电弧故障时的电流波形。从图中可以看出,白炽灯正常工作时其电流波形接近于标准正弦波,而故障电弧波形发生较严重的畸变。分析其故障电弧波形频谱图发现含有大量谐波,以此可以作为纯阻性负载的故障电弧判据。
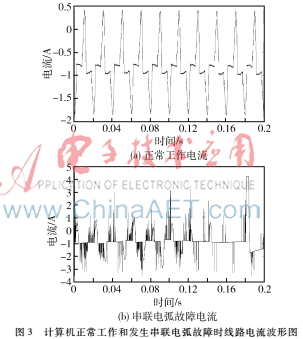
图3为计算机负载正常工作和发生串联电弧故障时的电流波形。从图中可以看出,非线性负载在正常工作时电流畸变就非常严重,出现了类似于纯阻性负载发生故障电弧故障时的“零休”现象,而发生电弧故障时,电流畸变更加严重,傅里叶变换求谐波进行故障判别的方法失效。
2.3交流电弧模型的仿真分析
目前电弧模型主要有三种:黑箱模型、数学模型以及其他一些解析和图解工具。其中基于能量角度比较经典的数学模型为Cassie模型和Mayr模型[10],但是这两种模型并不能反映出交流电弧的外特性。本文采用Tammy Gammon和John Matthews[11]提出的受控源数学模型(如式(5)所示),该模型能够较好地吻合线性负载下交流串联电弧的电流电压特性。下文以该模型为基础研究分形盒维数抗噪性能。
![Y][E$_7}]0%4Z9NE56L`JRL.png Y][E$_7}]0%4Z9NE56L`JRL.png](http://files.chinaaet.com/images/2017/05/03/6362944383129614383155790.png)
式中,Vmax为电源电压,iarc为线路中电流,L为线路中电感,R为线路中阻抗,g为固定值,一般取0.02。根据模型仿真出故障电弧波形如图4所示。

3.1高斯白噪声信号和含噪故障电弧信号的盒维数分析
噪声信号与故障信号有着其固有的分形特征,因此盒维数值也固定。通常采集的信号中含有高斯白噪声,其功率密度谱为常数,幅度分布服从高斯分布。为获取信号盒维数随着信噪比的变化规律,设置不同信噪比值,求得故障电弧信号在不同噪声强度下盒维数值,如图5所示。

对信噪比小于34的区间进行4次多项式曲线拟合可得:
y=2×10-7x4-7×10-6x3-1.1×10-4x2-6.2×10-4x+1.4(6)
式中,y为盒维数计算值,x为信噪比值(x<34),计算得到残差模为0.075 1。
3.2分形盒维数抗噪性分析
众所周知,分形盒维数的数值容易受到噪声信号的干扰。根据以上分析,将计算的盒维数误差小于1%的对应信噪比值称为C值。对于线性负载串联故障电弧信号,C值为34。当信噪比>C时,计算的分形盒维数值稳定,误差小,能够反映出信号的分形特征;当信噪比<C时,此时分形盒维数的计算值随着信噪比变化满足多项式曲线函数。
根据式(1),盒维数的两个重要标度,一个是超立方体的边长δ,另一个是用来填充M空间的超立方体的个数N(M,δ)。从空间几何的角度考虑,分形维数反映了信号对系统的填充能力和信号的复杂程度。在原信号叠加了噪声信号时,当信噪比较大,原信号占主导地位,信号空间分形特征与原信号类似;而当信噪比较小时,信号空间已被噪声信号干扰,超立方体的填充数受噪声信号的影响,此时计算的盒维数是不准确的。从本节分析可以看出,盒维数对于噪声具有一定抵抗特性,在信噪比较大时,无需复杂滤波算法,提高了故障信号诊断的快速性。然后进行盒维数计算,此时计算的盒维数能够较为准确地反应出故障信号的分形特征,从而对线路中的故障电弧信号进行准确判别[8]。
4基于分形盒维数的电弧故障诊断方法的实验验证
根据搭建的串联电弧故障实验平台进行带各种典型负载的实验。实验中负载有两种工作状态:正常工作和发生串联电弧故障。进行故障电弧实验时,由于空气的击穿电压较大,因此,需要不断调试铜棒与碳棒之间的距离,以达成空气击穿。每组负载采集80组数据,其中50组作为训练集,30组作为测试集。利用公式计算不同负载在正常工作和发生串联电弧故障情况下的盒维数参考区间。如表1所示。

经计算,基于分形盒维数的电弧故障诊断方法准确率为94.67%,具有较好的诊断效果。从表1中可以看出,不同的负载其正常工作和发生串联电弧故障时盒维数有着不同的区间。本文针对单一负载进行了实验,当线路中有多种负载时,其正常工作和发生电弧故障情况下的盒维数也有着其固有区间,进行多组实验即可获得其盒维数的参考区间。
5结论
串联电弧故障是导致电气火灾故障的重要因素之一。为准确地对故障电弧信号进行辨识,本文运用了分形盒维数的方法提取了正常工作与发生故障电弧情况下的分形特征。通过搭建故障电弧实验平台进行不同的负载实验,采集了正常工作和发生串联电弧故障时的数据,同时通过仿真将信号与噪声信号进行叠加,设置了不同信噪比,分析其分形盒维数的特征。主要结论如下:
(1)线路发生串联电弧故障时线路电流发生严重畸变,产生大量谐波分量,传统以傅里叶分析的电弧故障诊断方法失效。
(2)分形盒维数具有一定的抗噪能力,信噪比较大时,无需复杂的滤波算法,能够缩短故障信号诊断的时间,提高了实时性。
(3)通过分形盒维数计算的方法能够辨别出不同负载的正常工作状态与发生串联电弧故障状态,并给出了几种典型负载在正常工作和发生串联电弧故障时分形盒维数的参考区间,同时,若线路中带有多种负载,分形盒维数的方法仍可适用,该方法有较好的适用性。
参考文献
[1] 林章.故障电弧检测的关键技术研究及断路器开发[D].杭州:中国计量学院,2013.
[2] 李世雄.中国火灾统计年鉴[M].北京:中国人事出版社,2009.
[3] GREGORY G D, KON W, DVORAK R F. More about arcfault circuit interrupters[C]. The 38th IAS Annual Meeting, Industry Applications Conference, 2003:1306-1313.
[4] 王静红, 刘教民.基于双目立视技术的开关电弧图像处理[J].电工技术学报, 2011, 26(1): 86-91.
[5] 杨凯,张认成,杨建红,等.基于分形维数和支持向量机的串联电弧故障诊断方法[J].电工技术学报,2016,31(2):70-76.
[6] 雍静,桂小智,牛亮亮,等.基于自回归参数模型的低压系统串联电弧故障识别[J].电工技术学报,2011, 26(8):213-219.
[7] 贾丽会,张修如.分形理论在信号处理中的应用[J].计算机技术与发展,2007,17(9):203-208.
[8] 郝研,王太勇,万剑,等.分形盒维数抗噪研究及其在故障诊断中的应用[J].仪器仪表学报,2011,32(3):540-544.
[9]夏晶晶,朱灏东. 基于特征辨别能力和分形维数的特征选择方法[J].微型机与应用,2010,29(7):68-71.

