0 引言

    高速自动机是小口径火炮的核心组成部件^[1]，其结构日趋精细复杂。自动机是一个复杂的动力学系统，它在火药燃烧过程中实现动能转移和能量的储存^[2]。在实弹击发时，除有较强的噪声影响外，自动机各个机构之间还会产生碰撞，碰撞产生的振动信号会在自动机表面相互影响、相互干扰，这使目前现有的故障诊断方法难以进行检测。

    EEMD^[3]算法是在经验模态分解(EMD)的基础上提出的改进算法，由于在解决模态混叠方面效果明显，所以一经提出就得到广大学者的青睐，并被广泛应用到各个领域中^[4-5]。EEMD是在采集的故障信号中加入白噪声，明确分离各个时间尺度，有效弥补了EMD引起的模态混迭现象造成的不足。 

    分形理论^[6]方法应用在故障诊断领域是近几年研究的热点，其特点是能够从整体到局部将故障量化，用分形的方法进行故障诊断时，通常通过计算分形维数来提取特征参数。应用矩阵式分形的方法对提取到的故障信号进行分形特征量化判断，从而进一步分析自动机的运行状况。

    本文提出将EEMD和矩阵分形结合的方法应用到自动机故障诊断当中，即将自动机振动信号经过EEMD分解得到分量信号，计算其广义维数；通过广义维数相关系数判断方法选取分量信号，进而构建样本矩阵；用相关性判断方法计算待检测信号矩阵与样本矩阵之间的相关系数，最后通过对比相关系数的大小来判断故障模式。诊断结果表明，本文的方法可以有效地区分故障。

1 EEMD算法

    由于EMD对信号分解出来的IMF分量常伴有模态混叠的现象，因此本文应用聚合经验模态分解，在测试信号中加入辅助信号白噪声序列，之后对多次分解的IMF分量进行总体平均来抵消加入的白噪声序列，降低模态混叠现象造成的影响。EEMD基本算法分为以下3步^[7]：

    (1)在原始振动信号x(t)中多次加入幅值具有均值为零、标准差是常数的高斯白噪声n_i(t)，即：

式中：n_i(t)为第i次加入的白噪声信号。

    (2)对x_i(t)分别进行EMD分解，得到的IMF分量c_ij(t)与1个余项r_i(t)。其中c_ij(t)为第i次加入白噪声后，经过分解所得到的第j个IMF分量。

    (3)循环步骤(1)与步骤(2)各N次，运用不相关随机序列统计均值为零的原理把上述对应的分量进行总体平均运算，去除多次加入白噪声后，对真实的IMF的影响，最终得到EEMD分解后的IMF为：

2 分形理论

2.1 广义维数

    用广义分形维数D_q来表示多重分形的分形维数，采用覆盖法计算多重分形。在实际应用中，通常用频率代替概率：

式中：分母为全部超立方体覆盖的点数；d_i为第i个超立方体覆盖的点数；N为超立方体总数。

    覆盖法利用尺度为η的大小一致的超立方体对整个对象覆盖，所需的立方体总数为N。假设落入第i个立方体的概率是p_i(l)，如果给定参数q时，其广义信息熵：

2.2 分形矩阵的构建

    由分解信号广义维数组成的分形矩阵，列向量表示同一测度下的广义分形维数，行向量表示一个分量信号的广义维数，这样即实现了把多重分形扩展为矩阵分形，则待检测的设备工况就具有了三维立体结构^[9]。

    若自动机有n种故障状态，则共有n+1种状态，采集各工况下的自动机振动信号，计算各工况下的广义维数和分形矩阵。第j种工况下，信号的分形矩阵为m×n阶的E^j，作为此工况下的样本矩阵，其中m表示分解得到的IMF信号的数量。两个分形矩阵的相关系数计算公式为：

    该函数表示了第x种待检信号与第j种工况的相关程度。R(j，x)越大，表明第x种待检信号与第j种工况相关程度越强，即说明其状态越相似，反之两者相关度就弱，进而实现故障的识别与分类。

3 自动机故障诊断实例分析

3.1 自动机故障实验设置

    本文以某型高射机枪自动机为研究对象，根据靶场工作人员的经验，本次试验采用了电火花线切割的方法，分别在自动机闭锁片和枪击框上设置裂纹槽，使裂纹在射击过程中来产生裂纹及设置故障。根据对故障的分析，结合高射机枪的实际应用，故障设置如下：(1)在闭锁片上闭锁斜面圆角处，沿半径方向设置深为1.5 mm的裂纹槽，左右两片对称，称为故障一；(2)在开锁时闭锁片回转，且垂直于闭锁片平面方向上设置1.5 mm深的裂纹槽，左右两片对称，称为故障二；(3)在机头左右两侧圆角矩形窗后端的两对圆角处，沿圆角直径各成±45°切入1.5 mm深，设置机头故障，称为故障三。图1为故障一、二、三的裂纹位置图。

    采集信号时选择在机枪机匣前侧(测点1)和枪尾上方(测点2)作为测点，布置单向压电式加速度传感器。物理坐标系规定如下：沿着枪管子弹射出方向为X轴正向，枪口左向为Y向，竖直向上方向为Z向。本次实验采样频率设置为204.8 kHz。

3.2 自动机故障特征提取与识别

    LMS采集的自动机数据，有正常、故障一、故障二、故障三 4种工况，分别对其进行EEMD分解，分解9层，其中正常工况信号分解结果如图2。

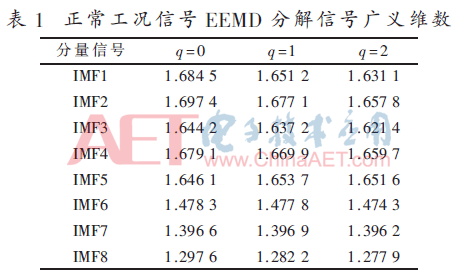
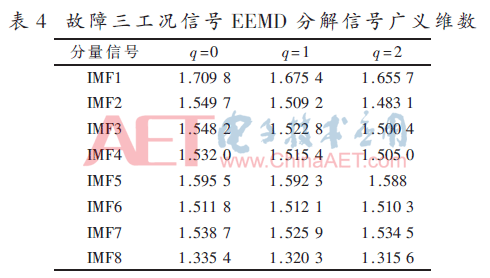
    对每种工况下通过EEMD分解得到的前8个分量信号进行广义维数计算，分别取权重因子q=0、1、2，广义维数列表如表1～表4所示。

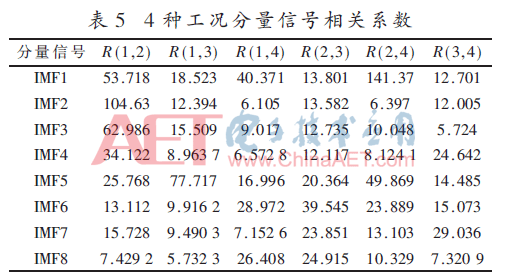
    对自动机4种工况信号，计算不同工况下对应位置上分量信号广义维数组成矩阵之间的相关系数，结果如表5所示。对相应的分量信号的相关系数求和，如表6所示。

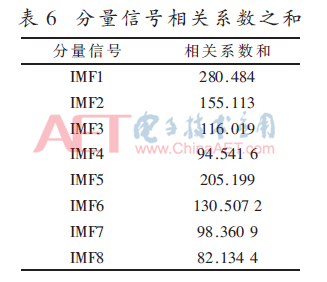
    采用相关性选择方法对信号进行选择，对各工况下分量信号相关系数总和较小的，区分能力越强，且相关系数分布较均匀的，也表明其相关性大，距离越近。根据这两种准则，选择IMF4、IMF7、IMF8这3个分量信号构建样本矩阵，分别为：

    为验证方法的可行性，选取4种工况各3组待检测数据进行检测，对于正常、故障一、故障二、故障三这4种状态对应的待检测信号，分别用EEMD进行信号分解，计算q取不同值时的广义维数，选取IMF4、IMF7、IMF8这3个分量信号构建分形矩阵，分别计算样本矩阵与4种状态下待检测信号组成的分形矩阵间的相关系数，如表7所示。

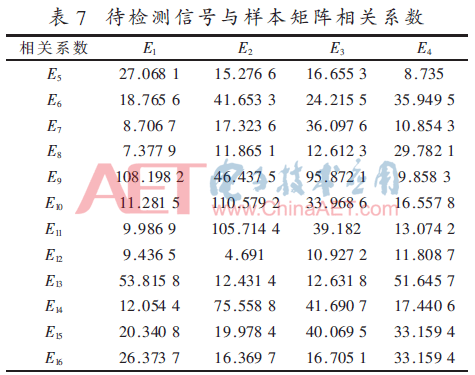
    为了直观地对诊断结果进行判断，用折线图来表示相关系数的大小，4种不同的线型分别表示待检测信号与4个样本矩阵之间的相关系数，结果如图3。

    通过对比图中相关系数的大小可以判断待检测信号的工况，对于样本矩阵E₁，待检测信号1、5、9与其相关系数最大，则它与样本矩阵E₁的工况相同，属于正常状态；同理得待检测信号2、6、7、10是故障一状态，待检测信号3、11属于故障二状态，待检测信号4、8、12是故障三状态。采用此方法与事实情况对比，发现12个待检测信号中，有11个是判断准确的，判断准确率为92%。

4 结论

    本文将分形矩阵作为特征值对自动机工况进行分析，判断结果的正确率达到92%。本文的研究验证了基于EEMD分解的矩阵分形故障诊断的实际效果。诊断结果表明，本文的方法能有效提取故障特征值并完成故障识别，解决了自动机故障诊断的问题。

参考文献

[1] 康郦，冯德朝.某中口径舰炮自动机设计思想与特点分析[J].火炮发射与控制学报，2010(2)：61-65.

[2] 成尔康，李德芬，李莉丽.自动武器学(机构力学分册)[M].北京：国防工业出版社，1994.

[3] WU Z H，HUANG N E.Ensemble empirical mode decom-position：a noise assisted data analysis method[J].Advances in Adaptive Data Analysis，2009，1(1)：1-41.

[4] 王军辉，贾嵘，谭泊.基于EEMD和模糊C均值聚类的风电机组齿轮箱故障诊断[J]．太阳能学报，2015，36(2)：319-324．

[5] 陈晓娟，车小磊，吴洁.纳米器件的散粒噪声检测方法研究[J].电子技术应用，2016，42(9)：32-35．

[6] 石博强，申焱华.机械故障诊断的分形方法-理论与实践[M].北京：冶金工业出版社，2001.

[7] Lei Yaguo，He Zhengjia，Zi Yanyang.Application of the EEMD method to rotor fault diagnosis of rotating machinery[J].Mechanical Systems and Signal Processing，2009(23)：1327-1338.

[8] 李兆飞，柴毅，李华峰.多重分形的振动信号故障特征提取方法[J].数据采集与处理，2013，28(1)：237-243.

[9] 郝研.分形维数特性分析及故障诊断分形方法研究[D].天津：天津大学，2012.

作者信息:

张玉学，潘宏侠，安  邦

（中北大学 机械与动力工程学院，山西 太原030051）