文献标识码: A
DOI:10.16157/j.issn.0258-7998.2017.04.029
中文引用格式: 王曦,张新刚. 不同耦合方式下相依网络的级联故障评估[J].电子技术应用,2017,43(4):112-116.
英文引用格式: Wang Xi,Zhang Xingang. Evaluation of cascading failure of interdependent network under several coupling preferences[J].Application of Electronic Technique,2017,43(4):112-116.
0 引言
现实中的社会经济网络与各种电力、通信、水电等基础设施网络存在逻辑和功能上的依赖,一个网络的运行依赖于另一个或几个网络的运行,比如电力网络正常运行为通信网络提供电力保障,通信网络正常运行又给电力网络提供调控信息,彼此形成更复杂的电力-通信网络。这种由若干网络彼此依赖而耦合成的网络称为“相依网络”。
相依网络的正常运行至关重要,相应的故障研究工作起源于文献[1],BULDYREV S V在文献[1]中研究了一对一互连的全相依网络模型,得出相依网络的故障渗流过程为一阶形式,即网络节点比例移除达到一定阈值,网络完整性会急剧下降,这一结论有别于单一或孤立网络,单一或孤立网络移除节点时的表现形式是逐步下降的二阶形式。文献[2]对相依网络采用负载局部分配原则的容量-负载模型,分析子网络间的耦合强度、子网络类型和耦合边的故障影响。文献[3]研究不同攻击策略对相依网络的影响,发现同时考虑不同子网节点度的攻击策略比考虑单一子网的攻击策略更有效、破坏更严重。文献[4]介绍相依网络的来龙去脉,并以经济网络的相依网络为例,得出不同经济因素的排名,表明中国经济增长趋势强劲。文献[5]在相依网络的故障中综合考虑相依边的依赖关系、负载作用,提出一种相依网络模型,同时还提出一种主动的、但存在微弱扰动的故障恢复策略。文献[6]提出一种节点外部度和内部度可调关系的相依网络负载-容量模型,以研究外部度和内部度等因素对级联故障的影响。文献[7]构建双层相依控制网络模型,发现子网的平均度越大,网络越鲁棒。文献[8]提出网络间同地位节点耦合的相依网络构建方法,将随机网络和无标度网络作为耦合的子网,模拟故障渗流由一阶非连续相变到二阶连续相变的过程。文献[9]提出一种考虑负载作用的级联故障模型和低成本的故障抑制策略。
上述研究现状存在几点不足:(1)负载分配策略采用局部分配策略,而实际中的节点故障会导致网络负载发生全局重分配;(2)评估指标局限于最大连通子图,故障评估不够全面。本文基于节点负载全局重分配策略,对相依边为逻辑依赖的相依网络仿真分析,采用(非)最大连通子图占比、迭代步长和首次迭代中(平均/最大)最短路径长度等指标对相依网络进行较全面的评估。
1 相依网络模型
1.1 相依网络简述
单个或孤立的子网之间通过物理依附、逻辑依赖等方式耦合成相依网络。连接不同子网节点的边称作相依边,物理依附是指相依边两侧的不同子网节点存在功能依赖:相依边一侧节点故障,另一侧节点也同样会故障。逻辑依赖是指相依边两侧不同子网节点存在结构上的逻辑依赖:相依边一侧节点故障不一定会导致另一侧节点故障。
节点度指节点的邻居节点数目,度越大,节点邻居节点越多。不同子网的节点一对一互连耦合时,存在3种耦合方式:随机耦合、同配耦合和异配耦合。随机耦合指一子网中节点随机选择另一子网中节点连接。同配耦合指一子网中大度节点与另一子网中大度节点连接,而小度节点与另一子网中小度节点连接。异配耦合指一子网中大度节点与另一子网中小度节点连接[10]。
子网中参与连边耦合的节点占比代表耦合强度,节点占比越大说明耦合强度越大,若两个子网的全部节点参与耦合互连,则称为全相依网络,否则称为部分相依网络。
1.2 相依网络模型构建过程
将某个独立的子网记作子网1,对子网1复制一份副本,记作子网2。按照以下2步构建全相依网络:
(1)依据不同节点度(即节点的邻居节点数目)排序规则,对子网1和子网2中节点排序,见表1。

(2)按照表1,对子网1和子网2中全部节点自上而下一对一依次互连。
通过以上步骤,生成随机耦合全相依网络、同配耦合全相依网络和异配耦合全相依网络,在不引起歧义的前提下,分别简称:随机网络、同配网络和异配网络。图1是随机耦合的全相依网络的示意图。
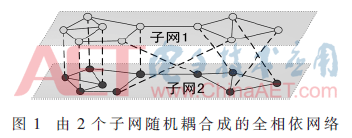
图1是由子网1和子网2节点一对一随机互连的全相依网络。实线代表子网内的连边,称之为“连接边”,虚线代表子网间的“相依边”。
2 负载全局重分配的级联故障模型
通信、电力等网络,其信息等物理量在网络节点对之间传递,每个节点有一定初始负载和容量以维持网络功能。

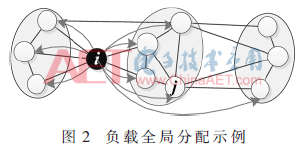
3 相依网络的性质
仿真所用子网数据为电网拓扑IEEE118网络和新英格兰高压电England网络,分别为118个节点和120个节点。依据前文的相依网络模型,形成IEEE118随机网络、IEEE118同配网络、IEEE118异配网络、England随机网络、England同配网络和England异配网络,拓扑性质如表2和表3所示。

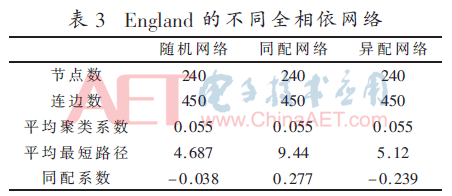
依表2和表3可知,不同耦合方式相依网络的平均聚类系数近似,随机网络和异配网络的平均最短路径比同配网络小。同配网络的同配系数为正数,而随机网络和异配网络的同配系数为负数,这与相依网络构建原理一致。
4 不同评估指标的仿真分析
采用MATLAB仿真级联故障,初始故障节点选择子网1中节点,相依边为逻辑依赖。子网2节点只会由于过载而故障,不会由于相依边的依赖而故障。采用多个指标评估级联故障对相依网络的影响,仿真结果为子网1中全部节点迭代20次的平均值。
4.1 最大连通子图分析
4.1.1 最大连通子图占比
由于相依网络中不同子网部分节点之间存在逻辑依赖,所以限定评估指标—最大连通子图必需同时包含2个子网的节点,否则说明网络已完全崩溃。
最大连通子图占比表征为故障后剩余节点中最大连通子图节点数目在节点总数中的占比,占比越大,级联故障对相依网络的破坏作用越小,结果如图3所示。

分析可知,容忍系数β越大,最大连通子图占比越大,级联故障的破坏作用越小。IEEE118和England的随机网络和异配网络在不同β下的级联故障结果类似。在β=0时,同配网络对应的最大连通子图占比偏大,级联故障破坏最小;而0.1≤β≤0.8时,同配网络对应的最大连通子图占比偏小,级联故障对同配相依网络的破坏最大。
4.1.2 非最大连通子图占比
在每一迭代步后,通过计算不属于最大连通子图的节点数目与节点总数的比值,结果如图4所示。

总体趋势而言,β越大,非最大连通子图占比越小,这是由于β越大,网络越冗余,级联故障对网络的破坏越小,不属于最大连通子图的节点越少。同时,在β值一定时,随机网络和异配网络的结果类似,而同配网络对应的y值明显大于随机网络和异配网络,即在遭受级联故障后,同配网络受到更大程度的破坏。
4.2 迭代步长分析
迭代步长描述从初始故障节点开始,级联故障一层一层扩散的现象,代表网络达到稳态时的故障迭代次数。迭代步长越大,网络达到稳定时间越晚,级联故障的影响越久;步长越小,网络达到稳态时间越早,级联故障的影响越短,结果如图5所示。
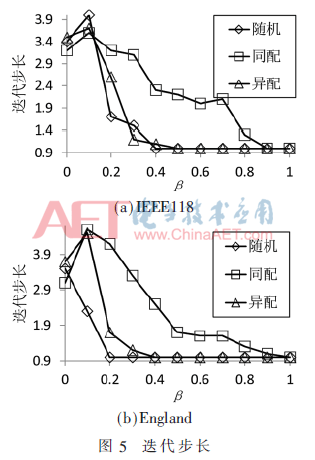
由图可知,迭代步长总体趋势为随着β变化,先增加至峰值再递减。β=0.1时,迭代步长达到峰值,β>0.1,迭代步长随着网络冗余的增大而减少,且同配网络的迭代步长下降最为缓慢,网络达到稳定越晚。IEEE118同配网络在β≤0.1时,达到稳定更早。England不同相依网络在β≥0.1时,迭代步长差异显著。
4.3 首次迭代步中最短路径长度分析
4.3.1 首次迭代步中过载节点的平均最短路径长度
初始故障节点i,定义f(n)为第n个迭代步中过载节点集合,|f(n)|代表相应的节点数目,k∈f(n),则:

其中,dst(1)为首次故障迭代步中过载节点的平均最短路径长度。由于在n≥2时,不同迭代步之间存在多个故障触发源,不便于分析,这里取n=1。图6是相依网络首次迭代步中过载节点的平均最短路径长度。
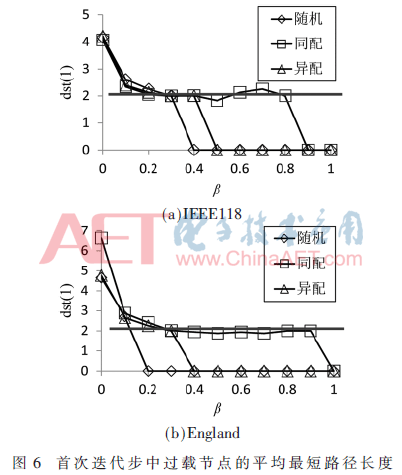
由图6可知,β∈(0,0.2)时,β越大,dst(1)越小,说明网络越冗余,过载节点越倾向分布在初始故障节点附近。对比随机网络和异配网络,同配网络在β≥0.3时,dst(1)略有波动但总体不变,说明网络冗余超过一定阈值,过载节点与初始故障节点具备相对不变距离(≈2),即故障节点邻居节点的邻居节点。随机网络和异配网络的dst(1)在更小的β下达到0,这是因为随机网络和异配网络在此β下已达到稳态。在β=0(即网络无冗余)时,England同配网络的过载节点倾向分布在远离初始故障节点处,而IEEE118不同相依网络则无区别。
4.3.2 首次迭代步中过载节点的最大最短路径长度
定义fmax(n)为第n次迭代步中,距离初始故障节点i最远的过载节点,则:

其中,dstmax(1)代表首次迭代步中过载节点的最大最短路径长度,结果如图7所示。

从图7可知,dstmax(1)曲线下降趋势先快后缓慢。当β=0时,过载节点非常远离初始故障节点;β=0.1时,dstmax(1)明显小于β=0时值,说明较小的网络冗余能显著降低最远的过载节点距离;继续增大网络冗余(β≥0.2),则对降低过载节点最远距离无显著作用(≈2、3)。IEEE118和England同配网络在β∈(0,0.4)下的dstmax(1)值明显区别于随机网络和异配网络。
5 结论
本文对IEEE118电网和England网络作为子网进行耦合,依据不同耦合方式,构建3种不同的相依网络。通过对不同相依网络仿真级联故障,并从最大连通子图、迭代步长和过载节点分布对级联故障深入分析,发现同配网络比异配网络和随机网络更脆弱,级联故障对同配网络的破坏更持久,而随机网络和异配网络具备相似的级联故障特性。通过本文研究可知,现实网络耦合时应避免同配方式耦合,在故障发生前(后)时,应有针对性地预防(检修)故障节点的邻居节点的邻居节点,避免盲目工作。
参考文献
[1] BULDYREV S V,PARSHANI R,PAUL G,et al.Catastrophic cascade of failures in interdependent networks[C].APS March Meeting 2010.American Physical Society,2010:1025.
[2] 陈世明,邹小群,吕辉,等.面向级联失效的相依网络鲁棒性研究[J].物理学报,2014,63(2):428-437.
[3] 刘润然,贾春晓,章剑林,等.相依网络在不同攻击策略下的鲁棒性[J].上海理工大学学报,2012(3):235-239.
[4] HAVLIN S,KENETT D Y.Cascading failures in interdependent economic networks[C].Proceedings of the International Conference on Social Modeling and Simulation,plus Econo-physics Colloquium 2014.Springer International Publishing,2015.
[5] Hong Sheng,Lv Chuan,Zhao Tingdi,et al.Cascading failure analysis and restoration strategy in an interdependent network[J].Journal of Physics A Mathematical General,2016,49(19):195101.
[6] 彭兴钊,姚宏,杜军,等.负荷作用下相依网络中的级联故障[J].物理学报,2015,64(4):351-358.
[7] 韩海艳,杨任农,李浩亮,等.双层相依指挥控制网络级联失效研究[J].中南大学学报:自然科学版,2015(12):4542-4547.
[8] 李稳国,邓曙光,杨冰,等.相互依存网络间的拓扑构建方法[J].计算机工程与应用,2014(11):85-89.
[9] HONG S,WANG B,MA X,et al.Failure cascade in interdependent network with traffic loads[J].Journal of Physics A Mathematical & Theoretical,2015,48(48):485101.
[10] 刘漳辉,陈国龙,汤振立,等.加权复杂网络相继故障的节点动态模型研究[J].小型微型计算机系统,2013,34(12):2800-2804.
[11] Lin Guoqiang,Di Zengru,Fan Ying.Cascading failures in complex networks with community structure[J].International Journal of Modern Physics C,2014,25(5):323-337.
作者信息:
王 曦,张新刚
(南阳师范学院 软件学院,河南 南阳473061)

