李胜男1,2,李永贵2,闫岩1
(1. 解放军理工大学 通信工程学院,江苏 南京 210007;2. 南京电讯技术研究所,江苏 南京 210007) 摘要:现有的跳频序列,由于综合性能不均衡,参数无法实时改变,无法直接应用于动态频谱抗干扰系统中,因此迫切需要研究一种适用于动态频谱抗干扰系统的动态跳频序列。基于m伪随机序列,提出了一种频率数可根据通信环境实时变化的跳频序列。仿真结果表明,与基于固定参数的频率自适应跳频序列相比,动态跳频序列在均匀性、随机性、汉明相关性等方面均具有更好的性能。
关键词:动态频谱抗干扰;跳频序列;任意频率数;均匀性
中图分类号:TN914.41文献标识码:ADOI: 10.19358/j.issn.1674-7720.2017.08.022
引用格式:李胜男,李永贵,闫岩.动态频谱抗干扰系统中跳频序列研究[J].微型机与应用,2017,36(8):70-72,75.
0引言
*基金项目:国家自然科学基金(61401505);江苏省自然科学基金(BK20151450)作为跳频通信三大关键技术之一,跳频序列对跳频通信系统的性能有着决定性的影响。目前常见的跳频序列主要有基于有限域的跳频序列、基于混沌理论的跳频序列以及基于密码学的跳频序列等[14]。然而,这些跳频序列大多是针对频率数为素数的整数次幂(即pk,p为素数)的跳频系统而设计的,而实际的跳频通信难以满足可用频率数为整数幂的要求[5]。特别地,在动态频谱抗干扰系统[67]中,构成跳频频率表的频率数、频率值、分布带宽等频谱资源随着频谱感知的结果实时、动态变化,现有的跳频序列由于综合统计性能不均衡,参数无法实时改变,无法直接应用于动态频谱抗干扰系统中。因此,研究适用于动态频谱抗干扰系统的动态跳频序列技术,是实现动态频谱抗干扰系统必须要解决的问题。
文献[89]基于重新映射思想,提出了一种频率数为pk-pm的跳频序列产生方法,但其从根本上并没有跳出整数幂的思想。文献[10]基于分段映射、奇偶交替思想,提出了一种任意频率数跳频序列构造方法,该方法生成的序列具有较好的一维均匀性,但二维均匀性和随机性较差,同时频率数难以实时改变。文献[11]基于3DES算法,提出了一种任意频率数跳频序列构造方法,然而,3DES算法属于公开算法,势必还会经历长期的攻击考验[12],而且,实际跳频电台中常采用的方法是,在单个m序列发生器上加非线性前馈逻辑,或者用几个m序列发生器进行非线性组合,再通过抽头选取,从而得到高度非线性的跳频序列。
因此,本文首先基于m序列,通过抽头模型,产生多组跳频独立序列。然后,根据频谱感知得出的可用频率数等系统参数对跳频独立序列进行伪随机映射,提出一种频率数实时可变的跳频序列构造方法。仿真证明它在均匀性、随机性、汉明相关性等方面均具有良好的统计性能,同时,频率数能够为任意值,且实时改变。
1系统模型
动态频谱抗干扰系统在传统无线通信系统中引入动态频谱接入思想,在对电磁环境实时、有效感知的基础上,通过智能决策及动态调整通信参数,提高无线通信系统的电磁环境适应能力、抗干扰能力和多用户组网高效性。如图1所示,假设系统中共有N1个通信用户Uk(k=1,…,N1),N2个干扰用户Jk(k=1,…,N2)。假设每个通信周期分为四个阶段:同步阶段、频谱感知阶段、智能决策阶段和通信阶段。在时间同步阶段,系统中所有通信用户将本地的TOD调整为相同。完成时间同步后,系统进入频谱感知阶段(这一阶段一直在进行,直到通信结束),所有通信用户对频谱环境进行感知,得到分布带宽内所有可用频谱。在智能决策阶段,网控中心根据感知结果得到本周期内系统的通信参数(如频率数、跳频间隔、功率、调制方式等)以及系统所要实现的最优目标,对各通信用户的频谱分配和使用进行决策。在通信阶段,各通信用户根据决策结果完成通信。

为实现动态频谱抗干扰通信,必须设计一种能使信号在无干扰、可用信道上传输的动态跳频序列。假设第k个周期内无干扰、可用频率数为qk ,则动态跳频序列可表示为F={ft|t=1,2,3,…},其中,ft∈{1,2,…,qk}。
2动态跳频序列生成算法
基于上述假设,动态跳频序列可以根据动态参数实时生成。动态跳频序列生成原理图如图2所示。

2.1独立跳频序列的产生
首先,利用N个不同的n级本原多项式产生N条m序列。然后,选取r(本文中r取8)个非相邻级抽头,根据公式(1)产生N个独立伪随机跳频序列族S1~SN。其中,SN={sNt},t为时刻,u=u0u1…u7为地址码。
snt=128[(at+u0)mod2]+64[(at+2+u1)mod2]+
32[(at+4+u2)mod2]+16[(at+6+u3)mod2]+
8[(at+8+u4)mod2]+4[(at+10+u5)mod2]+
2[(at+12+u6)mod2]+(at+14+u7)mod2(1)
2.2序列选择
首先,由实时感知得到的频率数为qk,根据公式(2)设置门限THm:
THm=qk(2)
然后,根据公式(3),将N条跳频序列的t时刻的跳频码与门限值逐一比较,找到第一个小于门限值的跳频码,得到参数m。

2.3伪随机映射
根据公式(4),并依据k周期内可用的频率数,得到t时刻的跳频码。通过时钟驱动,从而得到所需长度的跳频序列:
![SO4$A5[_XD_FX@[PB]~YZZJ.png SO4$A5[_XD_FX@[PB]~YZZJ.png](http://files.chinaaet.com/images/2017/06/04/6363221714717406089107423.png)
3仿真及性能分析
跳频序列的综合统计性能对跳频通信系统起着决定性作用,为了验证本文提出方法产生的跳频序列的性能,本文从均匀性、随机性、汉明相关性等方面对跳频序列进行性能分析,并与工程上应用广泛的基于固定参数的频率自适应跳频序列比较分析。仿真参数如表1所示。

3.1均匀性
均匀性通常分为一维均匀性和二维均匀性。一维均匀性是指各跳频码出现的概率相等,即P(ft=i)=1/qk(i=1,…,qk)。二维均匀性是指各跳频码对连续出现的概率相等,即跳频码ft出现后紧接着出现跳频码ft的联合概率相等,P(ft=i,ft+1=j)=1/qk2。其中,i,j=1,…,qk。
序列的均匀性常用χ2检验法验证。以检验一维均匀性为例,检验假设H0={序列服从均匀分布},则检验统计量为:

其中,num(fi)表示在长度为L的序列中,跳频码ft(ft∈{1,2,…,qk})出现的次数。在假设H0下,若根据公式(5)求得的χ2值有χ2<χ21-α(qk-1),则在置信水平α下接受H0。当频率数为79时,在置信水平α=0.5的前提下,均匀性卡方检测的理论参考值为99.3。
均匀性仿真曲线如图3所示。由图3可知,基于固定参数的频率自适应跳频序列的均匀性卡方检测值明显高于理论参考值,而动态跳频序列的卡方检测值均低于理论参考值。因此,可以认为动态跳频序列具有较好的均匀性。

3.2随机性
随机性常用来表征两个随机数之间的统计相关性是否显著。序列的随机性常用列联表检验法检验。假设H0={两个序列相互独立},长度为L的跳频序列为F0={f1,…,fL},平移τ位后的序列为Fτ={f1+τ,…,fL+τ}。其中,τ=0,1,…,L-1。将两跳频序列中的跳频码按先后顺序两两分组,得到(f1,f1+τ), (f2,f2+τ),…,(fL,fL+τ)。记nij为各频率对出现的数量,ni=∑qkj=1nij,nj=∑qki=1nij,则检验统计量为:

在假设H0下,若根据公式(6)求得的值有<χ21-α((qk-1)2),则在置信水平α下接受H0。当频率数为79时,在置信水平α=0.5的前提下,随机性卡方检测的理论参考值为6 266.3。
图4随机性仿真曲线随机性仿真曲线如图4所示。由图4可知,在码子距离小于10时,基于固定参数的频率自适应跳频序列的随机性卡方检测值高于理论参考值,而动态跳频序列的卡方检测值始终低于理论参考值。因此,可以认为动态跳频序列具有较好的随机性。
3.3汉明相关性
汉明相关性分为汉明自相关和汉明互相关,它们表征了序列间的碰撞特性,反映了系统的抗衰落能力和用户间组网的碰撞情况。周期为L的两个序列在时延τ时的周期汉明相关定义为:

显然,汉明相关值越小,汉明相关性越好。
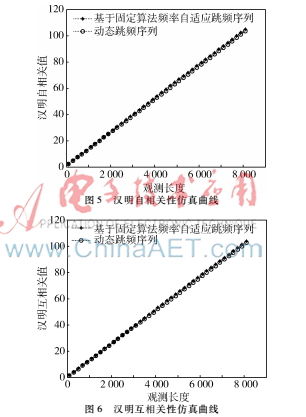
汉明自相关及互相关仿真曲线分别如图5、图6所示。由图5、图6可知,动态跳频序列的汉明自相关值和汉明互相关值都略微低于基于固定参数的频率自适应跳频序列的汉明自相关值和汉明互相关值。因此,可以认为动态跳频序列具有更好的汉明相关性。
3.4实时性
动态跳频序列与常规跳频序列的最大不同是频率数可取任意值,且能根据感知环境实时变化。因此,图7给出了频率数分别为79、180、256、200时的时频图。由图7可知,动态跳频序列具有较好的实时性。
3.5游程特性
跳频序列中取值相同的相继的(连在一起的)元素合称为一个“游程”。在一个游程中元素的个数称为游程长度,也就是在某个频率上的停留时间。为了抗截获和转发式干扰,跳频序列的最长游程越小越好。表2给出了完全随机序列的不同游程长度的理论参考值和动态跳频序列的检测值。

由表2可知,动态跳频序列的游程特性与理论参考值基本一致。因此,可以认为动态跳频序列具有较好的游程特性。

4结论
针对现有跳频序列的频率数只能为素数的整数次幂的不足,本文基于m序列,利用非连续抽头法,提出了一种频率数可为任意值的跳频序列。仿真结果表明,与基于固定参数的频率自适应跳频序列相比,本文提出的跳频序列具有较好的均匀性、随机性、汉明相关性等性能,同时,频率数可为任意值,且能根据通信环境实时变化。
参考文献
[1] 姚富强. 通信抗干扰工程与实践(第二版)[M]. 北京: 电子工业出版社, 2012.
[2] 梅文华. 跳频序列设计[M]. 北京: 国防工业出版社, 2016.
[3] 李伟, 禹思敏. 基于 Logistic 映射的混沌跳频信号发生器设计与实现[J]. 微型机与应用, 2010,29(3): 44-48.
[4] 李思奇, 全厚德, 崔佩璋, 等. 基于混沌特性的跳频序列复杂度分析[J]. 电子技术应用, 2013, 39(8): 113-116.
[5] 关磊. 高性能智能跳频序列族构建与组网理论研究[D]. 西安:西安电子科技大学, 2015.
[6] 朱毅超, 陆建勋. 动态频谱抗干扰系统在部分频带干扰下的性能[J]. 电子学报, 2011, 39(10): 2331-2337.
[7] 朱毅超, 梁亮, 田骅, 等. 一种基于认知的动态频谱抗干扰新技术[J]. 通信技术, 2014, 47(1): 72-75.
[8] PARK S B, LEE K E, CHOI Y K, et al. Some good frequency hopping sequences with arbitrary number of slots[C].Military Communications Conference, MILCOM 2001, Communications for NetworkCentric Operations: Creating the Information Force, IEEE, 2001, 2: 13251329.
[9] 李赞, 廖丽思, 金力军, 等. 适用于任意频隙数的跳频序列族产生方法研究[J]. 无线电工程, 2004, 34(4): 1-3.
[10] 耿阿囡, 黄训诚, 庄奕琪, 等. 一种任意频隙跳频序列构造方法[J]. 通信技术, 2007 (4): 5456.
[11] Guan Lei, Li Zan, Xiao Song, et al. A family of adaptive frequency slot number FH sequences for high security and reliability communication[C].Intelligence and Security Informatics Conference (EISIC), 2015 European, IEEE, 2015: 3036.
[12] 张邦宁,魏安全,郭道省. 通信抗干扰技术[M]. 北京: 机械工业出版社, 2006.

