0 引言

    对于火星着陆任务，火星探测器在EDL(Entry，Descent，Landing)阶段与地球通信非常具有挑战性。火星探测器进入火星大气后会剧烈减速，这种加速度和抖动使发送的X波段信号(8.4 GHz)产生严重的多普勒动态。1999年，美国发射的“火星极地探测器”(Mars Polar Lander，MPL)由于经费限制，没有设计EDL过程中的通信系统，任务失败后难以找到失败的根本原因^[1]。此后，美国进行的火星探测软着陆任务在EDL过程中都采用了MFSK通信方式。因此，研究火星探测器在EDL过程中的通信体制能为我国火星探测的实施提供借鉴，具有重要意义。

    火星探测器EDL过程中，利用直接对地通信链路发送一种类似于旗语的MFSK信号，通过数据音与载波之间的频率间隔来传递信息。由于通信距离极远，且多普勒动态非常大，接收信号载噪比通常在24 dB-Hz以下^[2]，进行这种极低信噪比、高动态信号检测的方法有：(1)最大似然（ML）准则估计算法：传统的最大似然估计算法是基于多维搜索的非线性优化问题，运算复杂度较高，很难进行实际应用。文献[3]针对高动态微弱信号提出了基于最大似然法的频率估计方法，该算法是最基本的最大似然估计算法，运算量庞大；文献[4]提出了基于相位加权求和、1阶2阶相位差的参数估计算法，简化了传统的最大似然估计算法；文献[5]提出了一种离散的高阶相位函数法，可用于高阶多普勒动态估计，但该方法只适用于中高信噪比时载波捕获；文献[6]提出了一种载波恢复增强的最大似然多普勒频率偏移算法，该算法通过增加数据音、数据音相位两个维度的搜索，将信号检测门限降低了3 dB，但是这种方法的运算量会扩大2 000倍，不可能进行信号实时检测；(2)含FFT处理的最大似然检测算法：文献[7-8]提出了时域匹配平均周期图算法(Time-Domain Matching-Average Periodogram algorithm，TDMAP)，这种算法减弱了多普勒变化率匹配精度要求，运算复杂度降低，适用于载波捕获。但当动态范围扩大时，匹配支路也成比例增加，运算复杂度扩大，从而给火星探测信号的载波实时捕获带来困难。文献[9-10]针对传统的时域匹配平均周期图算法计算复杂度高的问题，提出了一种改进的带有补零的频域移位平均周期图算法。该算法与原算法相比，其计算复杂度降低倍数为匹配支路数与补零倍数之比，捕获性能几乎不损失。文献[11-12]对高动态微弱信号完成频率捕获后提出了一种自适应的信号跟踪方法。

    以上研究成果主要用于对极低信噪比、高动态信号进行载波捕获/跟踪、信息检测，没有从信号体制上分析研究MFSK信号不同的调制指数对信号检测性能的影响，没有研究为什么火星科学实验室(MSL)将MFSK数据音之间的频率间隔设为76 Hz，不同的频率间隔对信号检测性能是否有影响。另外，多普勒频率变化率的大小对信号检测性能的影响也未进行定量分析。

    本文分析了MER、Phoenix、MSL在火星EDL过程中直接对地通信使用的MFSK信号及文献[7-8]中用于MFSK信号检测的时域匹配平均周期图算法，通过仿真火星科学实验室EDL过程中的多普勒动态，研究了MFSK调制指数、数据音频率间隔以及捕获/跟踪阶段多普勒频率变化率的大小对信息解算性能的影响，并根据研究成果提出以下建议：将数据音频率间隔设为80 Hz，当载噪比噪比低于17 dB-Hz时，调制指数应设为45°，否则应设为48°，多普勒频率变化率的大小对信息检测性能影响较大，当多普勒频率变化率绝对值高于500 Hz/s时，信号检测门限会增加3 dB。

1 火星EDL过程中MFSK信号

    火星探测器EDL过程中直接对地通信采用一种特殊的多子载波调制体制^[2]，其信号是MFSK侧音信号，信号模型为：

    MFSK信号的频谱中存在着数据音的谐波分量，这些谐波分量是无用的，然而会占用一部分信号能量。进一步将信号中的数据音的功率细分为两部分：基波所占的能量P_dsc、多次谐波所占的能量P_dh。通过计算可知，在传输的总能量中，当Δ≈48°时，传输的载波能量P_T·cos²Δ正好等于数据音的基波分量所占的能量P_T·sin²Δ·8/π²。图1是Δ值为48°时MFSK信号的频谱图^[7]。

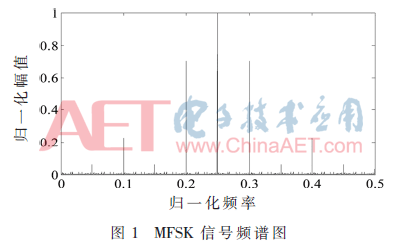
2 火星EDL过程中通信性能分析

2.1 仿真参数设置

    根据文献[13]可知，火星探测器在EDL过程中X波段直接对地通信的多普勒偏移范围(双向)大约为90 kHz，正向多普勒频率大约为50 kHz，多普勒变化率最大为700 Hz/s～1 200 Hz/s，多普勒频率的二阶导数大约为-25 Hz/s²～40 Hz/s²；共发出256个不同的数据音，每隔10 s切换发射的数据音。设定为基带仿真，仿真的采样率设为F_s=100 kHz，信号参数设置如表1所示。

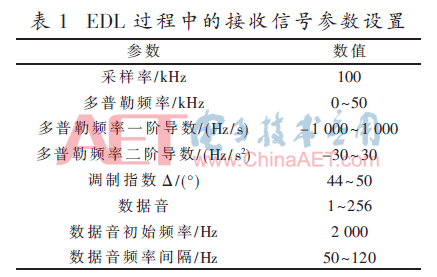
    每次仿真1 000 s，每隔10 s发送一个[1，256]之间的随机数据音，信号在EDL过程中的多普勒频率、多普勒频率变化率、多普勒二阶导数等参数，参照文献[7-8]中MER和MSL的动态范围进行设置。假设初始多普勒频率为20 kHz、初始多普勒频率变化率为-250 Hz/s，仿真动态范围精确到多普勒二阶导数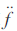，仿真产生火星探测器EDL过程中接收到的信号。

    EDL过程中的多普勒动态包络和数据音的设置如图2所示。其中150 s～300 s之间的高动态是火星探测器进入火星大气层时，剧烈的大气摩擦所致，图2(b)、(c)中500 s左右的尖峰是降落伞打开时火星探测器产生的剧烈抖动。

    根据火星探测器在EDL过程中的不同阶段，利用文献[7-8]中介绍的TDMAP算法进行载波频率的捕获、跟踪，以及信息的解算。利用TDMAP算法进行信号检测时，部分参数如表2所示。

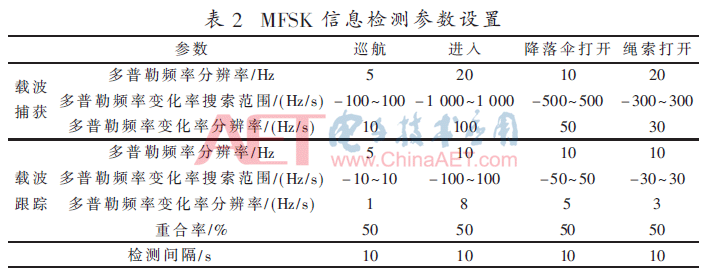
2.2 数据音频率间隔对信息检测性能的影响

    数据音之间的频率间隔主要受到载波捕获/跟踪阶段多普勒频率、多普勒频率变化率分辨率和信号带宽的影响，理论上数据音的频率间隔只要大于频率搜索精度就能完成信息检测。

    将调制指数设为48°，考虑到信息检测过程中载波捕获/跟踪的频率分辨率以及实际信号带宽，数据音频率间隔分别设为50 Hz、60 Hz、70 Hz、80 Hz、90 Hz、100 Hz、110 Hz、120 Hz。每个数据音频率间隔下重复仿真100次，得到载噪比为16 dB-Hz～20 dB-Hz时的信息误检率，如图3所示。

    通过仿真结果可以看出：不同数据音频率间隔时，MFSK信息检测性能几乎相同，因此相邻数据音之间的频率间隔对信息检测性能的影响较小。当数据音频率间隔为80 Hz时，它的信息检测门限为18.75 dB-Hz，较其他的检测门限稍低。综合考虑信号带宽，建议相邻数据音的频率间隔设为80 Hz。

2.3 调制指数对信息检测性能的影响

    由式(4)、(5)可知，减小调制指数，载波将占有更多功率，有利于载波的频率捕获/跟踪，但是数据音占有的功率相应减少，不利于数据音的解算。因此当信号多普勒动态较大、信噪比较低时，合理地分配载波与数据音的基波分量所占有的功率有利于提高信息的解算性能。

    将数据音频率间隔设为80 Hz，调制指数分别为44°、45°、46°、47°、48°、49°、50°，每个调制指数下重复仿真100次，得到载噪比分别为16 dB-Hz～20 dB-Hz时的数据音误检率。图4为调制指数分别为45°和48°时MFSK信息检测结果。

    从图4可以看出：当载噪比为16.25 dB-Hz和16.5 dB-Hz，调制指数为48°时误检率较高的数据音比45°时多了第3、11、12、45、61、66、85、86、88个数据音；当载噪比为19.5 dB-Hz和19.75 dB-Hz时，调制指数为45°仍会在第21、30个数据音发生误检，而调制指数为48°时则没有发生误检。综合分析可得，载噪比低于17 dB-Hz时，把调制指数设为45°更利于信息检测，当载噪比高于17 dB-Hz时，把调制指数设为48°更利于信息检测。

2.4 多普勒频率变化率对信息检测性能的影响

    根据火星探测器EDL过程中发射信号多普勒频率变化率绝对值的大小，将多普勒动态划分为3个级别，其中第一、二、三级分别为多普勒频率变化率的绝对值为0～100 Hz/s、100 Hz/s～500 Hz/s、500 Hz/s～1 000 Hz/s之间。将调制指数设为48°，数据音频率间隔设为80 Hz，载噪比分别为11 dB-Hz～20 dB-Hz，间隔为0.25 dB，其余仿真参数如表1和表2所示，重复仿真100次，得到不同载噪比下3种多普勒动态时的信息检测结果，如图5所示。

    从图5可以看出，多普勒频率变化率绝对值在0～100 Hz/s、100 Hz/s～500 Hz/s、500 Hz/s～1 000 Hz/s时的信息检测门限大约为15 dB-Hz、16.25 dB-Hz、19.5 dB-Hz，因此多普勒频率变化率的动态范围对信息检测性能影响较大。

3 结束语

    本文针对火星探测器在EDL过程中直接对地通信链路采用的MFSK通信方式，研究了MFSK调制指数、数据音频率间隔以及载波捕获/跟踪阶段多普勒频率变化率的大小对信息解算性能的影响。根据研究结果，得出以下结论：

    (1)相邻数据音之间的频率间隔对检测性能的影响较小，综合考虑信号带宽，建议相邻数据音的频率间隔设为80 Hz。

    (2)合理分配载波与数据音所占能量，有利于提高信息检测性能，当载噪比低于17 dB-Hz时，将调制指数设为45°，否则将调制指数设为48°，更有利于信息检测。

    (3)多普勒频率的大小对信息的正确检测没有影响，多普勒频率变化率的大小对信息的检测检测性能有较大影响；多普勒频率变化率在500 Hz/s以上时数据音的检测门限要提高3 dB。

由于载波捕获/跟踪时只考虑了多普勒频率、多普勒频率变化率，没有考虑多普勒频率的二阶及高阶导数，如何定量分析多普勒频率的二阶导数对信息检测性能的影响是下一步的研究方向。

参考文献

[1] KORNLELD R P，UARCIA M D，CRAIG I E，et al.Entry，descent，and landing communications for 2007 Phoenix Mars Lander[J].Journal of Spacecraft and Rockets，2008，45(3)：534-547.

[2] BRIAN C S，MELISSA S，PETER I.Telecommunications performance during entry，descent，and landing of the mars science laboratory[J].Journal of Spacecraft and Rockets，2014，51(4)：1237-1250.

[3] VILNROTTER V A，HINEDI S，KUMAR R.Frequency estimation techniques for high dynamic trajectories[J].IEEE Transactions on Aerospace and Electronic Systems，1989，25(4)：559-577.

[4] LI Y，FU H，KAM P Y.Improved，approximate，time-do-mam ML estimators of chirp signal parameters and their performance analysis[J].IEEE Transactions on Signal Processing，2009，57(4)：1260-1272.

[5] FARQUHARSON M，O′SHEA P，LEDWICH G.A computational1y efficient technique for estimating the parameters of polynomial-phase signals from noisy observations[J].IEEE Transactions on Signal Processing，2000，53(8)：3337-3342.

[6] CATTIVELLI F S，ESTABROOK P，SATORIUS E H，et al.Carrier recovery ehancement for maximum-likelihood Doppler shift estimation in mars exploration missions[J].IEEE Journal of Selected Topics in Signal Processing，2008，2(5)：658-669.

[7] SATORIUS E，ESTABROOK P，WILSON J，et al.Direct-to-earth communications and signal processing for mars exploration rover entry，descent，and landing[R].Reston：The Interplanetary Network Progress，2003：42-153.

[8] SORIANO M，FINLEY S，FORT D，et al.Direct-to-earth communications with mars science laboratory during entry，descent，and landing[C].IEEE Aerospace Conference，Big Sky，MT：AERO，2013：1-14.

[9] 甘浩，张晓林，马月红，等.一种改进的深空高动态微弱信号频率捕获算法[J].遥测遥控，2015，36(4)：6-11.

[10] 段瑞枫，刘荣科，周游，等.一种低复杂度的极低信噪比高动态信号载波粗捕获算法[J].航空学报，2013，34(3)：662-669.

[11] LOPES C G，SATORIUS E，ESTABROOK P，et al.Efficient adaptive carrier tracking for mars to earth communications during entry，descent and landing[C].IEEE/SP 14th  Workshop Signal Processing.Madison，WI：IEEE SSP，2007，1：517-521.

[12] LOPES C G，SATORIUS E，SAYED A H.Adaptive carrier tracking for mars to earth communications during entry，descent and landing[C].Proc.of 40th Asiomar Conference on Signal and Computers.Pacific Grove，CA：IEEE ACSSC，2006：1042-1046.

[13] KORNFELD R P，PRAKASH R，DEVEREAUX A S，et al.Verification and validation of the mars science laboratory/curiosity rover entry，descent，and landing system[J].Journal of Spacecraft and Rockets，2014，51(4)：1251-1269.

作者信息:

张天胜1，张晓林1，李  赞2

（1.北京航空航天大学 电子信息工程学院，北京100191；2.北京跟踪与通信技术研究所，北京100094）