0 引言

    海杂波环境下的小目标检测在航行安全、灾害搜救、海岸管理和国土安全等方面具有重要实际意义，利用电磁波对海上目标进行实时、可靠和自动化搜索也成为当前的研究热点。

    但海洋小目标检测面临严峻挑战：海杂波建模困难；小目标信杂比较低，速度较慢，多普勒域易被海杂波掩盖^[1]。近年来，国内外学者围绕该课题展开的研究主要分为下面几类。(1)基于统计模型的恒虚警(Constant False Alarm Rate，CFAR)检测方法^[2]：对海杂波建立不同的统计模型，通过实时估计杂波背景产生自适应门限进行检测处理；随着雷达分辨率的提高，非高斯模型下的恒虚警检测器由此诞生。(2)基于混沌^[3]、分形^[4]和神经网络^[5]的检测方法：HAKYIN S教授率先发现了海杂波的混沌特性^[3]，但对杂波的混沌模型目前尚存争议；HU J 等人证明了海杂波的分形行为^[4]，但分形目标检测算法对相位信息未有效利用；LEUNG H等人利用神经网络的非线性逼近特性，通过预测误差实现目标检测^[5]，但需很高的训练精度。(3)自适应匹配算法^[6]：基于海杂波球不变随机向量(Spherical Invariant Random Vector，SIRV)模型，通过估计杂波协方差矩阵实现目标检测，但需解决信噪比损失和积累样本数间的矛盾。(4)基于时频分析的目标检测方法^[7]：描述了信号在时频域的变化情况，如短时傅里叶变换和小波变换等，但其分析能力会受到基函数的影响。

    本文借助岸基微波雷达平台和相应的实测数据展开研究，并基于经验模式分解（Empirical Mode Decomposition，EMD）实现目标检测。EMD 算法对信号的分析是基于时域信号本身，不需要基函数，但其在目标检测中的运用需实现模态分量的自动筛选和判别^[8]。文中算法结合特征谱分析实现基于EMD的自适应目标检测。

1 基于模态函数特征谱的目标检测算法

1.1 EMD算法

    EMD算法能够根据信号的局部极值点自适应地对信号进行分解，分解出来的内模函数(Intrinsic Mode Function，IMF)分量可代表一种简单振荡，所在频带随着分解层次的增加逐渐降低。对于信号x(t)，可由EMD算法分解得到n个内模函数分量hi(t)和一个剩余分量r_n(t)^[8]：

1.2 模态函数特征谱

    由EMD算法分解出的模态函数频率逐渐降低，含目标的IMF分量可由人为筛选而检测出来，但如何自动筛选和判别是实现算法自适应性的关键。包含目标IMF与纯海杂波的多普勒谱差异是含有尖峰单频信号，可对其进行谐波分析^[9]。在驻留时间较短的条件下，雷达回波可近似认为是由有限单频信号叠加而成： 

其中，L为回波信号中包含的谐波次数，w(n)是均值为0、方差为σ²的复高斯白噪声，φ_i为初始相位。样本长度为K，则回波自相关阵为：

1.3 算法流程

    基于模态函数特征谱的海洋小目标检测算法流程如图1所示。首先，对雷达回波利用复数EMD进行分解；然后对得到的各个内模分量提取相关矩阵，特征值分解得到特征谱，并根据特征谱分布情况得到散布特征；最后基于散布特征在各个内模函数间的分布差异实现自适应目标检测。

2 实测数据处理

2.1 实测数据来源

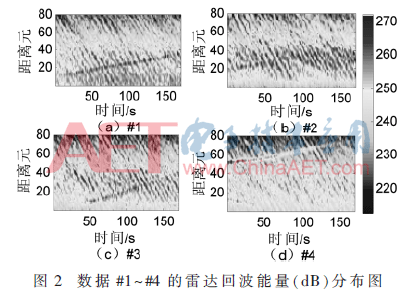
    实测数据来自武汉大学无线电海洋遥感实验室自主研制的微波多普勒雷达(Microwave Ocean Remote SEnsor，MORSE)^[10]。2012年底，MORSE雷达在中国南海的遮浪岛进行一个多月的海边试验，工作频率设为2.85 GHz，采用调频中断连续波，探测范围200 m~2 km，距离分辨率7.5 m。选取含慢速弱小目标的4组数据#1~#4，其包含80个距离元，持续时间171 s，环境参数和目标信息如表1所示，能量分布如图2所示。其中，海浪参量来自浮标数据，目标是附近来往的慢速小船只，能量较弱。

2.2 实测数据处理过程和检测结果

2.2.1 基于EMD的传统目标检测算法

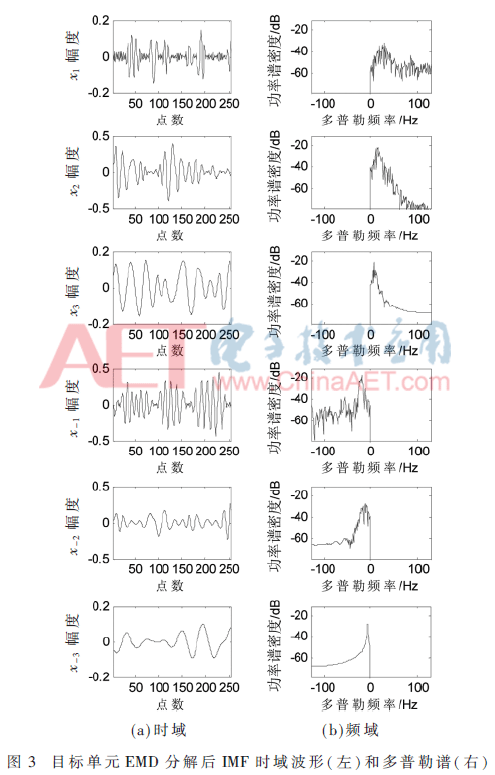
    从数据组#1中选取包含移动目标的一段数据，其来自第15距离元中第30 s~31 s时间段，包含256个点。对数据进行EMD分解，如图3所示，左侧是前3个正负IMF的时域波形，右边是相应多普勒频谱。从IMF分量的波形图可以看出，EMD分解所得的正、负IMF分量的频率依次降低。而且目标存在于x_-1中，可用x_-1重构目标回波信号，实现海杂波抑制和目标检测。

    按照复数 EMD中的信号重构方法，得到如图 4所示的原始信号和重构信号的时频域波形图。其中，左图是时域波形，右图是其多普勒谱。观察发现，经过 EMD 分解-分量筛选-信号重构这一过程，频率分量中的海杂波成分被剔除，只留下目标分量和基底噪声。

2.2.2 模态特征谱

    为实现含目标模态函数的自适应选择，现在对EMD分解得到的模态函数分别进行特征值分解得到其相应的特征谱，如图5显示了#1中海杂波和目标单元前3个正负模态特征谱的分布情况。

    由于目标的多普勒频移，x_-1的特征谱发生了明显变化；海杂波能量主要分布在x₁之中，故目标和海杂波的特征谱差异主要体现在正负第一个模态分量上。如图5所示，相对海杂波而言，含目标的模态分量x_-1的谐波成分相对较少，故在特征值分布中，大特征值的个数相对较少。根据式(8)计算累积贡献率达90%的大特征值个数，提取散布特征，其在内模函数上的分布如图6所示。

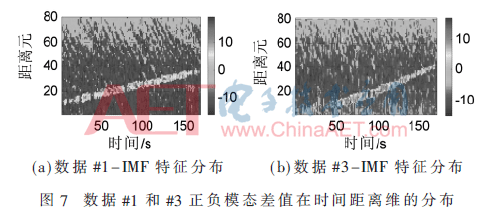
    观察发现，目标的存在使得x_-1和x₁间的差异增大，而且在负频模态函数中，散布特征依次递减的单调性被改变。再结合目标和海杂波单元的差异，提取正负模态差值作为检测量，其在整场数据的分布情况如图7所示。接着对其进行自适应门限检测，得到点迹分布图。

    为了与本文算法检测结果形成对比，这里给出传统恒虚警算法检测结果。传统恒虚警检测包括两个关键因素：(1)检测参量；(2)CFAR检测阈值。基于CFAR检测器的基本结构，提取不同检测参量，就形成了不同的CFAR目标检测算法[7，11]。若将峰值（方案1）和频域峭度（Frequency-Domain Kurtosis, FDK）（方案2）分别作为检测参量，就形成本文算法的对比方案，如图8所示。本文算法和传统算法中的方案1的检测结果如图9所示。观察点迹分布可以发现，由于目标慢速且弱小，传统算法检测能力受限，本文算法的检测概率相对较高。

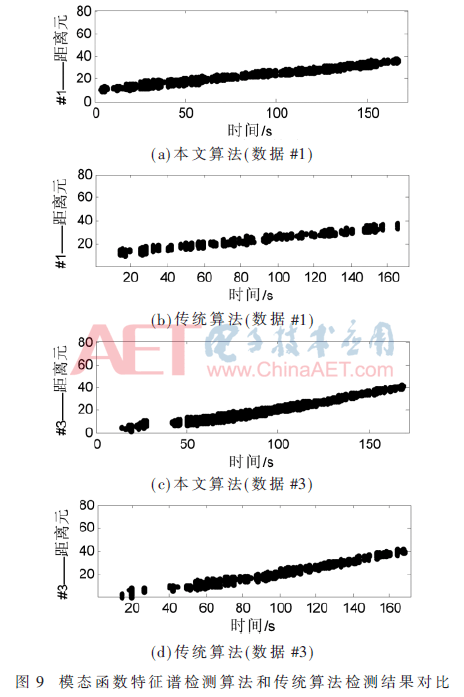
    对#1~#4进行检测处理，虚警率为0.001时检测概率如表2所示，对比发现，相对传统CFAR检测算法，本文算法的检测概率相对较高。以上实测数据处理结果说明，基于模态函数特征谱的检测算法可以实现海洋小目标的有效检测。

3 结论

    经验模态分解算法用于分析非线性信号，其分解过程是基于时域信号本身的局部特征，不需要基函数，其在海杂波抑制和目标检测方面具有应用潜力，但如何实现模态函数自动筛选和判别是算法的关键问题。而本文基于模态函数特征谱的检测算法有效解决了此问题，实现了基于EMD的目标检测算法的自适应性。在实测微波多普勒雷达数据中应用该算法，并与传统的恒虚警算法进行对比，结果表明：相对传统算法，文中算法不需要杂波抑制预处理环节，且在相同的虚警率约束下，提高了目标的检测概率。这为微波雷达海洋小目标检测提供了新的解决方法。

参考文献

[1] 何友，黄勇，关键，等.海杂波中的雷达目标检测技术综述[J].现代雷达，2014，36(12)：1-9.

[2] DONG Y.Optimal coherent radar detection in a K-distributed clutter environment[J].Iet Radar Sonar and Navigation，2012，6(5)：283-292.

[3] HAYKIN S，Li X B.Detection of signals in chaos[J].Proceedings of the IEEE，1995，83(1)：95-122.

[4] HU J，TUNG W W，GAO J.Detection of low observable targets within sea clutter by structure function based multifractal analysis[J].IEEE Transactions on Antennas and Propagation，2006，54(1)：136-143.

[5] LEUNG H，DUBASH N，XIE N.Detection of small objects in clutter using a GA-RBF neural network[J].IEEE Transactions on Aerospace & Electronic Systems，2002，38(1)：98-118.

[6] SHUI P L，LIU M.Subband adaptive GLRT-LTD for weak moving targets in sea clutter[J].IEEE Transactions on Aerospace & Electronic Systems，2016，52(1)：423-437.

[7] 崔少鹏.基于时频分析的海杂波背景下目标检测[D].哈尔滨：哈尔滨工业大学，2014.

[8] 胡玲霞.EMD算法在雷达杂波抑制中的应用[D].西安：西安电子科技大学，2013.

[9] 李彦兵，杜兰，刘宏伟，等.基于信号特征谱的地面运动目标分类[J].电波科学学报，2011，32(12)：2848-2853.

[10] CHEN Z Z，FAN L G，ZHAO C，et al.Ocean wave directional spectrum measurement using microwave coherent radar with six antennas[J].Ieice Electronics Express，2012，19(9)：1542-1549.

[11] JIN Y，CHEN Z Z，FAN L G，et al.Spectral kurtosis-based method for weak target detection in sea clutter by microwave coherent radar[J].Journal of Atmospheric and Oceanic Technology，2015，32(2)：310-317.

作者信息:

陈泽宗1，2，杨  干1，赵  晨1，贺  超1

（1.武汉大学 电子信息学院，湖北 武汉430072；2.武汉大学 地球空间信息技术协同创新中心，湖北 武汉430079）