宋寅卯,王蓬,曹卫锋
(郑州轻工业学院 电气信息工程学院,河南 郑州 450002)
摘要:为解决两轮自平衡车因不同用户身高体重的差异造成系统模型不准确而带来控制器对系统控制稳定性能差的问题,将自抗扰控制技术运用到两轮自平衡车运动平衡控制中。首先采用拉格朗日方法建立两轮自平衡车动力学模型,然后针对系统的特性推导出实现两轮平衡车自平衡控制的自抗扰控制器控制律。最后,搭建两轮自平衡车控制系统的Simulink仿真平台,分别采用线性自抗扰控制和经典自抗扰控制方法进行了试验比较。试验结果表明:与经典自抗扰控制器相比,新的自抗扰控制器能够较好地适应身高体重变化的环境,较好地自主达到稳定运行状态。
关键词:自平衡车;模型不准确;自抗扰控制;Simulink仿真平台
中图分类号:TP368.1文献标识码:ADOI: 10.19358/j.issn.1674-7720.2017.10.004
引用格式:宋寅卯,王蓬,曹卫锋.基于自抗扰控制的两轮自平衡车控制系统仿真研究[J].微型机与应用,2017,36(10):11-14.
0引言
两轮自平衡车具有占地面积小、运动灵活和绿色环保节能等特点,可以在多种环境下获得应用,既可在拥堵狭窄的道路作为交通工具,也可以在大型商场或广场作为巡逻车等。两轮自平衡车系统是一种具有左右两轮且能自动保持平衡的类倒立摆系统,具有多变量、非线性及强耦合等不稳定系统所具有的特性[13]。与所有的平衡机器人一样,两轮自平衡车的核心问题是运动平衡控制的问题。而平衡的控制目标则通过主控制器对电机的驱动控制来实现,在此基础上进行系统的速度控制。但由于骑行者的身高体重不同,造成了两轮平衡车的系统建模不准确,带来了控制器对系统控制稳定性能差的问题[4]。针对该问题,不同的学者提出不同的方法[56]:传统LQR控制器能实现平衡控制,但系统的抗干扰能力较差且要求准确的数学模型;模糊自适应控制有良好的控制效果,但是模糊规则很难完全匹配;经典自抗扰控制也能达到要求,但参数比较多且整定比较麻烦。为了简化控制器设计并适应不同用户的骑行需要,本文运用自抗扰控制技术设计线性观测器状态反馈进行系统平衡控制,利用零极点优化配置进行系统速度环的调节,进而实现系统的稳定运行。利用MATLAB[7]对自抗扰控制算法进行仿真,并通过搭建两轮自平衡车控制系统仿真平台进行试验,获得了期望效果,成功验证了该方案的可行性与有效性。
1两轮自平衡车的动力学模型
两轮自平衡车系统比较复杂,很难准确地建立数学模型。为便于分析,忽略了实际环境中存在的风阻和摩擦力等因素的影响(仅考虑地面与车轮之间的滚动摩擦且不滑动),可将两轮自平衡车简化为如图1所示的物理模型[8],图中各参数的物理含义见表1。两轮旋转中心点为坐标系的原点,过原点且平行于路面指向车的前进反方向为y轴,过原点沿旋转轴指向前进方向的右侧为x轴,过原点且垂直于路面向上为z轴。两轮自平衡车系统具有三个自由度,即绕轮轴的前后摆动,在水平面内的平动和转弯运动。基于拉格朗日动力学建模,通过动、势能变化与广义力的关系,建立两轮自平衡车的动力学模型。
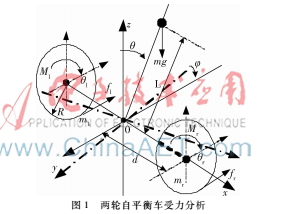

拉格朗日方程如下

其中:T为系统的总动能,qi为系统的广义坐标,Qi为系统的广义力。选取控制杆摆角为θ,左右车轮转角为θl、θr,作为广义坐标。整理可得到非线性系统方程如下:
![{W]8T_$}Z97VOL~@%7}1)1R.png {W]8T_$}Z97VOL~@%7}1)1R.png](http://files.chinaaet.com/images/2017/06/23/6363385481368654234944751.png)
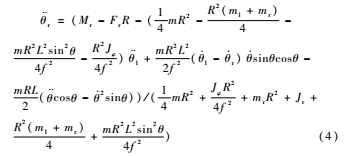
从以上建立的两轮自平衡车模型可知,由于不同用户和其他环境因素对自平衡车系统的影响不同,导致系统模型参数变化,控制器需要实时调整输出电机转矩使系统保持稳定[9]。
2线性自抗扰控制技术
自抗扰控制技术是由中国科学院韩京清教授提出的一种非线性控制律,其思想是采用一个扩张状态观测器来观测估计系统的扰动,使用简单控制进行抑制[10]。经典自抗扰控制器需要整定多个参数,限制了在实际中的应用。后来,高志强等人对此进行了改进,将所有的控制器和状态观测器都以线性化形式实现,得到了线性自抗扰控制器,取得了良好的实际控制效果[11]。线性自抗扰控制器(LADRC)由三部分构成:跟踪微分器、非线性PD控制器以及线性扩张观测器(LESO)。跟踪微分器的作用是根据控制目标和对象的承受能力先安排合适的过渡过程并给出此过程的微分信号。非线性PD控制器利用微分跟踪器输出和状态观测器输出组合生成控制信号。线性扩张状态观测器 (LESO) 是线性自抗扰控制中的核心部分,主要是补偿系统未建模部分和其他因素导致的系统变化。由建立的两轮自平衡车模型可知控制对象可以化为二阶的控制对象,应用一个二阶的自抗扰控制器实现控制,如图2所示。
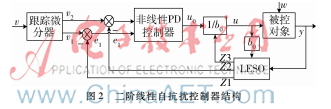
首先建立线性扩张观测器(LESO)
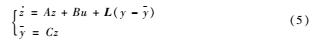
其中,L为状态观测器增益。设
L=[β1β2β3]T,误差ei=xi-zi,i=1,2,3,误差方程为
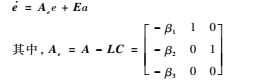
扩张状态观测器的特征方程为:
λ(s)=s3+β1s2+β2s+β3(6)

可通过极点配置的方法配置成理想特征方程λ(s)=(s+w0)3,求得β1=3w0,β2=3w20,β3=3w30,w0为观测器带宽。选取合适的状态观测增益β1、β2、β3,使逼近误差接近零,LESO就能实现对系统中各变量的实时跟踪。经过状态观测器之后的系统状态空间表达式为:

kp=w2c,kd=2ξwc,wc为控制器带宽频率,ξ为阻尼比。控制律的组成类似于PID, 不同的是将原来的积分换成了能够消除扰动的-z3/b0。另外wc和w0的关系满足w0=3~10wc,使得需要调节的系统参数只有kp、kd和b0三个参数,大大减少了自抗扰控制的参数,为便于实际应用奠定了基础。
3两轮自平衡车系统仿真建立
首先将式(2)建立以角度θ和角速度组成的广义二阶系统
![_F10@NBJ{DXO2@(]U3~_9JE.png _F10@NBJ{DXO2@(]U3~_9JE.png](http://files.chinaaet.com/images/2017/06/23/6363385501881127828316298.png)
其中,y为输出,f(x1,x2,w(t))为系统被控对象,包括系统确定、不确定动态和外界扰动w(t),u为系统输入,b为
给定的增益常数。对于式(9)所定义的系统,把车速当作系统外扰设计车体平衡环控制器。

将参数m=80 kg、R=0.2 m、mr=ml=3 kg、f=0.3 m、L=0.8 m代入系统模型方程。通过极点配置的方法设计速度环控制器,并选取极点为p=[-2,-2]求得反馈参数为k=[-2.592 2,-2.090 7]。最后,搭建以自抗扰控制器为控制核心的两轮自平衡车控制系统,针对不同的用户进行抗干扰、转弯和启动停止试验,并与经典自抗扰控制效果进行对比。
4仿真结果与分析
建立系统模型并进行封装,使用Simulink工具箱搭建以自抗扰为控制核心的两轮自平衡车仿真平台,编写M文件进行控制系统参数的传递。仿真情形为:在初始状态x=[0,0,0,0]T的情况下,给定一个角度为0.1 rad的前倾信号,并且在运行4 s时加入阶跃干扰,在7 s时对自平衡车给出转弯的指令。针对不同的用户进行仿真,试验结果如图3所示。
其中,实线为m=90、L=0.7 m时的系统响应曲线,点画线为m=90、L=1 m时的系统响应曲线,虚线表示m=80、L=1 m时的系统响应曲线。从图3的仿真曲线可以看出:当倾角信号给定后,系统在0.2 s内就达到了预期的平衡状态;当阶跃干扰发生时,系统也快速做出响应,并在0.8 s内重新达到平衡状态。而车速在接近4 s时达到理想速度,实现了小车的平稳启动;当阶跃干扰发生时,车速在0.8 s内重新达到稳定状态。在7 s时给定左转信号,右车轮的速度比左车轮的速度快,实现车体向左转弯,同理实现向右转弯。
与经典自抗扰控制进行试验对比,零时刻时给定一个0.7 rad的前倾信号,在质心距离为0.7 m、用户质量为90 kg的情况下进行仿真,仿真结果如图4所示。可以看出,系统的响应时间几乎相同,经典自抗扰控制下的响应曲线总在平衡位置小幅值波动,且对车速的控制效果差,而线性自抗扰控制下的系统稳定性较好,响应曲线较平滑。
5总结
试验结果表明本文所提出的以LADRC为核心配合极点配置的方案使两轮平衡车系统能够适应不同的用户,具有较快的响应速度和较强的鲁棒性,并且控制平稳超调量小,达到了预期效果。本文研究为后期硬件平台的实现打下了理论基础,具有一定的意义。
参考文献
[1] Xu Jianxin,Guo Zhaoqin,LEE T H.Design and implementation of a takagisugenotype fuzzy logic controller on a twowheeled mobile robot[J].IEEE Transactions on Industrial Electronics,2013,60(12):5717-5728.
[2] 阮晓钢,蔡建羡,李欣源,等.两轮自平衡机器人的研究与设计[M].北京:科学出版社,2006.
[3] 魏文,段晨东,高精隆,等.基于数据融合的两轮自平衡小车控制系统设计[J].电子技术应用,2013,39(5):79-80.
[4] 梁文宇,周惠兴,曹荣敏,等.双轮载人自平衡控制系统研究综述[J].控制工程,2010,17(S2):133-144.
[5] MADERO V, ARACIL J, GORDILLO F.A nonlinear control law for twowheeled selfbalanced vehicles[C].Melecon IEEE Mediterranean Electrotechnical Conference,2010:1557-1562.
[6] MADDAHI A, SHAMEKHI A H, GHAFFARI A.A lyapunov controller for selfbalancing twowheeled vehicles[J].Robotica,2014,33(1):1-15.
[7] 方璐,吴志刚,陈安钢.基于MATLAB的CSTR过程仿真控制研究[J].微型机与应用,2016,35(10):5-7.
[8] 屠运武,徐俊艳,张培仁,等.自平衡控制系统的建模与仿真[J].系统仿真学报,2004,4(16):839-841.
[9] 胡建,颜钢锋.基于自抗扰控制算法的两轮自平衡车分析[J].机电工程,2014,31(2):160-163.
[10] 韩京清.自抗扰控制器及其应用[J].控制与决策,1998,13(1):19-23.
[11] Zheng Qing, Gao Linda, Gao Zhiqiang. On validation of extended state observer through analysis and experimentation[J].Journal of Dynamic Systems Measurement & Control, 2012, 134(2):224-240.

