0 引言

    最近几年极化码在编解码领域中有突破性的进展，从而激起了极化码理论研究^[1]的快速发展。Arikan Erdal于2008年提出极化码^[1]，并在对称的二进制无记忆信道及任意的连续无记忆信道中证明了极化码相较于Turbo码^[2]和LDPC码^[3]更能达到香农极限^[4]，并且用极化码实现的通信系统能达到更高的通信带宽，所以极化码是目前公认的“最好”的码。

    目前，极化码的译码实现方式主要有软件和硬件两种方式，软件的实现方式因CPU串行工作模式限制了译码速度的提升，而FPGA因其具有快速并行计算的能力能弥补这一缺陷。此外，极化码的递归结构能够实现资源共享并简化计算过程，这一特点表明极化码易于FPGA实现^[5-6]。

    目前，关于极化码的译码算法主要有置信度传播(Brief Propagation，BP)算法^[7]、最大似然比(Maximum Likelyhood，ML)算法^[8]、连续消除(Successive Cancellation，SC)算法^[9]。这3种算法中，BP和ML算法由于在运算过程中涉及到较多的乘除法运算，因此不利于FPGA实现，而SC算法在译码过程中主要是通过加减和位运算实现，所以SC算法适用于FPGA实现。

    基于极化码、FPGA、SC译码算法3方面的优点，本文的重点工作是采用极化码、运用SC译码算法设计一种新型的译码器并在Xilinx XC5VFX70T上实现该译码器。

1 极化码的SC译码算法

1.1 SC译码算法

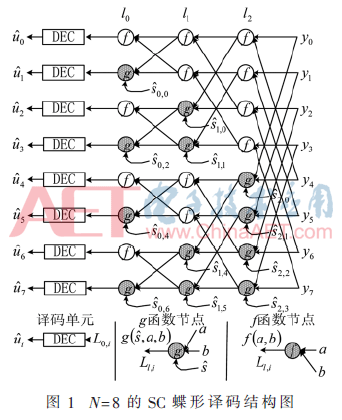
    SC译码算法的核心就是连续地估计每个比特的似然比值，Arikan表示这些似然比值^[9]可以通过数据流图采用递归的方式被有效地执行，这个数据流图类似于快速傅里叶变换结构，一般是通过蝶形结构的数据流图来计算似然比值，N=8的蝶形SC译码结构图如图1所示，y₀到y₇是信道的输出值，通过如下结构可得到译出码字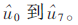

2 极化码译码的算法改进

2.1 SC译码算法结构的改进

    由图1可知由于数据之间的较强依赖性使得译码的效率不高，例如图1中l₂阶段的所有节点，当输入数据y0到y7准备完毕时允许节点执行相应的操作，而事实上在第一个译码时钟周期内只有前4个节点执行了相应的操作。为了比较译码效率，这里定义α表示使用率，表达式如式(4)所示：

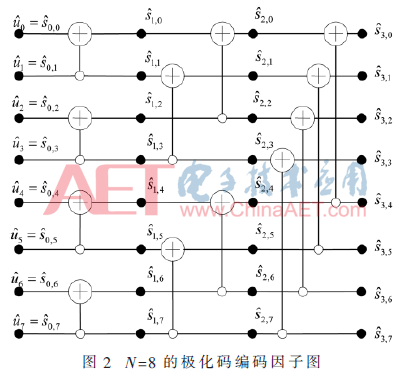
    随着码长的增加，使用率逐渐趋近于0，因此有很大的空间提升使用率。为了提升使用率，本文采用了线性的译码结构来改进蝶形译码结构。N=8的SC线性译码结构图如图3所示。

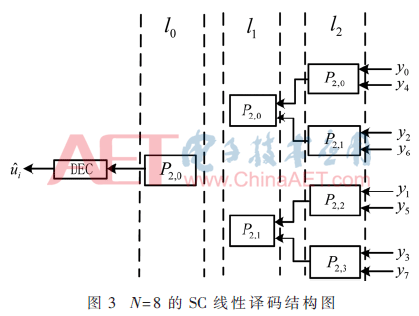
    在线性译码结构中，函数f和g一半码长的计算量都是在一个时钟周期完成的，用来存储部分计算结果和信道输出似然比的内存单元总共为2N-1个，在整个译码过程中的处理单元为N/2个。由式(4)可计算出线性结构译码算法的使用率如式(6)所示：

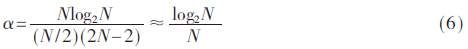
    可以看出相比于蝶形译码结构而言，采用线性译码结构的译码算法其使用率有一定的提升，并且这种结构编写的代码在硬件实现上更有利于综合布线。

2.2 SC译码算法在FPGA中实现的改进

    由式(2)可知函数f和g的计算涉及了乘法和除法，这在FPGA中实现会比较复杂，因此改进了最小和算法，在对数域中用等价函数来代替，等价式如式(7)、式(8)所示：

    由于信道的输出和运算过程中的值都是浮点数，这不利于在FPGA中实现，所以做了定点量化的改进，用(C，L，F)来表示量化结果，其中C代表信道输出的量化比特数，L代表运算过程中对数似然比的量化比特数，F代表信道输出和似然比值量化的小数位数。量化的位数不易过长，因为会消耗很多资源，也不易过短，因为会有很大的误差。本文做了包括(3，4，0)、(3，4，1)、(4，5，0)、(4，5，1)、(5，6，0)、(5，6，1)、(6，7，0)、(6，7，1)这些带小数位和不带小数位的多种不同位数的量化，通过实验结果的对比，选出了两种效果较好的量化方式分别是(4，5，0)和(5，6，1)，如图4所示为量化前后的BER曲线图。

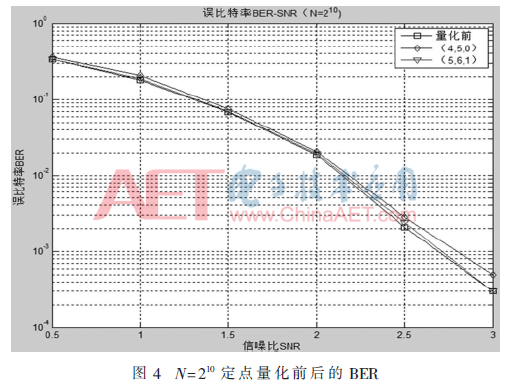
    由上图可知，(4，5，0)和(5，6，1)的量化结果与量化前相比对译码性能的影响都不大。再对比(4，5，0)和(5，6，1)的量化方式，由于选用没有小数位的量化方式更有利于硬件实现，因此本文选用(4，5，0)的量化方式。

    由图1可知，在译码过程中需要的存储单元总数为Nlog₂N个，随着编码块长度的增加，存储单元的总数也在增加，这样就会占用更多的FPGA的资源，所以采用了资源共享这一方式。本文中编码块长度N与阶段l的关系是l=log₂N-1，每一个阶段l需要的存储单元是2^l，因此实际只需要 N-1个存储单元即可。采用资源共享的方式并不会对译码的性能造成任何影响，并且大大地减少了存储单元的数量，节约了FPGA中的资源。

3 基于FPGA的极化码译码硬件平台与测试结果

    为了验证SC译码算法在FPGA上实现的正确性，本文首先在MATLAB中仿真对比了蝶形结构、线性结构以及算法改进之后的性能；然后用自行设计的以Xilinx公司的XC5VFX70T为核心处理器的14层电路板作为硬件平台，该平台最高运行频率可达550 MHz，片内时钟及存储等资源十分丰富，能够用来实现极化码的译码；最后给出了modelsim仿真波形和程序运行完成后chipscope抓取波形的对比结果。

3.1 基于MATLAB的译码仿真结果

    如图5所示为蝶形结构、线性结构和算法改进之后的SNR-BER曲线图。

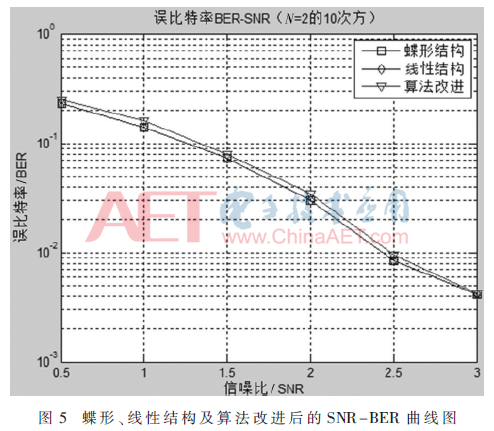
    由图可知使用蝶形结构的SC译码与线性结构的SC译码相比在不同信噪比的情况下误比特率是相同的，这是因为这两种结构只有在使用率方面有差异。对算法做了最小和、定点量化和资源共享改进之后，其性能有所下降，但差别不是很大，为了能够在硬件上更容易实现极化码的译码，做这些改进是值得的。

3.2 基于硬件平台的译码测试结果

    图6所示为码长256的仿真波形图和实际抓取的波形图。图中上半部分是model-sim的仿真波形，第一行是源码字，第二行是译出的码字，第三行是源码字和译出码字的异或结果。图中下半部分是chipscope波形图，对其进行了局部放大以便于观察，由于顺序不一样，因此用直线相连接。

    图7所示为码长1 024的仿真波形和实际抓取的波形图。图中上半部分是modelsim仿真图，第一行是源码字，第二行是译出的码字，第三行是源码字和译出码字的异或结果，由于码长太长，所以分成了4段显示。图中下半部分是chipscope抓取的波形，在波形中只放大了码字的开始和结尾部分，与仿真波形相比较时，其顺序是自下往上的。

    在工程综合编译完成之后会有一个设计的综合报告，会给出编译所使用的LUT、FF、RAM以及最大时钟频率，具体值如表1所示，通过式(9)可以计算出运行过程中的吞吐率。

    式中f_m为最大时钟频率，t_d为译码延迟的时钟周期数，即从译码开始至译码结束所使用的时钟周期数，N_A为有效码长。通过上式可以计算出编码块长度为256时吞吐率约为36.4 Mb/s，编码块长度为1 024时吞吐率约为34.2 Mb/s。

    不同编码块长度下的综合资源结果比较如表1所示。

    相同编码块长度下采用蝶形译码结构和线性译码结构的使用率结果对比如表2所示。

    从表2中可以看出随着码长的增加使用率在降低，但是在相同编码块长度下线性译码结构明显比蝶形译码结构的使用率要高一些。

4 总结

    本文针对当前极化码在整个通信领域的应用十分广泛的现象，主要研究了SC译码算法并在Xilinx XC5VFX70T芯片上实现，在设计过程中考虑了FPGA的资源占用情况、译码的复杂度以及译码使用率。该译码器高达145 MHz的时钟频率和36.4 Mb/s的吞吐率使得该译码器具有较强的工程实用性。

参考文献

[1] 陆婷婷.极化码的编解码研究及仿真[D].南京：南京理工大学，2013.

[2] KOVACI M，BALTA H.Turbo codes performance on Rice flat fading environment[C]//Electronics and Telecommunications(ISETC)，2014 11th International Symposium on.IEEE，2014：1-4.

[3] KUMAR N，PRAKASH C，SATASHIA S N，et al.Efficient implementation of Low Density Parity Check codes for satellite ground terminals[C]//Adva-nces in Computing，Communications and Informatics(ICACCI)，2014 International Conference on.IEEE，2014：689-695.

[4] KORADA S B，URBANKE R.Polar codes：characterization of exponent，bounds，and constructins[J].Information Theory，IEEE Transactions on，2010，56(12)：6253-6264.

[5] MISHRA A，RAYMOND A J，AMARU L G，et al.A successive cancellation decoder ASIC for a 1024-bit polar code in 180 nm CMOS[C]//Solid State Circuits Conference(A-SSCC)，2012 IEEE Asian.IEEE，2012：205-208.

[6] LEROUX C，TAL I，VARDY A，et al.Hardware archi-tectures for successive cancellation decoding of polar codes[C]//IEEE International Conference on Acoustics.IEEE，2011：1665-1668.

[7] HUSSAMI N，KORADA S B，URBANKE R.Perfor- mance of polar codes for channel and source coding[C]//Information Theory，2009.ISIT 2009.IEEE Intemational Symposium on.IEEE，2009：1488-1492.

[8] KAHRAMAN S，CELEBI M E.Code based efficient maximum-likelihood decoding of short polar codes[C]//Information Theory  Proceedings(ISIT)，2012 IEEE Intemational Symposium on.IEEE，2012：1967-1971.

[9] ARIKAN E.Channel polarization：A method for costructing capacity-achieving codes for symmetric binary-input memoryless channels[J].IEEE Transactions on Information Theory，2009，55(7)：3051-3073.

作者信息：

邓媛媛，卿粼波，王正勇，高菁汐，徐成强

（四川大学 电子信息学院，四川 成都610064）