陈少昌,任圣君,章耀文
(海军工程大学,湖北 武汉 430033)
摘要:目前,对于信号来源的定位与判断,主要的研究集中在通信和雷达信号研究领域,对于应用于电磁兼容现场测试中的干扰源定位方法的研究却很少,但是实际应用当中又需要在现场对干扰源进行定位。为此,针对电磁兼容现场测试中信号的特点,借鉴通信和雷达方面对信号来源进行定位的方法,提出一种基于盲波束形成的电磁干扰源定位方法。
关键词:盲波束;电磁兼容测试;电磁干扰故障诊断
中图分类号:TP306文献标识码:ADOI: 10.19358/j.issn.1674-7720.2017.10.025
引用格式:陈少昌,任圣君,章耀文.基于盲波束形成的电磁干扰源定位[J].微型机与应用,2017,36(10):89-91.
0引言
目前,非标准测试环境下的电磁兼容测试、电磁干扰故障诊断、电磁干扰源信号源定位逐渐成为电磁兼容测试信号处理迫切需要解决的重点和难点问题[13]。传统的电磁干扰源定位方法非常依赖专业人员的操作和判断。其先分离出环境背景噪声和干扰源噪声,得到测试系统电磁干扰信号的频谱,找出超标的频率点;然后采用排除法或依据对各个设备工作原理的了解,找出具体的干扰源[4]。但同一设备可能在多个位置产生同频率的干扰,不同的设备也可能在同一位置产生同频率的干扰,因此需要进行大量的测试试验。由于测试过程繁琐,测试数据复杂,使得判断困难,最终结果的准确性和效率都不高,误判的情况经常出现。
1基本原理
大型系统的电磁兼容现场测试信号通常是各种功能信号、背景噪声、干扰信号和各种反射信号相互叠加形成的混合信号,要实现电磁干扰源的定位,首先需要从测试得到的混合信号中分离出电磁干扰信号,最常用的就是盲源分离技术[5]。
盲源分离(Blind Source Separation,BSS)是指在源信号未知、混合系统冲击响应矩阵A未知的条件下,从观测的多通道混合信号中分离并恢复出各个源信号的过程。
如图1所示,盲波束形成(Blind Beam Forming)是指在没有信号方向或阵列流形等先验信息的条件下,得到波束形成器的权向量,实现信号的接收。

空间K个未知信号源s(n)=[s1(n)s2(n)…sK(n)]T通过空间传播(方向矩阵A表示),由M个阵天线接收,得到信号x(n)=[x0(n)x1(n)…xM-1(n)]T。盲波束形成的目的是,设计K个空域滤波器W=[w1w2…wK]∈CM×K,使滤波器的输出y(n)=WHx(n)=[y1(n)y2(n)…yK(n)]T为空间K个信号源的接收信号。因此,盲波束形成可以看成盲源分离的一个特例[6]。
2基于奇异值分解的降维预处理
设接收天线阵元数为M,信源个数为K对无噪声阵列接收信号模型,即:
x(n)=As(n)(1)
式中,矩阵A∈CM×K,信号向量分别为:
s(n)=[s1(n)s2(n)…sK(n)]T∈CK×1(2)
x(n)=[x0(n)x1(n)…xM-1(n)]T∈CM×1(3)
用N次快拍的数据构成如下的接收数据矩阵(设K≤M≤N):
X=AS(4)
式中,A∈CM×K,X和S为:
X[x(1)x(2)…x(N)]∈CM×K
S[s(1)s(2)…s(N)]∈CK×N(5)
假设K个信号源相互独立,即矩阵S是行满秩的;假设K个信号从不同的方向入射到阵列,即矩阵A是列满秩;且它们的秩都是信号源个数K。由矩阵理论可知,接收矩阵X=AS的秩也为信号源个数K。
对接收数据矩阵X进行奇异值分解,X应有K个非零奇异值,设这K个非零奇异值对应的左奇异向量构成的矩阵分别为S∈CM×K和S∈CN×K,则数据矩阵X可表示为:
X=AS=SSHS(6)
式中,S是由K个非零奇异值构成的对角阵, HSS=IK,HSS=IK 。
由于矩阵A和矩阵S都是秩为K的列满秩矩阵,因此存在可逆矩阵T∈CK×K,使得
S=AT(7)
如果存在噪声,阵列信号接收模型变为:
X=AS+E(8)
式中E∈CM×N是加性噪声矩阵。
由于噪声的存在,矩阵X是行满秩(其秩为M)的,而矩阵X的奇异值分解可表示为:
X=UΣVH=[SUN]S0
0NHS
HN
=SSHS+UNNHN(9)
式中,U∈CM×M和V∈CN×N分别是由左奇异向量和右奇异向量构成的酉矩阵。将M×M维对角矩阵Σ分块,S包含K个较大奇异值,包含信号和噪声的贡献,S和S分别是对应的左右奇异向量构成的矩阵;S包含M-K个小奇异值,仅有噪声的贡献,当不存在噪声时,N=0。
定义有噪声情况下观测信号矩阵X的截尾奇异值分解为:
X≈SSHS(10)
虽然S、S和S的维数与式(6)的情况一致,但它们与式(6)所定义的S、S和S之间有差别。在式(10)中,S和S只是无噪声情况下的S和S的近似,而S不仅与信号功率有关,还与噪声功率有关。
利用截尾奇异值分解式(10)对X进行预处理,可以减小噪声的影响。另一方面,截尾奇异值分解可以使处理的空间维数减小(从M维降至K维),从而降低运算量。
令W=[w1w2…wK]∈CM×K为需要设计的K个空域滤波器权向量构成的矩阵,wK是对信号sK(n)的空域滤波器权向量,左乘以式(4)两端,可得到波束形成器输出为:
Y=WHX=WHAS(11)
由于X=AS,利用关系式S=AT,有X=ST-1S,且HSS=IK,可得:
S=THSX(12)
当空域滤波器W满足W=HSS时,波束形成器Y=S,故空滤滤波器W应为:
W=STH(13)
其中矩阵S由接收数据矩阵X进行奇异值分解获得,那么,要得到盲波束形成权值矩阵,还需要求出满秩矩阵T[7]。下面介绍基于ESPRIT算法[810]求矩阵T的方法。
3基于ESPRIT算法的盲波束形成
考虑由M个阵元组成的均匀线阵,K个远场窄带信号从θ1,θ2,…,θK方向入射到阵列。无噪声时N次快拍的接收数据矩阵为(设K≤M≤N):
X=AS(14)
式中X∈CM×N,A∈CM×K,S∈CM×N。
分别取A的前M-1行和后M-1构成矩阵A1和A2,且有:
A2=A1Φ(15)
对角阵Φ定义为:
Φ=diag{e-jφ1,…,e-jφK}(16)
式子(15)可用选择矩阵表示:
J2A=(J1A)Φ(17)
其中选择矩阵定义为:
J1=[IM-101]∈C(M-1)×M
J2=[01IM-1]∈C(M-1)×M(18)
根据公式(10),对X进行截尾奇异值分解预处理,有:
X≈SSHS(19)
存在可逆矩阵T∈CK×K使得S=AT。
1=J1S=A1T
2=J2S=A2T=A1ΦT(20)
所以:
2=A1(TT-1)ΦT=1T-1ΦT(21)
利用ESPRIT的方法通过特征值分解的方法进行求解[11]。当阵元数大于信源个数时,即K≤M-1时,1是列满秩矩阵,矩阵H11可逆,存在左逆矩阵1=(H11)-1H1,使得
12=T-1ΦT(22)
由于Φ是对角矩阵,而T是可逆矩阵,这样可以通过对矩阵12进行特征分解,得到特征值构成的对角矩阵Φ,以及对应的特征向量构成的矩阵T-1。
于是通过ESPRIT算法,便可得到满秩序矩阵T。由此可得盲波束形成器权矩阵为:
W=STH(23)
且波束形成器的输出为:
Y=WHX=THSX(24)
4仿真实验
设接收阵列为16阵元的均匀线阵,间距为1/2最短信号波长。设空中有3个不同的信号,数学形式如下:
SEUT(t)=A0sin2πf0t+n(t)
Sjam1(t)=A1sin2πf0t+n(t)
Sjam2(t)=A2sin2πf1t+n(t)(25)
其中A0=2*A1,A1=A2=1,f0=400 MHz,f1=300 MHz。EUT信号的来波向为20,干扰信号来波方向分别为10、30,n(t)是空间中的白噪声和各个阵元上的加性噪声,信噪比为10 dB。使用MATLAB软件平台进行基于ESPRIT盲波束形成一维干扰源定位仿真实验,结果如图2所示。将信号的来波方向改为二维的,EUT信号的来波向为(5,20),干扰信号来波方向分别为(15,25)、(20,15),进行基于ESPRIT盲波束形成二维干扰源定位仿真实验,结果如图3所示。
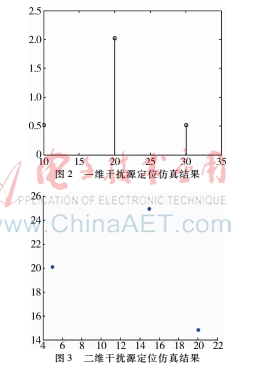
从图2和图3中可以看出,基于ESPRIT的盲波束形成的干扰源定位方法能够较为准确地定位到实验中预设的干扰的坐标。该方法从阵列接收到的信号中得到的混合矩阵,其中包含信号从干扰源到阵元之间的空间传播函数,从中可以计算出阵元到干扰源之间的距离等参数,从而进行干扰源的定位。仿真实验的结果证明了该方法的有效性。
5结论
本文介绍了基于ESPRIT盲波束形成的干扰源定位原理,将盲源分离理论运用到干扰源定位中,在被测试设备周围设置阵列接收混合信号,使用基于ESPRIT算法盲波束形成方法得到的混合矩阵,从中可以得到阵元到干扰源之间的距离等参数,从而进行干扰源的定位。在仿真实验中,使用MATLAB分别进行了一维和二维的干扰源定位实验,从实验结果可知,该方法可以准确定位干扰源的位置,证明了该方法的可行性。
参考文献
[1] 何滴露. 基于恒模特性的盲波束形成算法研究[D]. 沈阳:东北大学, 2012.
[2] 何振亚, 陈宇欣. 一种基于特征空间的盲波束形成算法[J]. 数据采集与处理, 1999, 14(3): 263-266.
[3] 程君佳, 田书林, 李力. 电磁干扰源的相关性定位测试方法研究[J]. 中国测试技术, 2007, 33(2): 42-44.
[4] 邢钟化. 基于函数逼近径向基函数网络的盲波束形成算法的研究[D]. 太原:太原理工大学,2008.
[5] 范达. 基于信号循环平稳性的盲算法研究[D]. 郑州:中国人民解放军信息工程大学,2003.
[6] 姚广平, 陈健东. 工业现场测控系统的电磁干扰分析与对策[J]. 微型机与应用, 2009,28(19): 72-74.
[7] 张应慧. CDMA系统中基于恒模特性的盲波束形成算法研究[D]. 太原:太原理工大学,2008.
[8]金晖, 罗敏, 刘忠. 窄带 HPM 强电磁环境中控制系统的 EMC 分析和设计[J]. 电子技术应用, 2016,42(6): 77-80.
[9] 张才霞. 基于阵列天线空域目标波束形成研究[D]. 南京:南京航空航天大学,2012.
[10] 刘文彦, 邓新中. 测试系统中干扰及其形成机理[J]. 电子技术应用, 2002, 28(10): 44-46.
[11] 吴小强. 基于 ESPRIT 算法的二维 DOA 估计方法研究[D]. 哈尔滨:哈尔滨工程大学, 2008.

