0 引言

    随着智能终端的快速发展及其在无线通信网络中的广泛应用，无线数据传输速率需求呈现指数增长，至2020年，无线通信的传输速率需求将是目前传输速率的近千倍，能够提供每秒千兆比特传输的4G移动通信系统仍然难以满足这种需求。因此，有学者提出了大规模MIMO的概念^[1]，即在基站端部署上百根天线来服务几十个终端。对于一个非常大的天线阵列，信道状态由随机变为统计确定。其结果是小尺度衰弱能够被平均。此外，随着基站天线数目的增加，不同用户信道矢量之间近似正交,当天线数目趋于无穷时,不同用户信道矢量之间趋于正交。若天线数量无限制，在BS端进行简单的匹配滤波处理(Matched Filtering，MF)，不相关的噪声和小区内干扰可完全抑制^[1]。大规模MIMO系统的另一个重要的优势是能够降低发射功率。在上行链路中，减少终端的发射功率有助于减缓电池的耗尽速度。在下行链路中，基站端的功率放大，电路及冷却系统耗费了主要的功率。因此，减少发射的射频功率将有助于减少基站的功率消耗。

    大规模天线阵列可实现大规模MIMO的巨大潜力激发了研究者的兴趣及其相关技术研究。现有的主要研究集中在以下几个方面：(1)大规模天线阵列的设计^[2]；(2)信道的建模和估计^[3]；(3)频谱效率和能量效率的权衡分析^[4]；(4)预编码方案^[5]；(5)信道估计和检测算法^[6]；(6)导频的设计以及分配方案^[7]。

    在上行链路中的研究中，文献[8]证明了能量效率是关于天线数量M的拟凹函数。在下行链路中文献[9]说明了能量效率是关于M的拟凹函数。但是上述文献得出结论的过程中没有综合考虑M和K 对最大化能量效率的影响，或者能量效率的推导建立在简单的功率消耗模型上。对于给定上行和速率，文献[10]获得了最佳的M和K，由于没有考虑导频信号的开销，从而使得获得的K值很大。为了获取更准确的结果，本文使用一种典型的MIMO功率消耗模型，通过该模型来说明实际的功耗扩展速度大于随线性增长的M和K。基于此模型洞悉多用户大规模MIMO系统中M、K和发送功率对总的上行和下行能量效率的影响。

1 系统模型

    考虑单小区系统，小区内有K个用户。基站拥有M根天线服务于单天线用户。带宽为B(Hz)，采用的是平坦衰落，相干带宽为B_C(Hz)，相干时间为T_C(s)。所以在一个相干块U=B_CT_C的长度内，信道特性保持不变。假设基站和用户之间完全同步，并且两端采用TDD方式进行通信，上下行发送的数据结构如图1所示。上行和下行码元发送比例是ζ^(ul)和ζ^(dl)，并且ζ^(dl)+ζ^(ul)=1，上行链路中导频信号占用Kτ^(ul)个码元，τ^(ul)≥1。由于采用TDD方式进行通信，所以基站可以充分利用信道的互易性，由上行信道的估计来进行信号接收以及下行信号预处理。

1.1 信道模型和预编码

1.2 上行链路

其中，第一项表示期望信号，第二项表示小区内来自其他用户的干扰，第三项表示噪声。p_d表示每个用户的平均发送功率，满足p_d=ρK。s=[s₁，s₂，…，s_K]^T为K个用户同时发送的信号矢量。

    采用ZF检测器时，第k个用户的信干比(Signal to Interference Ratio，SINR)为：

1.3 下行链路

1.4 实际功率消耗消耗模型

    现有的大多数关于大规模MIMO能量效率的研究中，选取的功率消耗模型主要包括发射功率和设置为常数的电路消耗功率。然而当基站天线数目趋于无穷时，使用这种简单的模型会导致能量效率随着基站天线数目的增加也无限增长。产生这种结果的主要原因是由于电路当中射频(Radio Frequency，RF)和基带处理所消耗的功率会随着M和K的增加而变化。因此在传统的MIMO中由于收发两端的天线数目较少，可以将电路消耗的功率设置为常数。然而在大规模MIMO系统中并不适用。本文使用文献[11]提出的典型MIMO收发器电路功率消耗模型：

    该模型分为两部份，固定功率P_FIX为常量，表示控制信号、与负载无关的回程以及基带处理器的功率消耗；后面三项表示收发器的功率消耗，其中P_BS表示基站中每根天线的电路功率消耗包括转换器、混频器和滤波器三部分，P_SYN表示本地振荡所需要的功率，P_UE则表示用户端的放大器、混频器、振荡器以及滤波器的电路功率消耗。通过上述功率模型使分析得到的能量效率更接近真实值。

2 最大化能量效率

2.1 多小区系统中最大化能量效率

    大规模MIMO系统中的能量效率采用bit/Joule来衡量，即表示平均和速率(bit/second)与总共消耗的平均功率的比值(Watt)。在多用户环境中，采用ZF处理上行链路和下行链路来最大化能量效率可以表示为：

    本文通过最优的用户数目 K、天线数目 M和发送功率ρ来最大化能量效率。 K和 M是整数，从而可以通过穷举所有的( K， M)对并为每对分配最优的功率，以此来计算对应的能量效率。通过比较，找出能量效率最大时所对应的 K、M值。

    上述方法虽然简单，但是计算复杂度较大，它需要遍历所有 K和M可能组合的能量效率值然后进行对比从而解出最大值。一个实用的方案是根据标准的迭代算法优化系统参数，可以通过乘积对数函数^[12]来推导出每一次迭代的最优解M和ρ，而对于K作为自变量时，目标函数的求解不满足乘积对数函数的求解条件，所以K无法利用上述方法求解。由于能量效率是关于K的拟凹函 ，所以可以通过对目标函数求关于K的导数，进而求得最优的K值。具体的算法如下：

    (1)初始化M、K、ρ。

    (2)求解最优用户数量

    ρ^*的表达式中含有C′、D′两项，可以看出发送功率(PA)随着固定功率、基站天线和用户天线{P_BS，P_FIX，P_SYN，P_UE}的增加而增加，即天线数目增加时，由式(9)可知相应的电路消耗功率也会增加，而式(16)说明了电路消耗功率的增加会引起ρ^*的增加，从而提升和速率。所以当发射功率相对于总的消耗功率可以忽略不计时，通过提高电路消耗功率来最大化能量效率是可行的。从文献[13]的研究中可以得出，当基站无法获得准确的信道状态信息(CSI)时，随着M的变大，发送功率与成反比。然而，本文通过式(16)来说明通过文献[13]无法准确获得系统最优的能量效率。

    (5)重复步骤(2)～(5)，直到迭代完成。

    上述所求解的能量效率有上界。因此，设置任意的初始值M、K、ρ，通过迭代算法使每一次计算数值向最优的值逼近，并且在逼近的过程中，M、K、ρ的值只会增加(或保持),直到求得最终的解。   

2.2 多小区系统中最大化能量效率

    在多小区系统中采用与单小区相同的分析架构。假设所有小区中的M、K、ρ小区形状，用户分配方式以及传播环境都相同，即小区间完全对称。仿真中使用J个小区。记x_jk表示小区j中的第k个终端的位置，l_j(x)表示小区j中在位置x∈R²处用户和基站之间的信道衰减包括路径损耗、散射、阴影衰弱三部分。由于仿真中采用完全对称的方案表明在不同小区的同一位置处反向平均信道衰弱S_x=E{(l_j(x_jk))^-1}都相同。此外，定义：

用来表征小区l中的用户k对小区j的上行链路干扰。由于对称的原因，系统中上行链路和下行链路的干扰相同，即I_jl=I_lj。

    式(18)相对于单小区系统要复杂的多，由于文中考虑的参数K、M、ρ都出现在了分子和分母上，所以求解非常复杂。在这里本文将其放到单小区的系统模型中去求解，通过将式(18)代入到单小区系统中可取得与单小区相似的结果。

3 仿真分析

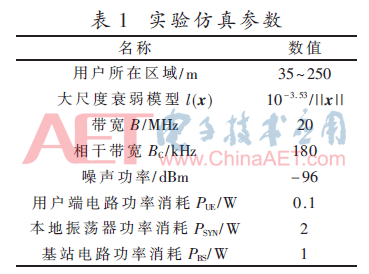
    本节中对前文提出的假设通过MATLAB仿真来证明。仿真中，上行链路和下行链路都采用ZF处理。本文分别分析了在单小区拥有好的信道状态信息时能量效率与发送功率的关系以及在多小区中导频污染对能量效率的影响。同时，分别给出了在两种模式下系统达到最大能量效率时所需要的基站天线数目，小区内所能服务的最大用户量和最佳发射功率。相应的仿真参数由表1给出。

    本文所考虑的多小区系统是完全对称的。用户的分配方式和单小区系统完全相同，小区的形状为正六边形，并且假定每个小区所受到的干扰只限于其每个方向上最近的一个小区。仿真中分别采用导频复用因子为1、4进行仿真。所有仿真结果如图2～5所示。

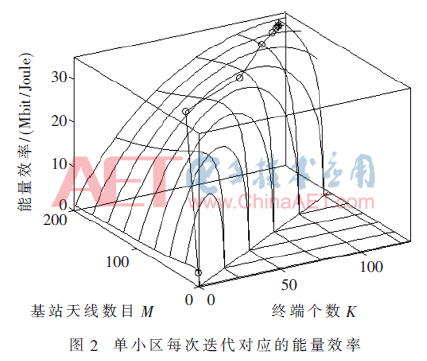
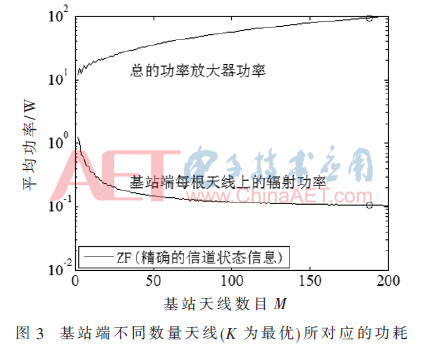
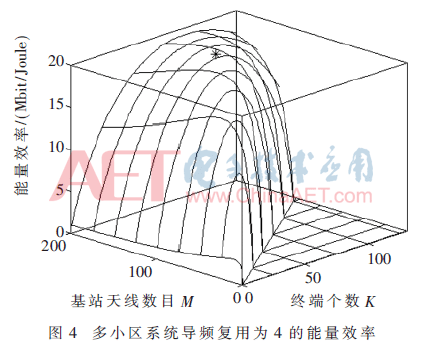
    图2和图3是对单小区性能的描述。图2表示当基站拥有完整的信道状态信息并使用ZF处理时，每次迭代产生的能量效率所对应的M和K。每组M和K所对应的最优ρ由式(15)求得。图中的*号表示全局最优点，可以看出图2的表面光滑并且是凹的，并且达到的能量效率为33.78 Mbit/Joule所对应的M=188，K=120。每次迭代的过程即为图中所标记的圆点，从图中可以看到大约经过5次迭代之后就已经非常接近最佳值点。

    图3表示的是使用不同M(K是最优的)最大化能量效率时候所消耗的PA功率，圆圈表示最大能量效率点。图中总的PA功率曲线随着M的增加而上升，说明当基站增加天线数目时，可以通过提高发射功率来最大化能量效率。同时图3给出了每根基站天线的发射功率随着天线数目的增加而减小，原因是总的发射功率虽然增加，但是由于M值较大，从而分配到每根天线上的功率就相对较小。

    图4～5为多小区的仿真结果。图4表示在多小区中最优的能量效率所对应的M和K的值，采用的导频复用因子为4，此时受到导频污染的可能性最小。尽管如此，在多小区系统中，目标小区所能达到的能量效率仅为单小区的一半。图5表示不同导频复用因子下的发射功率。图5和图3比较相似，只是在多小区的仿真中能够实现的能量效率减小。因此，小区间的干扰通过减少吞吐量减少了发送功率和能量效率。从图中可以看出，导频复用因子越高，受到的小区间干扰越小。同时随着天线数目的增加，仍然可以通过增加发送功率来提升能量效率。

4 结论

    本文针对现有大规模MIMO系统中的功率消耗模型只考虑了发射功率的消耗而忽视了电路功率消耗，或者仅将电路消耗功率作常数处理，不考虑随着硬件变化，相应的电路功耗也会随之改变。本文使用一种现有的功率消耗模型，基于该模型的能量效率是关于M和K的拟凹函数。通过对上下行链路进行ZF处理，联合M和K以及发射功率来最大化能量效率。在基站端配置上百根天线同时服务大量的终端，并且随着M和K的增加，可以通过提高总的发射功率来提升系统的能量效率。

参考文献

[1] MARZETTA T L.Noncooperative cellular wireless with unlimited numbers of base station antennas[J].IEEE Transactions on Wireless Communications，2010，9(11)：3590-3600.

[2] ALRABADI O N，TSAKALAKI E，HUANG H，et al.Beamforming via large and dense antenna arrays above a clutter[J].IEEE Journal on Selected Areas in Communications，2013，31(2)：314-325.

[3] FICKER T, MARTISEK D.Channel   measurements and analysis for very large array systems at 2.6 GHz[C].European Conference on Antennas and Propagation，2012：433-437.

[4] ZHAO L，ZHENG K，LONG H，et al.Performance analysis for downlink massive MIMO system with ZF precoding[J].Transactions on Emerging Telecommunications Technologies，2014，25(12)：1219-1230.

[5] YANG H，MARZETTA T L.Performance of conjugate and zero-forcing beamforming in large-scale antenna systems[J].IEEE Journal on Selected Areas in Communications，2013，31(2)：172-179.

[6] YIN H，GESBERT D，FILIPPOU M，et al.A coordinated approach to channel estimation in large-scale multipleantenna systems[J].IEEE Journal on Selected Areas in Communications，2012，31(2)：264-273.

[7] APPAIAH K，ASHIKHMIN A，MARZETTA T L.Pilot contamination reduction in multi-user TDD systems[C].IEEE International Conference on Communications，2010：1-5.

[8] HU Y，JI B，HUANG Y，et al.Energy-efficiency resource allocation of very large multi-user MIMO systems[J].Wire-less Networks，2014，20(6)：1421-1430.

[9] BJORNSON E，KOUNTOURIS M，DEBBAH M.Massive MIMO and small cells: improving energy efficiency by optimal soft-cell coordination[C].International Conference on Telecommunications，2013：1-5.

[10] MOHAMMED S K.Impact of transceiver power consumption on the energy efficiency spectral efficiency tradeoff of zero-forcing detector in massive MIMO systems[J].IEEE Transactions on Communications，2014，62(11)：3874-3890.

[11] CUI S，GOLDSMITH A J，BAHAI A.Energy-efficiency of MIMO and cooperative MIMO techniques in sensor networks[J].IEEE Journal on Selected Areas in Communications，2006，22(6)：1089-1098.

[12] BJORNSON E，SANGUINETTI L，HOYDIS J，et al.Designing multi-user MIMO for energy efficiency：When is massive MIMO the answer?[C].2014 IEEE Wireless Communications and Networking Conference(WCNC).IEEE，2014：242-247.

[13] NGO H Q，LARSSON E G，MARZETTA T L.Energy and spectral efficiency of very large multiuser MIMO systems[J].Communications IEEE Transactions on，2011，61(4)：1436-1449.

作者信息：

吴君钦，彭  斌

（江西理工大学 信息工程学院，江西 赣州341000）