0 引言

    单载波频域均衡(SC-FDE)技术^[1]，由于其在对抗多径引起的时间弥散效应中的优异性能，近些年引起了研究者的广泛关注。相对于正交频分复用(OFDM)，SC-FDE拥有更低的均峰比，使得其成为了LTE中的上行链路技术。

    置信传播算法(BP)，也称和积算法^[2]，是一种广泛应用于迭代接收机的消息传递方法。由于其在离散信号处理下的优异性能，使得BP算法在无线接收机设计中得到广泛应用。但是BP算法在连续和离散共存的场景中会导致极高复杂度，所以出现了几种近似消息传递方法^[3-5]，在有些场景下替代BP算法。有常见的两种理论化的 (Theorized)消息传递方法：平均场(MF)算法^[3]、期望传播(EP)算法^[4]。其中，平均场(MF)算法适合用于因子节点为指数类分布的场景，特别适用于高斯函数或者伽马函数的情形，但是由于其更新规则的特点，在遇到“乘积-求和”(summation-multiplication)模型时，会产生方差丢失问题，导致性能严重下降^[6]。期望传播(EP)算法^[4]可以看作是BP方法的一种近似，方便解决BP算法在连续-离散共存情况下的复杂度过高问题。但是由于MF、EP都是BP算法在放宽约束条件下的近似，所以相比BP算法均会使得性能下降。所以近年来联合BP-MF^[5]、联合BP-EP等方法出现解决了性能和复杂度的矛盾。

    文献[7]中提出了一种低复杂度稀疏信道估计SC-FDE接收机，其利用导频估计稀疏信道，并用于数据检测。由于其仅利用导频估计信道，并不能完全利用数据传输中隐含的信道信息，从而此接收机属于分立接收机。文献[8]中提出一种基于消息传递算法的联合OFDM接收机，在信道估计中采用MF方法。为了避免MF方法出现的方差丢失，其采用了向量形式，将标量形式方差计算转换为协方差矩阵运算，使得性能得到提升。但是由于存在矩阵求逆，其复杂度也大幅提升。文献[9]中提出了广义平均场(GMF)方法，假设信道之间相对独立，将信道分成相互独立的分组，从而在损失性能的代价下降低复杂度。

    本文结合文献[7-9]的方法，将原本存在“乘积-求和”结构的观测节点进行因子图拉伸，将此结构脱离观测节点。经过拉伸以后，观测节点仅存在“乘积”结构，从而采用MF方法时避免了方差丢失问题，同时可以方便估计噪声方差。而“求和”结构由另外一个节点采用BP方法处理，避免了方差丢失和其他近似方法所产生的性能下降。

1 系统模型

    针对一个SC-FDE传输系统^[1]，信息序列b经信道编码和交织后得到编码矢量c，再经QAM调制后得到发送数据x，在加入循环前缀(CP)后进行信道传输。在接收端，移除CP后进行离散傅里叶变换，得到：

1.1 现有因式分解以及因子图表示

    上述传输模型，若按照文献[7-9]的方式因式分解，中间变量z和h并未体现，因式分解如下：

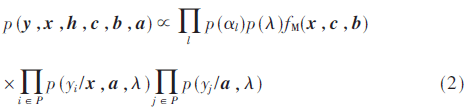
其中f_M(x，c，b)表示软输入软输出(SISO)函数，在文献[6]中有详细描述，本文不推导其内部消息更新。上述因式分解可画出因子图，如图1所示。

1.2 因子图拉伸方法

    为了避免上节中出现的复杂度与性能的矛盾，本节将系统中未知变量、观测变量和辅助变量的联合全局概率分布因式分解为：

    经过因子图拉伸，由于观测节点仅存在“求和”，则采用MF方法即可估计噪声精度又不存在方差丢失问题，而“求和”结构由节点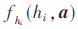表示，通过BP方法处理，保证了算法的高精度。由于避免了矩阵求逆，采用本方法后，复杂度相比向量形式的MF方法会显著下降。由于本文的因子图将中间变量z、h均通过因子图表达出来，则相比文献[7-9]本文因子图可看作是经过了“拉伸(stretched)”变换，所以本文所提方法称为拉伸因子图方法。

2 接收机设计

    基于联合BP-MF算法，本节讨论在因子图2中的消息计算。观察因子图可知，图中存在两个晶格(Lattice)状网络(f_z～x和f_h～a)，两个网络中消息更新公式类似，简洁起见本文仅详细描述频域均衡部分晶格的更新公式。

2.1 频域均衡及检测消息计算

    为了表述方便，本节将频域均衡及检测部分的消息计算分为左向消息和右向消息。

2.1.1 左向消息(f_D→f_z→f_M)

2.1.2 右向消息(f_M→f_z→f_D)

    将上节得到的消息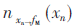传至SISO函数f_M(x，c，b)，利用BP准则进行解调解码，得到数据符号和返回的离散消息：

2.2 信道估计

    此MF消息送往信道估计部分后，利用BP更新规则更新晶格网络中的消息。同样存在晶格网络，信道估计和频域均衡部分的因子图类似，唯一的不同在于不存在SISO函数。由于和均衡部分的更新公式接近，此处不做深入探讨。利用BP方法，可以得到：

    需要说明的是，本文采用的信道估计方法也可以扩展到稀疏信道场景，采用稀疏贝叶斯学习的方法^[7-9]。只需要假设抽头先验未知，采用分层模型(2Layer或3Layer)，具体模型和因子图可参考文献[10]。

2.3 噪声精度估计

2.4 消息调度

    在信道未知情况下，若进行联合信道估计(频域数据符号z_i参与信道估计过程)，由于数据符号不准确，会导致估计准确性变差。所以本文采用的消息调度规则设定为：首先纯粹利用导频进行迭代信道估计(定义为初始化迭代)，迭代次数设定为T_init；经过初始化迭代，信道参数得到初步估计，从而可以进行频域均衡和检测；之后利用检测得到的结果再参与噪声方差估计和信道估计，从而完成全局迭代(次数设置为T_Glob)。将本节所述消息更新和调度归纳为如下算法：

3 仿真及复杂度分析

    通过蒙特卡洛仿真验证本文提出的联合信道估计迭代接收机性能，并与已知文献中算法进行对比，仿真系统参数参见表1。

    本文所提基于拉伸因子图和联合BP-MF方法标记为“BP-MF”，文献[9]中提出的分块MF方法统称为“MF”，并根据其分块大小分别记为“MF-512”、“MF-128”、“MF-32”和“MF-8”。文献[7]中采用的非联合方法，记为“DisJoint”。作为参考标准，本文也将已知信道情景进行了仿真，记为“GvChnl”。

3.1 仿真结果

    图3对比了本文以及文献中的已知方法随信噪比变换曲线(迭代次数固定为20)。从图3可看出，本文提出的BP-MF方法比MF方法在分块大小为512情况下性能有所提升。而MF方法随着分块的增加，性能逐步递减。非联合式接收机，由于仅利用导频进行信道估计，所以相比联合接收机其性能有很大劣势。

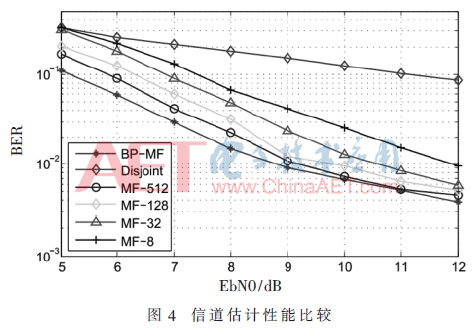
    图4展示了各种方法在不同信噪比下的信道估计性能。可以明显看出，相比非联合接收机，由于数据符号所携带的信道信息得到了利用，其信道估计性能有非常明显提升。本文所提算法相对于MF-512，有一定程度的性能优势。

3.2 复杂度分析

    分块MF方法，其复杂度随分块的变小而减小。假定分块大小为G，则其复杂度正比于O(L(M/G)²)。本文提出的BP-MF方法，计算消息个数正比于O(ML)，每条消息计算均仅需要基本的数学运算，所以BP-MF方法的复杂度正比于O(ML)。在本文仿真场景下，BP-MF方法和MF-32复杂度近似。

4 结论

    基于因子图拉伸和消息传递算法，本文提出一种低复杂度联合信道估计SC-FDE接收机。通过对现有方法的因子图进行拉伸变换，可以将图中因子节点按功能进行分割，进而采用更为灵活的消息传递算法。从而在选择消息传递规则时可以参考各种规则自身的优缺点，最大化地利用其优势，避免其缺陷。仿真结果表明，相比已有联合接收机算法，本文提出的基于因子图拉伸和联合BP-MF算法在提升性能的情况下能够显著降低复杂度。

参考文献

[1] FALCONER D，ARIYAVISITAKUL S L，BENYAMIN-SEE-YAR A，et al.Frequency domain equalization for single-carrier broadband wireless systems[J].Commu. Magazine，IEEE，2002，40(4)：58-66.

[2] KSCHISCHANG F R，FREY B J，LOELIGER H A.Factor graphs and the sum-product algorithm[J].IEEE Transactions on Information Theory，2001，47(2)：498-519.

[3] WINN J，BISHOP C M.Variational message passing[J].Journal of Machine Learning Research，2005，6(2)：661-694.

[4] MINKA T P.Expectation propagation for approximate Bayesian inference[C].Seventeenth Conference on Uncertainty in Artificial Intelligence. Morgan Kaufmann Publishers Inc. 2001：362-369.

[5] RIEGLER E，KIRKELUND G E，MANCHON C N，et al.Merging belief propagation and the mean field approximation: a free energy approach[J].IEEE Transactions on Information Theory，2012，59(1)：588-602.

[6] YUAN Z，ZHANG C，WANG Z，et al.An auxiliary vari-able-aided hybrid message passing approach to joint channel estimation and decoding for MIMO-OFDM[J].IEEE Signal Processing Letters，2017，24(1)：12-16.

[7] 王忠勇，郭秋歌，王法松，等.基于分层模型的SC-FDE系统低复杂度稀疏信道估计[J].信号处理，2015，31(9)：1106-1111.

[8] PRASAD R，MURTHY C R，RAO B D.Joint approximately sparse channel estimation and data detection in OFDM systems using sparse Bayesian learning[J].IEEE Transactions on Signal Processing，2014，62(14)：3591-3603.

[9] PEDERSEN N L，MANCHON C N，FLEURY B H.Low complexity sparse Bayesian learning for channel estimation using generalized mean field[C].European Wireless 2014，European Wireless Conference；Proceedings of.VDE，2014：1-6.

[10] ZHANG C，YUAN Z，WANG Z，et al.Low complexity sparse Bayesian learning using combined BP and MF with a stretched factor graph[J].Signal Processing，2017，131(1)：344-349.

作者信息：

袁正道1，2，王忠勇3，张传宗3，吴  胜4

（1.解放军信息工程大学 信息系统工程学院，河南 郑州450001；2.河南广播电视大学 信息工程学院，河南 郑州450008；

3.郑州大学 信息工程学院，河南 郑州450001；4.清华大学 宇航研究中心，北京100084)