0 引言

    飞机在飞行过程中不可避免会遭到雷击。据统计，飞机在每1 000～2 000飞行小时就很有可能遭遇到一次雷击^[1]。飞机防雷设计的第一步为确定飞机的雷击附着点^[2]。早在20世纪60年代，国外就开始采用飞机穿越雷暴区域的方法来获得相关雷电数据^[3]。为降低成本和风险，国外逐步采用理论分析以及模型试验的方法来对飞机雷击附着位置进行分析^[4]。根据标准SAE-ARP5416^[5]的规定，现在有3种方法来确定飞机的初始雷击附着位置：(1)全尺寸飞机进行高压雷击试验。该方法获得的结果准确，但是存在成本较高、试验周期较长的缺点；(2)采用缩比飞机模型进行试验。由于飞机周围空间电荷分布与飞机缩比比例并不成严格的线性关系。因此，该方法获得的雷击附着位置有可能与实际情况存在一定差异；(3)理论分析方法^[6]，如滚球分析法等。该方法开展起来较为简单，但是存在结果不准确的缺点。国内也有学者针对飞机初始雷击附着位置开展相关研究^[7-9]，但相关方法没有考虑雷电下行先导电荷分布的情况，与实际雷电下行先导特性不符。

    目前在对飞机初始雷击附着位置研究中采用的方法^[7-8]与实际雷电存在一定区别。因此，本文研究如何以更加贴近实际过程的方法来确定直升机初始雷击附着位置，提出一种新的雷电三维发展模型用来确定直升机初始雷击附着位置。该模型考虑LPM（Leader Progression Model）模型中下行先导电荷分布的同时，加入下行先导发展的概率参数来模拟实际雷电的曲折性，并同时考虑双向先导发展，对于直升机防雷设计具有一定意义。

1 模型建立

    在LPM中，下行先导与迎面先导满足最终击穿条件时，发生飞机遭遇雷击情况。该模型主要有3个方面的影响因素^[10]：下行先导电荷分布及发展规则、迎面先导起始判据及发展规律、最终击穿条件。

1.1 下行先导电荷分布

    由于尚无有效方法对雷电下行先导通道的电荷分布进行确定，往往采用对回击电流进行分析从而得出下行先导电荷分布。一般而言，下行先导电荷分布主要有均匀分布、线性分布^[11]、指数分布^[12]3种不同模型。由于下行先导通道内的电荷主要集中在先导头部；而在先导通道的其他部分，电荷密度则以近似线性方式向云端递减^[13]。因此，在本文对先导头部采用点电荷，而先导通道则采用线性分布的线电荷来模拟。其中，先导通道除头部以外的区域的线电荷密度分布随着高度的降低而增加，其线电荷密度可表示为^[14]：

式中：a₀为常数，其值为-1.5×10^-5；I_p为回击电流峰值，kA；H_c为雷云高度，m；h为先导所处高度，m。

    先导头部电荷采用点电荷来模拟^[15]，如图1所示。根据Gauss定理，先导头部周围流注区半径为rL与其所在高度的线电荷密度为^[14]：

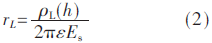
式中：E_s为流注区的平均场强，kV/m。而先导头部流注区半径为R_s内的电荷量Q_p同样可由Gauss定理得^[14]：

1.2 下行先导发展规则

    为了描述下行先导通道曲折的形态，本文利用DBM模型中的概率击穿来作为下行先导发展依据。本文采用DBM模型中的WZ模型的发展概率来进行作为下行先导发展规则，并且只对下行先导主通道进行模拟而忽略闪电分支。先导发展到第i步时各个点的发展概率P_i为：

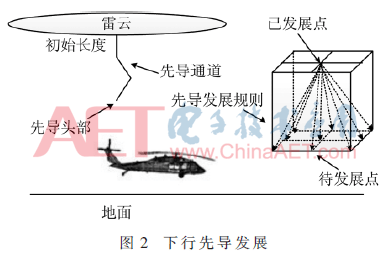
1.3 上行先导起始判据及发展规律

    飞机遭遇雷击的情况包括飞机截断自然雷电先导以及飞机自身触发的闪电^[5]。本文主要分析飞机截断自然雷电先导的情况，随着负极性下行雷电先导不断靠近飞机，在飞机端部产生的放电现象会发展成为正极性先导。在外部电场的驱使下，下行负极性雷电先导最终与飞机产生的正极性先导相连，从而发生飞机截断自然雷电先导的情况。一开始飞机端部产生正极性先导的位置便成为了初始雷击附着位置。因此，飞机端部正极性上行先导起始判据成为了判断飞机初始雷击附着位置最主要的因素。

    根据Dellera^[16]的研究成果，当迎面先导初始阶段上、下行先导之间的发展速度比约为1：4，而当上、下行先导之间的空气临近击穿时，速度比为1：1。本文取上、下行先导发展速度比为1：4，同时忽略不同阶段上、下行先导发展速度比的变化。同时，认为迎面先导始终朝着其头部电场强度最大的方向发展。

    当迎面先导头部与雷电下行先导头部之间的电场强度平均值达到500 kV/m^[17]时，认为先导头部之间的流注区相遇，从而空气间隙被击穿，发生飞机遭遇雷击的情况。

2 仿真环境

2.1 实验方法简介与仿真设置

    根据标准^[5]中对开展飞机截断自然雷电先导试验方法的要求，将平板电极设置在以飞机中心为球心的球面上，由于飞机具有不严格意义上的对称性，故只需在经度、纬度上分别以30°为增量设置37个不同的电极位置，即可模拟飞机的不同飞行姿态。

    仿真过程中采用UH-60“黑鹰”直升机的等比例简化模型，其尺寸为20 m×15 m×5 m。雷电下行先导发展的长度可达数千米^[17]。如果在仿真中完整模拟出雷电下行先导通道，则会产生巨大的计算量。并且，实际上只有当下行先导较为接近直升机时，直升机端部位置表面电场强度才会满足迎面先导的产生条件。因此，仿真中实际只仿真雷电下行先导接近直升机时的情况，并且参考标准^[5]中对飞机进行雷击附着点试验的规定对仿真环境进行设置。根据标准^[5]的规定：(1)试验过程中所用的平板尺寸应大于飞机最大尺寸的3倍，而该型直升机最大尺寸达到了20 m，同时为了减少边界边缘电场对直升机所处位置电场的影响，将代表雷云的上边界以及代表地面的下边界尺寸设为100 m×100 m；(2)代表雷云的平板电极离飞机的距离应大于50 m，代表地面的下平板离飞机距离应大于飞机最大尺寸。由于随着飞机姿态的变化，飞机离上、下极板的距离也相应会发生变化，同时考虑到下行先导的发展，因此，将飞机离上极板的距离增加到70 m，离下极板的距离增加到30 m。

    在负极性地闪过程中，雷云主要起到在云地之间建立稳定的电场环境以及给下行梯级先导提供电荷的作用，并且在下行先导中的电荷远远小于雷云中的电荷数。因此，雷云中的电荷量可以近似为固定值，雷云在云、地之间维持的电场强度也相对稳定。在仿真中将代表雷云的上极板电势设置-2 MV来保证仿真区域背景场强能达到-20 kV/m^[18]，将代表地面的下极板电势设置为0，仿真环境如图3所示。

2.2 仿真流程

    仿真中，雷电先导按照前文所述下行先导发展过程进行仿真。每进行一步仿真，由COMSOL对空间电场重新计算，采用式(4)和式(5)依概率对下一待击穿点进行选择，以确定下一步下行先导的发展路径。同时，对直升机表面电场强度进行分析，如果其表面电场强度大于临界电场强度，则该点满足产生迎面先导条件，开始发展由飞机产生的迎面先导，仿真流程为：

    (1)对仿真环境进行初始化；

    (2)采用式(5)和式(6)计算下一步先导待发展点的发展概率，并利用Monte-Carlo法对待发展点进行选择；

    (3)对直升机各位置表面场强进行分析，如果没有超过临界场强，则进行步骤(4)；如果该位置场强达到临界电场强度，则该位置满足产生迎面先导的条件，跳到步骤(5)；

    (4)按照式(1)和式(4)分别对已发展的先导通道和先导头部电荷进行赋值，并且重新计算空间场强，回到步骤(3)；

    (5)按照前文所述迎面先导发展规律，分别进行下行先导以及迎面先导的发展。如果下行先导与迎面先导之间的电场强度平均值达到500 kV/m，则认为满足最终击穿条件，整个仿真过程结束。

3 仿真结果分析

3.1 空间电势分布

    本文采用的下行先导电荷主要集中在先导头部位置，导致在先导头部附近电势较强。并且下行先导通道随着高度增加，先导通道电势随之降低。在下行先导通道不断靠近直升机的过程中，直升机机体良好的导电性使其为等势体的状态，并与外部环境电势保持一致。直升机外部空间电势分布如图4所示。

3.2 下行先导通道

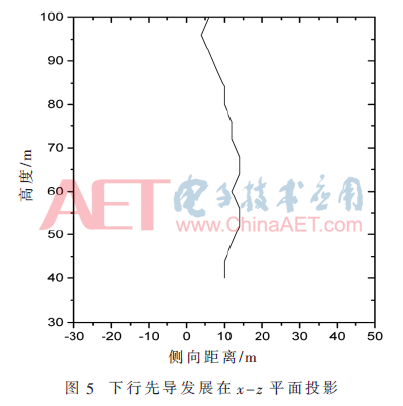
    本文下行先导发展路径采用的是概率击穿模型，先导发展具有一定随机性。如图5所示为下行先导在x-y平面的投影。由图5可以看出，下行先导在x轴偏移的距离并不是很大，最大偏移量为7 m。

3.3 雷击附着位置

    为了简化计算、揭示规律，以平板电极位于直升机最上方位置时为例，对该型直升机闪电附着位置模拟。选取直升机表面易遭雷电附着的端部进行分析，选取的端部位置如图6所示。总共进行10次下行先导发展仿真，分别记录直升机尾旋翼翼尖、主旋翼翼尖、水平尾翼以及机头部位遭受产生迎面先导的次数，如表1所示。

    由表1仿真结果可以看出，当平板电极位于直升机最上方位置时，在10次的仿真中，主旋翼B位置产生了6次迎面先导，即表明主旋翼B位置最易遭受雷电附着。而主旋翼C和主旋翼D位置产生迎面先导的次数相等，均为1次，即表明其遭受雷电附着的可能性相等。图7为当下行先导接近直升机时，在主旋翼A位置产生迎面上行先导。

4 结论

    本文将LPM模型与WZ模型相结合，实现了对雷电先导放电的三维数值模拟，并成功利用该方法来确定直升机初始雷击附着位置。主要成果如下：

    (1)对LPM模型中下行先导电荷分布及发展规则、迎面先导起始判据及发展规律、最终击穿条件等进行了分析推导，采用WZ模型中的概率击穿模式作为下行负极性先导的发展依据，并考虑上、下行先导双向发展模式，提出了一种基于分形先导发展理论的直升机初始雷击附着判别方法。

    (2)由于直升机机体模型的复杂性，很难采用编程的方式对其进行描述。本文采用COMSOL Multiphysics 4.4将复杂的直升机模型转化为MATLAB语言，并采用MATLAB编程的方式将提出的雷电发展模型运用于确定直升机初始雷击附着位置中。

    (3)为了简化计算、揭示规律，本文仅分析了当平板电极位于直升机正上方时，直升机遭遇雷电附着的情况。从仿真的结果可得：主旋翼翼尖遭遇雷电附着的可能性很大。实际中，直升机相对巨大的主旋翼会对下方机体部分产生屏蔽效应，从而导致主旋翼遭遇雷电附着的可能性比机体其他部位要大。

参考文献

[1] SAE.ARP5412B.Aircraft lightning environment and related test waveforms[S].Warrendale，PA：Society of Automotive Engineers，2013.

[2] 黄立洋，陈晓宁，郭飞，等.直升机雷电间接效应数值仿真[J].强激光与粒子束，2015，27(8)：083205. 

[3] FITZGERALD D R.Probable aircraft “triggering” of lightning in certain thunderstorms[J].Mon Weather Rev，1967，95：835-842.

[4] LALANDE P，BOUNDIOU C A，LAROCHE P.Computation of the initial discharge initiation zones on aircraft or helicopter[C].Proceedings of the 1999 International Conference on Lightning and Static Electricity.Toulouse，June 22-24，1999.

[5] SAE.ARP5416A.Aircraft lightning test methods[S].Warrendale，PA：Society of Automotive Engineers，2013.

[6] JONES C C R.International aerospace and ground conference on lightning and statics electricity[C].Bath，UK，September 25-28，1989.

[7] 陈晓宁，黄立洋，郭飞，等.直升机初始雷击附着区域划分仿真研究[J].电波科学学报，2015，30(5)：976-983.

[8] 孙柯岩，赵小莹，张功磊，等.基于分形理论的飞机雷击初始附着点的数值模拟[J].物理学报，2014，63(2)：029204.

[9] 赵玉龙，刘光斌，余志勇.飞行器雷击附着点数值仿真研究[J].微波学报，2012，28(4)：39-42.

[10] 曾嵘，耿屹楠，李雨，等.高压输电线路先导发展绕击分析模型研究[J].高电压技术，2008，34(10)：2041-2046.

[11] ERIKSSON A J.The lightning ground flash-an engineering study[D].Ph.D.thesis，Faculty of Engineering University of Natal，Pretoria，South Africa，1979.

[12] GLODE R H.The frequency of occurrence and their distribution of lightning flashes to transmission lines[J].AIEE Transactions，1945，64：901-910.

[13] COORAY V，RAKOV V，THEETHAYI N.The lightning strike distance-revisited[J].Journal of Electrostatics，2007，65(5)：296-306.

[14] 谢施君.负极性地闪雷击点选择过程的模拟试验及仿真模型研究[D].武汉：华中科技大学，2013.

[15] He Jinliang，Tu Youping，Zeng Rong，et al.Numerical analysis model for shielding failure of transmission line under lightning stroke[J].IEEE Transactions on Power Delivery，2005，20(2)：815-822.

[16] DELLERA L，GARBAGNATI E.Lightning strike simulation by means of the leader progression mode，Patr 2：Exposure and shielding failure evaluation of overhead lines with assessment of application of application graphs[J].IEEE Transactions on Power Delivery，1990，5(4)：2023-2029.

[17] DWYER J R，UMAN M A.The physic of lightning[J].Physics Reports，2014，534：147-241.

[18] Xu Yazhong，Chen Mingli.A 3-D self-organized leader propagation model and its engineering approximation for lightning protection analysis[J].IEEE Transactions on Power Delivery，2013，28(4)：2342-2355.

作者信息：

顾超超1，陈晓宁1，黄立洋2，林  楚1，王淑敏1

（1.解放军理工大学 国防工程学院，江苏 南京210007；

2.解放军理工大学 电磁环境与电光工程国家级重点实验室，江苏 南京210007）