文献标识码: A
DOI:10.16157/j.issn.0258-7998.166289
中文引用格式: 李校林,李银,何强. 一种改进的航拍图像序列自动排序算法[J].电子技术应用,2017,43(9):137-140.
英文引用格式: Li Xiaolin,Li Yin,He Qiang. An improved automatic sorting algorithm for aerial image sequences[J].Application of Electronic Technique,2017,43(9):137-140.
0 引言
近年来,由于无人机航拍具有高灵活性、高效率以及低成本的优势,已经被广泛应用于自然灾害评估、战场侦察、环境监测等领域[1-2]。为了扩大视野、全面了解和分析拍摄信息,有效的图像拼接技术非常重要。通过无人机遥感平台获得的图像具有数据量大、相位振幅小、重叠度高等特点,在后期处理图像时很容易混乱图像序列的次序,这样会给后续的图像配准和融合带来一定的困扰,不能达到理想的拼接效果。而目前很多的拼接涉及的算法[3-4]都要求人为地将图像序列排好才能进行有效的拼接,这样的人工设定是非常耗时的,特别是对航拍图像数据来说,不能满足实时性的要求。
利用计算机来完成图像序列的自动排序技术已经被提出,并且得到广泛的研究[5-9]。文献[6]提出了一种利用等距离匹配的思路来实现图像序列的自动排序,该方法不仅计算量大,对各种干扰环境的鲁棒性也较差。文献[7]利用相位相关法来实现图像序列的自动排序,该方法具有一定的抗干扰能力,但是需要人工选定阈值,算法的适应和自动性明显降低。文献[8]利用相位相关法图像间的相关性来判别位置关系,但是要求序列图像的大小必须相同,且图像的位置关系的确定说明的不够明了。文献[9]利用尾部补零的方法使图像大小相同,再运用相位相关法排序图像,但该方法在增加了算法复杂度的同时,又没有考虑旋转因素的影响。本文在总结相位相关法的基础上,针对无人机获取的遥感图像存在平移、旋转、尺度缩放的情形,提出了利用对数极坐标的方式来表示图像间的关系,建立图像序列排序模型并通过公式推导验证,突破了图像大小相同的限制,增强了算法的适用范围。
1 相位相关法原理
相位相关方法是基于二维傅里叶变换的特性,即空域平移相当于频域。1975年,KUGLIN C和HINES D[10]发现相位相关方法与场景无关,可以准确地在良好条件下对二维平移图像进行对齐。相位相关法通过利用傅里叶变化变换得到互功率谱的相位信息,其对图像的灰度信息依赖性较小,因此具有一定的抗干扰能力,设计流程图如图1。
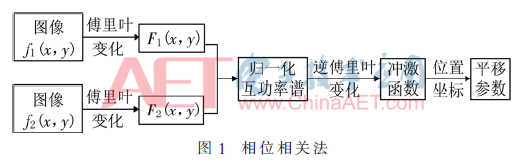
相位相关法原理可描述为:
设两幅图像A(x,y)和B(x,y),它们之前仅存在着平移关系,相对水平、垂直平移量为x0、y0,则有:

在空间域中找出式(4)中冲击函数对应的峰值位置,其值反映了两幅图像的相关性,同时确定平移参数(x0,y0)。当图像间有噪音、复杂透视,甚至存在运动物体时,冲击函数的能量会从单一峰值分布到其他小峰值上,但是最大峰值所在的位置仍然具有一定的稳定性,保证了平移量的不变性。
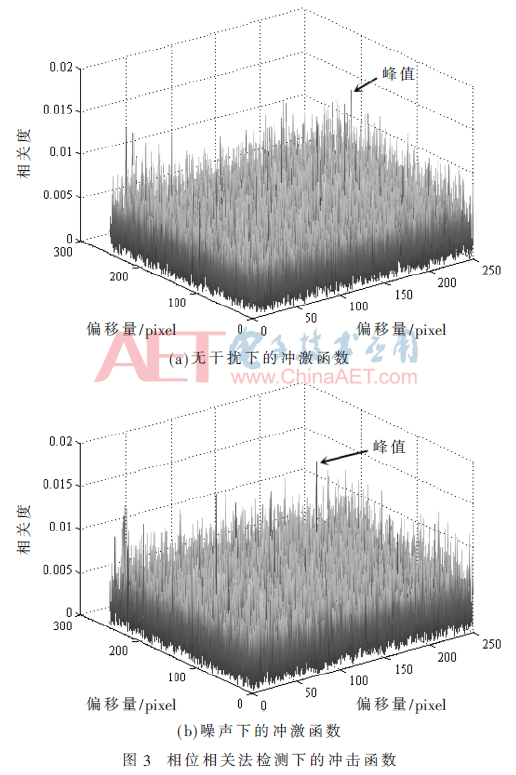
图2(a)和图2(b)是具有重叠区域的低空航拍图像,大小为500×750,图2(c)和图2(d)分别为图2(a)、图2(b)加入高斯噪声(均值为0、方差为10)后对应的灰度图像。图3(a)是图2(a)、图2(b)运用相位相关法在空间域中检测到的冲击函数δ,图3(b)是图2(c)、图2(d)运用相位相关法在空间域中检测到的冲击函数δ。从图3中可以看出,利用相位相关法检测到的δ峰值点对噪声具有一定的抗干扰能力,并且可以计算水平量(124,23),表示图2(b)相对于图2(a)右移124 pixel,上移为23 pixel。

2 改进相位相关算法方案
上节介绍经典的相位相关法严格要求待排序的图像尺寸大小相同,通过对互功率谱进行逆傅里叶变换得到的归一化相关系数是一个与f1(x,y)、f2(x,y)大小相同的矩阵,所以存在左右平移的混淆问题。同时,对于从传感器中提取出来的航拍图像,不仅包含平移、旋转,还极大可能存在尺度缩放的情况。本文提出对数极坐标的方式来表示两幅待匹配图像的关系,建立了旋转、平移、尺度变换的排序模型,增强了算法的适用范围。
原理描述:定义两幅待拼接图像间的平移参量x0、y0,旋转角度α,缩放因子σ,则f1(x,y)和f2(x,y)的位置关系可表示为:

式(10)转化成了同式(1)简单平移类似的形式,采用上节普通的相位相关法可以计算出旋转角度α=α0。
(2)当确定下来旋转角度α0时,同样代入式(9)中得:
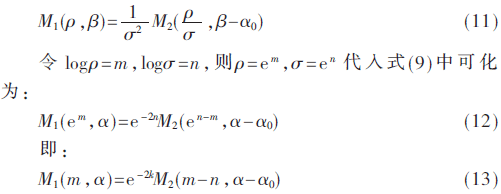
同样,式(13)化为与式(1)类似的形式,运用普通的相位相关法可以计算出n和旋转因子σ。
至此把计算出的旋转角度α0和缩放因子σ0代回到式(5)中,再次运用相位相关法就可以计算出平移参数。
根据上述原理可设计改进相位相关算法方案流程图,如图4。

3 序列图像的自动排序算法
假设有N幅待拼接的图像,根据改进的相位相关算法方案,设计以下自动排序算法:
(1)构建二维最大相关度数组。对每一幅图像根据上节提出的相位相关算法计算与其他图像的归一化互功率谱,并求得其逆傅里叶变换的峰值作为图像间的相关度,这样每一幅图像可到N-1个相关度,从而建立N×N的二维数组用来存储图像间的相关度。
(2)确定头图像和尾图像。对于每一幅至少会与其中一幅图像相邻(头图像和尾图像),最多会与其中两幅图像相邻(中间图像)。而两幅相邻的图像,其δ脉冲函数在空间域中对应着非常尖锐的峰值,即为最大相关度,根据该峰值就可以计算出两幅图像间的平移参量。因此按照每一幅图像数列的行、列找出2个最大相关度,可以得到2N个最大的相关度。而对于头、尾两幅图像仅与一幅图像相邻,其最大相关度明显大于其他相关度,则其对应的图像即为头图像和尾图像。如果该图像的最大相关度对应的水平平移量Δx<0,则其为头图像;反之,为尾头像。
(3)确定相邻两幅图像的左右关系。顺着头图像根据最大相关度对应的平移量可依次确定整个图像链,如果x0>0,则图像应该排在右边,反之排在左边。
由此得到的序列图像对应于相机由左向右拍摄的结果。
4 实验结果与分析
通过无人机自动拍摄获得的视频序列图像,从每30帧的视频序列中提取1帧用于拼接,从实验中使用的150帧中选择5帧,初始空间图像方向角度为60°,初始接触中心点为图像的中心点。5个重叠无序的UAV图像序列如图5所示,其中有323×370、224×256、313×302 3种大小类型的图像,并且这些图像之间存在着明显的平移、旋转和缩放,运用上述提出的相位相关法计算出两两图像间的相关度,统计数据如表1,根据最大相关度可优先确定头图像和尾图像(在表中用*标出);同时计算出每幅图像最大相关度的相关图像之间的水平平移量,如表2,根据平移量的大小可确定两幅图像的左右关系,从而完成实验图像序列的自动排序排序,排序后的图像序列如图6。从实验结果上可以看出,本文提出的相位相关算法不仅避免了人工设定阈值以及左右图像混淆问题,同时克服了对序列图像大小一致的限制,增强了算法的适用范围。由于算法在频域中计算相关度时耗时较大,可借助FFT的方法。并且改进后的算法可直接得出图像间的平移参数,这对图像拼接的后续的关键技术具有很大研究价值。




5 结论
本文根据航拍图像的特征提出了一种改进的相位相关算法方案,实现了序列图像的自动排序。主要采用对数极坐标的方式表示图像间平移、旋转、缩放的复杂关系,突破了已有算法对图像尺寸的限制,并给出了算法实现的具体方案。通过最大相关度的确定序列头、尾图像,再利用峰值所在坐标确定平移参数,根据给定的准则判断图像左右位置关系,避免了人工干预。实验证明,该算法能够快速有效地完成航拍图像序列的自动排序,为全景图像拼接奠定了一定的基础。
参考文献
[1] Wu Bin,Yang Jian.A method of obtaining accurate active area of remote sensing image and application in mosaicking[C].Remote Sensing, Environment and Transportation Engineering(RSETE),2012 2nd International Conference,2012:1-4.
[2] 徐丽艳.基于特征点的遥感图像配准方法及应用研究[D].南京:南京理工大学,2012.
[3] LOWE D G.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision,2004,60(2):91-110.
[4] BAY H,ESS A,TUYTELAARS T,et al.Speeded up robust features(SURF)[J].Computer Vision & Image Understanding,2008,110(3):346-359.
[5] SONG R,SZYMANSKI J.Auto-sorting scheme for image ordering application in image mosaicing[J].Electronics Letters,2008,44(13):798-799.
[6] 华顺刚,曾令宜,欧宗瑛.一种快速的柱面全景图像拼接算法[J].数据采集与处理,2006(4):434-438.
[7] 赵辉,陈辉,于泓.一种改进的全景图自动拼接算法[J].中国图象图形学报,2007(2):336-342.
[8] 赵万金,龚声蓉,刘全,等.一种用于图像拼接的图像序列自动排序算法[J].中国图象图形学报,2007(10):1861-1864.
[9] 吴宪祥,郭宝龙,王娟.一种改进的序列图像自动排序算法[J].光电子·激光,2009(8):1114-1117.
[10] KUGLIN C,HINES D.The phase correlation image alignment method[C].Conference on Cybernetics and Society,1975:163-165.
作者信息:
李校林1,2,李 银1,何 强1
(1.重庆邮电大学 通信新技术应用研究中心,重庆400065;2.重庆信科设计有限公司,重庆400065)

