文献标识码: A
DOI:10.16157/j.issn.0258-7998.171107
中文引用格式: 沈思博,万秋华,杜颖财,等. 高精度光电编码器信号补偿技术的研究进展[J].电子技术应用,2017,43(10):26-30.
英文引用格式: Shen Sibo,Wan Qiuhua,Du Yingcai,et al. Development of signal compensation technology for high-precision photoelectric encoder[J].Application of Electronic Technique,2017,43(10):26-30.
0 引言
在各种电机控制系统中,可靠的位置反馈信息对于系统的控制起着至关重要的作用,光电轴角编码器是当前最重要的位置反馈信息获取方案[1],主要用于测量转子的角位置和转速。和传统角度测量装置相比,光电轴角编码器不但能够达到更高的分辨力和精度,还具有高频响以及体积小、重量轻、结构简单、可实现数字量输出等多项技术优势。高精度的光电编码器满足高精尖领域对于测量的精度和速度的超高要求,广泛应用于航空航天、精密仪器仪表、自动化控制等各个领域[2-3]。
光电编码器是一种根据莫尔条纹原理研制的角位置传感器。光电接收元件(如光敏二极管)接收通过重叠的狭缝和码盘的莫尔条纹光信号,当编码器旋转时,获得一个接近正弦信号的电信号;通过安装另一不同角度的狭缝,获得一个与正弦信号相位差为π/2的余弦信号,理想信号如式(1)所示:

对比分析式(1)与式(2),实际信号相较于理想信号存在以下四种影响信号质量的主要误差:直流电平漂移、等幅性偏差、正交性偏差和高次谐波。其中以等幅性偏差和正交性偏差对信号的影响最大,因此对编码器实际光电信号的补偿主要是针对此两种误差[4]。本文从这四项典型的细分误差角度出发,系统地总结了现有的光电编码器信号补偿方法,分析了现有方法的优点和存在的限制,讨论了随着光电编码器理论和实践的不断创新,光电信号补偿技术的发展趋势和研究方向。
1 直流电平漂移、等幅性偏差补偿
对莫尔条纹光电信号直流电平漂移、等幅性偏差的补偿主要是通过硬件电路补偿法,并朝着自动化方向不断改进。
1.1 硬件补偿法
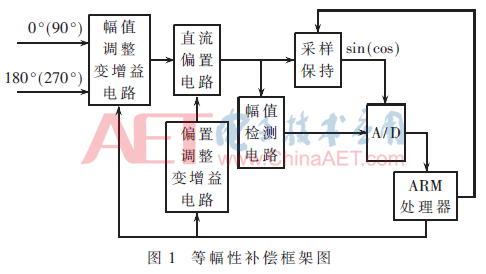
早期对于信号的直流电平漂移与等幅性偏差,采用人工手动调节电位计的方法进行补偿。为了实现信号的实时自适应补偿,近年来,研制了使用数字电位计的补偿电路[5]。图1为长春光机所设计的等幅性偏差补偿的框架图,采用ARM处理器接收幅值检测电路传输的幅值信号,然后与理想幅值信号比较,再通过调节幅值调整变增益电路、偏置调整变增益电路中的数字电位计调整信号的幅值和偏置。
1.2 光学补偿法
长春光机所提出在光栅上增加全透光通道的方法补偿直流电平偏差,该方法将经过全透光通道的信号反相偏置后补偿给正余弦信号,抵消了绝大部分的直流电平偏差。
1.3 软件补偿法
Jong-Joo Moon提出了依赖于编码器输出信号的lissajou图的补偿方法[6],通过计算lissajou圆在四个象限的面积和半径估计幅值误差和直流偏移误差,对此二项误差进行校正,并显示相位误差对圆面积和半径的影响。
2 正交性偏差补偿
正交性偏差是影响细分的主要偏差,现有的对正交性偏差的补偿方法主要包括光学补偿、软件补偿和硬件补偿。
2.1 光学补偿法
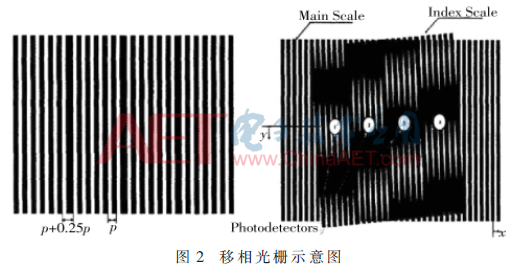
光学补偿的方法主要是通过改良光电编码器码盘和狭缝上的光栅刻划方式,达到减小细分误差的目的。韩国LG公司设计的移相光栅能够直接避免正交性偏差的产生[7]。图2为移相光栅和移相光栅与狭缝叠加所得莫尔条纹示意图。如图2所示在移相光栅的1/4、1/2、3/4处分别有3个较其他黑线粗1/4的黑线,这种光栅结构使得所获得的莫尔条纹呈阶梯式分布,相邻阶梯的莫尔条纹保持一个π/2的相位差。由此所获得的正余弦信号避免了因码盘或狭缝光栅倾斜而产生相位误差,但此方法不能避免因光源光线入射角、光电信号参数调整等其他原因引起的正交性偏差。
2.2 软件补偿方法
空军第一航空学院吕孟军为减小莫尔条纹信号不正交时的正切法细分误差,提出了一种可对任意相位滞后误差进行实时补偿的算法[8]。通过对正弦和余弦信号过零点的准确采样,计算出余弦信号与正弦信号相位差,进而确定了实际的相位计算公式。相位差测量原理如图3所示。该算法可实现对任意大小相位滞后误差的实时补偿 ,具有细分脉冲均匀、信号峰值处灵敏度高、不需要准确清楚的信号幅值等优点,但算法的实现需要额外的脉冲源产生计数脉冲,且对采样位数和技术脉冲频率有较高的要求。

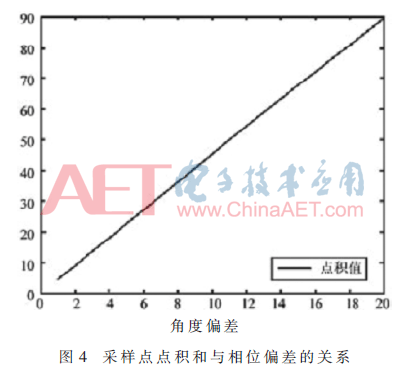
长春光机所吕恒毅提出傅里叶变换测量法和相关函数测量法两种正交性偏差测量方法[9]。傅里叶变换测量法通过对莫尔条纹光电信号进行短时离散傅里叶变换获得信号的相位差信息。相关函数测量法求取莫尔条纹光电信号的相关函数,然后由相关函数公式求得正交性偏差角。傅里叶变换测量法和相关函数测量法需要采集多个周期的信号进行运算,无法实现对信号的实时补偿,且计算要求信号频率不变即编码器转速均匀。罗刚等人运用锁相倍频电路获取莫尔条纹光电信号的正交性偏差[5]。该方法通过锁相倍频电路实现对两路光电信号的细分和整周期采样。如图4所示,根据在非正交情况下两路光电信号即正弦信号和余弦信号整周期内积和与正交性偏差成线性关系, 可以通过计算正余弦信号整周期内积推导出光电信号的正交性偏差,此方法实现了对正交性相位偏差的动态测量,但无法对信号进行实时测量且要求信号频率不能过高,频率变化不能过快。高旭等人采用了基于Hilbert 变换的运算法对莫尔条纹光电信号正交性偏差进行实时测量[10]。该方法利用Hilbert 变换的相位平移特性获得两路编码器精码光电信号的90°相位平移信号,由原信号和平移信号共同推导出两路精码光电信号的正交性偏差。所设计的补偿系统通过细分补偿查找表对信号进行补偿,采用光电信号正交性误差补偿与细分补偿查找表更新同步进行的处理方式,该方法实现了在信号频率变化情况下对正交性偏差的实时测量和对精码光电信号的自适应补偿,但此算法在运算过程中需要进行快速傅立叶变换(FFT)和反变换(IFFT),运算量大,输出延迟高,无法实现快速补偿。
从信号自身的三角函数特性出发,A. Khattab 提出了一种通过采集一个周期内三组不同的正余弦值进行三角函数计算,获得正交性偏差值,并进行在线补偿的方法[11]。该方法耗能低,易于实现,但是对于通过根号运算获得的中间值的正负判断复杂,方法不具有完备性。
2.3 硬件补偿法
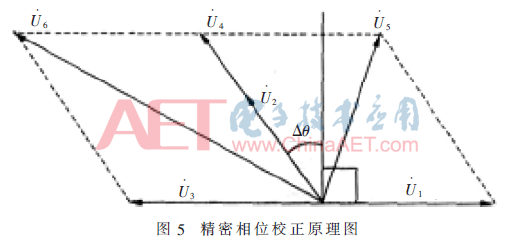
长春光机所熊文卓等人运用矢量的概念表示信号,以正弦信号为基准信号,将余弦信号分解为0°和90°两个正交分量,通过示波器观察lissajou图并调节处理电路中的机械电位器和放大器,进而消除0°分量的正交性误差[12]。为进一步减小细分误差,通过精密调节, 使余弦信号的幅值与正弦信号严格相等,将正弦及其反相信号与余弦信号分别相量相加可得到严格正交的两个新相量,从而消除正交性误差,图5为精密相位校正原理图。经精密相位校正后,正交性偏差从1″降低到0.1″左右。该方法要求对电位器进行手动调节,无法实现自动补偿,且调节精度有限。
3 高次谐波补偿
对信号所含的高次谐波的补偿方法主要分为光学补偿和软件补偿两种。
3.1 光学补偿法
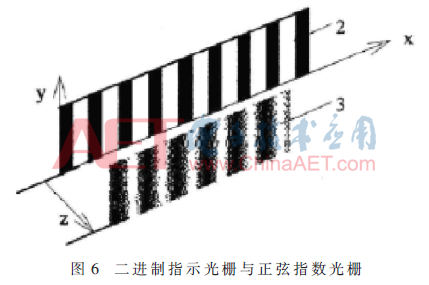
摒弃传统的二进制指示光栅,天津大学设计的正弦指数光栅可以直接滤除光场中的高次谐波[13],光栅结构如图6示。光电二极管转换经过正弦指数光栅的莫尔条纹光信号,得到的电信号模型如式(3)所示:

式中,u1=sinθ,u2=cosθ,α为正交性偏差,G为等幅性偏差,p、q为两路信号的直流电平漂移,与式(2)中经过传统光栅获得的信号比较,可以看出正弦指数光栅可以滤除信号中的高次谐波项。
3.2 软件补偿方法
哈尔滨工业大学刘杨等人提出一种莫尔条纹信号正弦性偏差的经验模态分解(Empicical Mode Decomposition,EMD)修正方法[14]。利用码盘精、粗码道刻线关系计算精码基频,运用 EMD 分解理论提取基波分量,仿真补偿正弦性偏差。
长春光机所高旭等人设计了一种基于粒子群优化算法的莫尔条纹信号正弦性偏差自动补偿方法[10],该方法建立了编码器光电信号波形的数学方程,提出了一种惯性权重自适应的改进粒子群优化算法,应用此算法对信号的非线性波形方程进行优化求解,辨识波形参数,利用辨识信息对光电信号进行补偿。从编码器的光电信号误差的产生原理出发,曹艳波等人研究了编码器的测角精度与轴系晃动产生的的低频谐波之间存在的固定的函数关系, 指出利用这种关系可以通过在编码器内部或在线的方式进行实时误差补偿,从而达到提高编码器测角精度的目的[15]。但是这种将轴系晃动的误差作为测角精度的补偿量以间接提高测角精度的方法,要求保证位置和时间序列的严格对应。
4 综合性补偿
上述补偿方法仅针对特定的某项细分误差,能够同时对编码器的两项以上的细分误差进行补偿的方法称为综合性补偿方法。
4.1 软件补偿方法
最早的对莫尔条纹光电信号进行补偿的方法是由Heydemann提出的,对信号的直流电平漂移、等幅性偏差、正交性偏差进行在线补偿,称为Heydemann补偿法[16]。该方法的原理是建立实际输出的莫尔条纹信号数学模型,如式(4)所示:
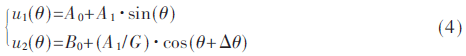
式中A0、B0表示直流电平漂移,Δθ表示正交性偏差,A1为信号的幅值,G为幅值比。然后用实际输出信号值采用最小二乘法拟合该模型,得到各项偏差值。国内有关高校提出了改良的Heydemann补偿法[17-18]。Heydemann补偿法及改良方法需要采集多个周期的数据,才能保证计算的精度。
4.2 硬件补偿法
日本日立国际电器株式会社的冈崎敬发明了“用于补偿失真的预失真放大器”,建立预失真放大器的模块单元,将放大单元、功率检测单元、失真补偿表、控制单元以及预失真单元模块化,实现对输入信号幅值、相位偏差的补偿[19]。
4.3 其他误差补偿
除了影响信号质量的短周期细分误差以外,编码器产生的原始光电信号还存在长周期误差。针对此种误差,研究了包括径向基函数网络(RBF)、傅里叶神经网络的神经网络模型[20-21]。采用理想的正弦函数训练网络,应用训练好的非线性网络模型修正非线性系统误差。
弗朗和费衍射模型较理想的正余弦模型更接近于实际输出信号,英国 Steven T.Jenkins等人提出采用弗朗和费衍射模型定义编码器输出信号的方法[22],规避了主要的细分误差源,设计并比较了开、闭环两种编码器输出信号处理系统。系统对莫尔条纹光电信号进行放大、采样、正交性偏差补偿、以弗朗和费衍射模型为参考的卡尔曼滤波,最后得到了较为理想的正余弦输出信号和角度值。但开环系统延迟较高,闭环系统虽然延迟较低,但需要额外的高速D/A转换器。
西班牙Jesus Lopez等提出了针对光电编码器振动误差的补偿方法[23],通过提前测量非振动情况下和振动情况下的编码器全周期角度值,建立全周的振动误差查找表(LUT),对在振动情况下运行的编码器光电信号使用LUT进行在线补偿。
由于空间温度的剧烈变化和光电器件的老化,严重影响编码器光电信号的强度,导致粗码译码失败和精码信号质量变差,业界人士又从器件的温度特性方面着手,开展系列补偿方案研究,如发光二极管和光电三极管配对法、热敏电阻补偿法等[24]。
5 现状分析与展望
目前对光电信号的细分误差采取的补偿方法主要分为光学补偿、软件补偿和硬件补偿三类。其中,光学补偿法只能补偿部分偏差;硬件补偿方法需要额外增加硬件电路,使得编码器可靠性下降,增加了编码器成本;软件补偿方法主要是采用基于DSP/FPGA的现代信号处理方法对光电编码器信号进行滤波或补偿,或从三角函数角度出发对信号进行处理。现有的补偿算法中,一部分算法需要获取周期性采样数据,无法实现实时自适应补偿,而且对编码器的旋转频率提出了要求,限制了编码器的应用条件;另一部分补偿算法复杂性高,运行缓慢,信号的输出延迟高。因此为了进一步提高编码器的精度,也为了满足实际工程的需要,对光电编码器信号补偿方法的研究可以从以下内容开展:
(1)快速的实时自适应信号补偿算法
为了同时提高补偿速度,又达到满足工程实际需要的精度,可以进一步研究编码器光电信号的实时自适应补偿算法。从编码器输出信号的本质出发,改进运算公式、降低运算复杂度,研究出具有高可靠性、能够快速实时补偿光电信号的补偿算法,对提高编码器精度具有重要意义。
(2)信号动态补偿方法研究
现有的补偿方法主要是针对编码器在静态测量情况下的输出信号,当用编码器动态测量位置和速度,输出信号与静态不同。已有对编码器动态误差的检测和计算方法[25-26],但对动态输出信号自动补偿方法仍需要更多研究。
(3)新型编码器信号补偿方法研究
近年来,对光电轴角编码器的需求越来越高,对编码器的性能要求越来越多样化。许多满足不同用途的编码器类型被研制出,如单圈绝对式编码器、图像编码器、光纤编码器等,由于这些编码器采用了与传统编码器不同的理论,因此其信号产生原理也与传统不同,信号所含误差也不同于以往。在研制新型编码器的过程中,对其信号误差进行分析与补偿是实现编码器更高精度的有利保障。
6 结论
本文从4项典型的细分误差指标角度出发,系统地总结了不同历史阶段,不同理论下光电编码器信号补偿方法,分析了现有方法的优点和存在的限制,指出具有针对性的高精度快速、实时补偿方法和对光电编码器动态测量情况下的信号补偿将成为工程研究的热点,同时随着各种新型编码器的诞生,相关的信号误差分析和补偿也成为不可忽视的问题。希望本文的研究能为相关领域的研究人员提供一些参考和思路。
参考文献
[1] ELLIN A,DOLSAK G.The design and application of rotary encoders[J].Sensor Review, 2008, 28 (2):150-158.
[2] 韩旭东, 徐新行, 刘长顺,等.用于星载激光通信终端的绝对式光电角度编码器[J].光学精密工程,2016,24(10):2424-2430.
[3] 赵长海,万秋华,梁立辉,等.小型高精度航天级光电编码器[J].电子测量与仪器学报,2015,29(8):1224-1230.
[4] 王显军.光电轴角编码器细分信号误差及精度分析[J].光学精密工程,2012,20(2):379-386.
[5] 罗刚,熊文卓.光电轴角编码器光电信号正交偏差的测量和补偿方法[J].传感技术学报,2008,11(21):1853-1857.
[6] MOON J J,HEO H J,IM W S,et al.Classification and compensation of amplitude imbalance and imperfect quadrature in resolver signals[J].IEEE Power Electronics and Applications,2014:1-4.
[7] SONG J H,KIM K C,KIM S H,et al.A new error compensation method in linear encoder using phase shifted grating[J].SPIE,1999,3740:124-127.
[8] 吕孟军,郭琪,吕印晓.莫尔条纹信号相位误差补偿[J].光学精密工程,2009,17(7):1694-1700.
[9] 吕恒毅,刘杨,王延东,等.莫尔条纹正交偏差的智能补偿方法[J].仪器仪表学报,2010,31(9):2075-2080.
[10] 高旭.莫尔条纹光电信号自动补偿技术研究[D].长春:中国科学院长春光学精密机械与物理研究所,2014.
[11] KHATTAB A,SALEH S,BENAMMAR M,et al.A precise converter for resolvers and sinusoidal encoders based on a novel ratiometric technique[J].IEEE,Sensors Applications Symposium(SAS),2016:1-6.
[12] 熊文卓,孔智勇,张炜.光电轴角编码器光电信号正交偏差的相量校正方法[J].光学精密工程,2007,15(11):1745-1748.
[13] Wang Chunhai,Zhang Guoxiong,Guo Shangqi,et al.Auto correction of interpolation errors in optical encoders[J].SPIE,2002,2718:439-447.
[14] 刘杨,吕恒毅,王岩,等.光通信粗瞄系统莫尔条纹信号正弦性补偿方法[J].仪器仪表学报,2012,33(8):1735-1740.
[15] 曹艳波,艾华.编码器轴系晃动对测角精度影响分析[J].光学仪器,2016,38(4):297-302.
[16] HEYDEMANN P L M.Determination and correction of quadrature fringe measurement errors in interferometers[J].Applied Optics, 1981, 20(3): 3382-3384.
[17] 王选择,郭军,谢铁帮.精密衍射光栅信号的椭圆拟合与细分校正算法[J].工具技术,2003,37(12):47-49.
[18] 徐从裕.单变量递推法莫尔条纹信号误差分离算法[J].仪器仪表学报,2013,33(8):1708-1713.
[19] JAPAN patent application EP 200610128511.7.
[20] 洪喜,续志军,杨宁.基于径向基函数网络的光电编码器误差补偿法[J].光学精密工程,2008,16(4):598-604.
[21] 冯英翘,万秋华,王树洁.小型光电编码器长周期误差的修正[J].光学精密工程,2014,22(9):2491-2497.
[22] JENKINS S T,HILKERT J M.Sin/cosine encoder interpolation methods: encoder to digital tracking converters for rate and position loop controllers[J],Proc.of SPIE, 2008,6971,69710F::1-7.
[23] LOPEZ J,ARTES M.A new methodology for vibration error compensation of optical encoders[J].Sensors.2012, 12,4918-4933.
[24] 祝成军,龙科慧.光电编码器信号自动补偿方法研究[J].测控技术,2009,28(9):6-9.
[25] 于海,万秋华,梁立辉,等.小型光电编码器动态误差检测[J].北京理工大学学报,2015,35(10):1090-1095.
[26] 左洋,龙科慧,刘金国,等.非均匀采样莫尔条纹信号的分析与处理[J].光学精密工程,2015,23(4):1146-1152.
作者信息:
沈思博1,2,万秋华1,杜颖财1,赵长海1,孙 莹1
(1.中国科学院长春光学精密机械与物理研究所,吉林 长春130033;2.中国科学院大学,北京100049)

