文献标识码: A
DOI:10.16157/j.issn.0258-7998.172194
中文引用格式: 李嘉敏,戴紫彬,王益伟. 可编程可伸缩的双域模乘加器研究与设计[J].电子技术应用,2018,44(1):28-32,36.
英文引用格式: Li Jiamin,Dai Zibin,Wang Yiwei. Research and design of dual-field programmable length-scalable modular multiplier and adder[J]. Application of Electronic Technique,2018,44(1):28-32,36.
0 引言
公钥密码体制以其独特的理论依据很好地填补了密码领域的空缺。它在密钥分发、身份认证等方面具有明显优势。1985年Neal Koblitz和Victor Miller分别独立提出了椭圆曲线在密码学中的应用。作为三大公钥密码体制之一,椭圆曲线密码体制具有相同粒度更难破解、单位比特安全强度更大的特点。
椭圆曲线密码运算在底层结构设计时,主要包括模加减、模乘和模除、模逆。其中,模除和模逆运算最为复杂,通常通过转换运算坐标来降低其实现复杂度,且使用频率不是很高。而模乘和模加减运算使用更为频繁。如何高效率、低成本地实现模乘模加减是当前的一个研究热点。1985年Montmery提出了一种全新的模乘算法,他将普通模乘的运算转换到Montgomery剩余类中进行,其所有大数均规约到了剩余类中,计算大幅度简化。Montgomery模乘算法是目前最为常见的模乘实现方法,但传统的算法具有算法粒度固定、关键运算路径过长的缺陷,而且不支持双有限域运算。文献[2]提出了一种Montgomery模乘算法在高基阵列上的优化算法。文献[3]提出了一种基于CIOS模乘的可重构可伸缩的双域模乘加器,将模乘与模加减糅合,但面积不够优化。文献[4]提出了一种改进的基于FIOS类型Montgomery双域模乘器,流水线切割较为合理。本文在前人的研究基础上,通过对双域模乘和模加减单元进行分析,以FIOS算法为基础,重新设计了一种MAS(multiplication- addition-subtraction)结构,将模乘和模加减进行可重构糅合,一定程度上降低了单元面积,又可以灵活地适配各种长度的模运算,从而适应各种不同的应用场景和任务。同时对模乘的关键运算路径进行了流水线设计,相对于传统的模乘算法,运算频率有一定的提高。
1 模乘加算法分析
模乘、模加减和模逆运算构成了ECC密码算法中的主体运算。设计模乘模加减功能复用的模乘加单元结构,可以提高结构利用率,减少多余连线资源,进而降低总体面积。本文对双域模加减算法及双域模乘算法进行了分析。根据两者运算的原理可知,模乘对模加减无论是在算法层次还是结构层次上具有较为完整的兼容性。兼容关系如图1所示。

本文针对现有模乘和模加算法进行改进,设计了如下所示的模乘加算法。
算法1 适于硬件实现的FIOS模乘加改进算法

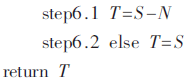
算法将输入的大整数A、B、N按照32 bit字长进行分解运算[4],字数为s,算法具有内外两层循环,对操作数按32 bit字长进行循环扫描,其中内循环完成32 bit数据的乘和64 bit的加法运算,外循环完成对被乘数的遍历扫描。算法在GF(2n)域与GF(p)域上实现过程大致相同,区别在于GF(2n)域上的加法是异或操作,乘法则为多项式乘法,并且循环结束后直接输出结果,而不需要与不可约多项式进行比较。
算法初始有一个信号a,用于判断运算模加减或者模乘。如果a=0进入step2运行模乘,否则进入step5运行模加减,而此时的加法不再是模乘中的64 bit加,而是3个64 bit加的级联,即为192 bit加。此处即为本文提出的模乘模加糅合结构的关键所在。运算过程有3个for循环,其中前两个是嵌套在一起内外循环。设计的流水运算单元也是主要用来完成这部分嵌套循环。在硬件设计过程中step2.2、2.3、2.4作为一部分结构Y。step2.5.1、2.5.2、2.5.3、2.5.4作为重复的结构X出现在硬件结构中。
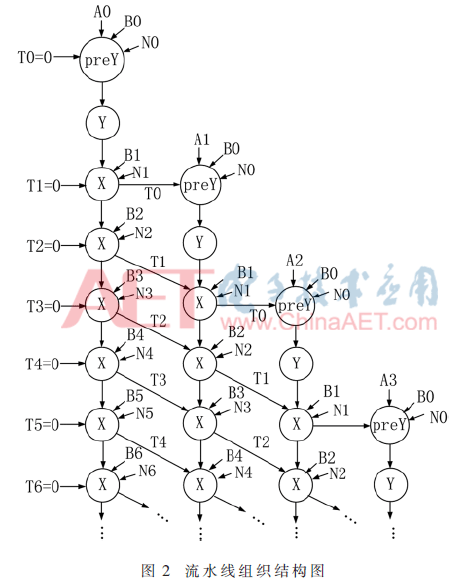
为了更加清晰描述算法中数据的传递与处理过程,列出了FIOS模乘器流水树结构,其中X与Y分别对应上文提到的结构X与结构Y(Y结构包括PreY与Y两个操作)。每一横行表示同一时钟周期参与运算的单元,每一竖列表示下一时钟周期数据传递方向。图2描述的是前n个时钟周期数据运算传递。

2 可编程FIOS模乘加器电路设计
2.1 模乘加器总体结构设计
模乘运算电路是该设计的核心,本文设计的模乘单元数据路径位宽为192 bit,通过迭代,可以完成576 bit以内任意比特的双有限域模乘运算。该模乘加数据路径核心为处理单元Y、N个处理单元X和模加减单元,其中Y结构由两部分构成,详见流水线结构设计。具体结构如图3所示。模加减单元中的两个虚线ADDER192 bit,表示其由MA X#N和MA X#N-1的相关结构替代。

双域模乘加器主要由数据输入、数据输出、状态机控制、模乘运算、模加减运算等单元构成。
数据输入输出单元负责对数据进行整合以及与外界的数据对接。其中输出单元需要根据运算域的不同改变输出模式。
状态机控制单元完成整个可重构向量模乘加单元运算时对各个模块的调度控制。根据输入的运算选择信号及数据的长度,判断进行模乘还是模加减,二元域还是素数域,以及进行模乘的轮数和。
由于算法1在实现中存在较高的内部并行性,因此模乘运算模块可以采用多个并列处理单元来组成线性阵列流水线结构实现算法提速,也就是上文提到的N个处理单元X的结构。
2.2 双域模乘加糅合部分设计
图4是模加减器结构示意图。有两个可重构的向量加法运算单元。
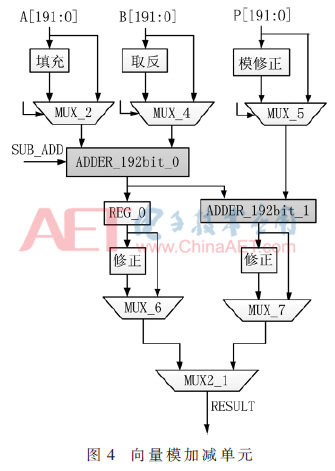
向量模加减单元的核心是一个位宽为192 bit能够进行双有限域加减法运算的加法器。当数据长度不超过192 bit时,数据路径没有反馈情况;当大于192 bit时,则在控制电路的调度下循环反馈多次运算。该192 bit加法器由6个32 bit可重构字加法器组成。其中,每个字加法器可以执行两个有限域上的加减法运算,且通过级联方式完成192 bit数据的运算,如图5所示。每个字加器无需等待上一级进位才进行运算,而是预先对两种进位情况分别进行计算,得到两种不同的结果。当前一级进位到达时,由进位信号进行结果选择。若计算数据的长度超过192 bit,则需要将第六级字加法器的进位返回至第一级字加法器,进行下一循环的计算。图6中DFA为双有限域加法器。
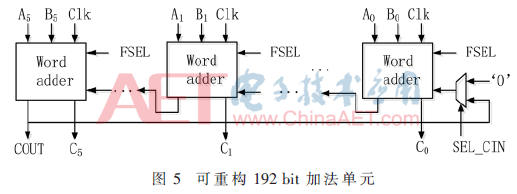

图7是模乘单元的MA X#1到MA X#N-2的结构。对应于算法的step2.6。不过,它将Tj+Ai×Bj与C+mNj并行计算,而且还有Tj-1+Ai×Bj-1与C+mNj-1进行相加的单元。

图7结构包含3个64 bit的加法器,如果进行级联,并加入进位判断电路,即可完成模加模块所需的192 bit加法运算。如图8所示,即为加入级联结构的MA X#N-1和MA X#N的结构。可以同时满足模乘与模加的运算需求。其中的ADDER64是由进位为0或1的两个32 bit加法器级联构成的,即运用了上文中可重构字加器的设计方法。

2.3 流水线单元设计
该模乘加器的流水加速设计主要体现在模乘器的嵌套循环结构上。如图9所示。该流水线单元主要由3部分构成,分别是:移存器、处理单元Y(由preY、Y构成)、处理单元X。其中,移存器完成A、B、N的字输入;Y单元完成算法中的step2.2、2.3、2.4;X单元用于完成step2.5.1、2.5.2、2.5.3、2.5.4的循环。N个X单元可以满足576 bit以内的任意比特模乘运算,以下是针对7个X的结构分析。其合理性将在后文进行分析。
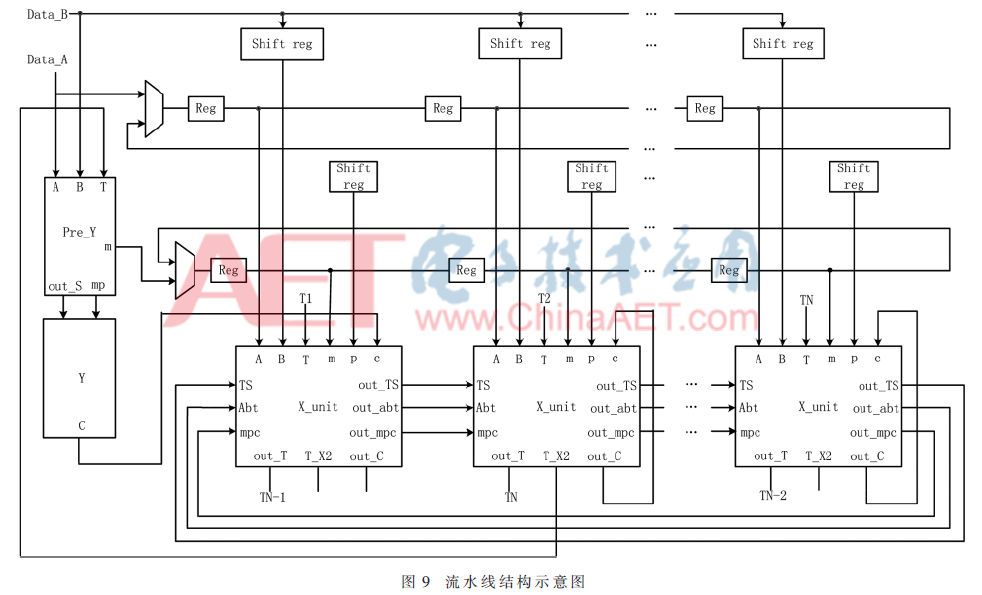
状态机产生控制信号,驱动移存期,为每个单元提供相应的数据字,数据A首先通过Y结构进行6个时钟周期的运算完成前两个字Ai与B0的乘法,而后传输到X单元中,并根据参加模乘数据的长度,进行对应轮数的X单元运算,而后以字为单位输出运算结果。下面对长度分别为192 bit、384 bit、576 bit的数据运算过程进行分析。
(1)参加模乘运算数据为192 bit时,即6个字。根据结构设计,Ai与B0在外循环中进行,X单元本级运算的数据Tj+Ai×Bj与C+mNj传到下一级使用(详见硬件结构设计),因此需要经过6个X单元的运算才能完成数据的输出。最终最低字T0在X2中输出,最高位T5在X7中输出。数据进入X单元后,需要经过两个周期才能输出。因此从第一个有效数据A1进入X1开始,第3个周期产生T0;第6个周期,第二个有效数据A2进入X1。即此时A1和B的乘法与A0和B的乘法并行运行。第12个周期,第一轮的中间T1生成,之后以此类推。
(2)参加模乘运算数据为384 bit时,即12个字。同192 bit运算,需要经过12个X单元才能完成一轮内循环。不过在X7完成运算时需要数据再次传送回X1继续进行循环,且此时恰巧Y单元没有数据输入到X1单元(Y单元每6个时钟周期更新一次Bi值。并不是每个周期都为X单元提供数据)。X单元运算需要2个时钟周期,7次运算则需要14个时钟周期。而Y单元需要6个时钟周期才会往X1中输入数据,14个时钟正介于12到18时钟周期之间,因此不会出现数据输入冲突。该结构包含7个X处理单元,可以避免576 bit以内乘法运算均不出现数据冲突。
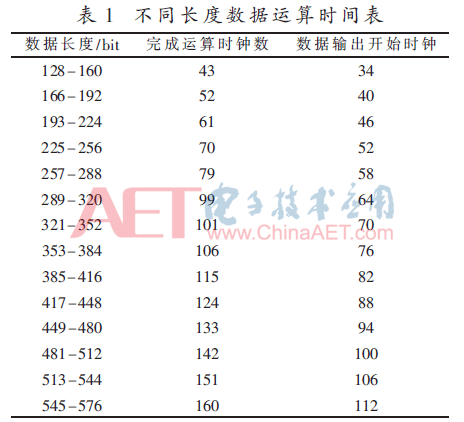
(3)参加模乘运算数据为576 bit时,即18个字。同理,需要经过18个X单元才能完成一轮内循环,要在第三轮的X4处完成第一次循环运算。而此时,7个X单元里面进行的是不同的内循环,比如第40个时钟周期(从有效数据输入Y开始计算时钟),X1到X7分别在进行A1×B14、A3×B8、A5×B2、A0×B17、A2×B11、空(X7此时无有效运算)的内循环。其中,Ai×Bj表示A的第i个字与B的第j个字相乘。对应算法step2.5.1 Hj=Tj+AiBj,Ij=mNj+C,及本轮内循环。表1是具体的运算数据表格。
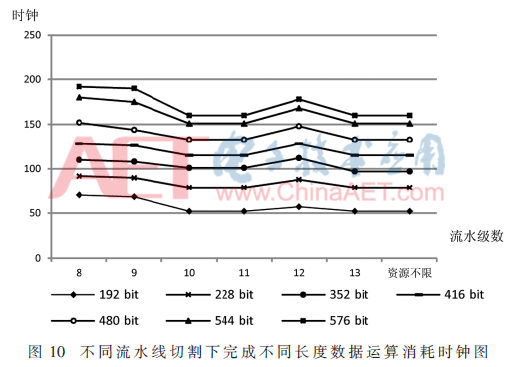
下面对不同级流水结构进行分析。图10是不同的流水线结构下完成不同长度运算用时折线图。由折线图可知,到10级流水线结构之后,再次增加X单元的数量运算周期不再降低,反而会使面积增大,降低单元的整体利用率。因此在综合了面积、运算效率及单元利用率方面因素后,最终决定采用10级流水结构,其中Y内部有三级流水,7个X对应7级。
3 性能分析
本文采用了Verilog HDL对设计进行了RTL级描述,对设计进行功能仿真验证,并在0.18 μm CMOS工艺标准单元库下对可重构模乘单元进行逻辑综合,综合工具使用Synopsys公司的Design Complier。综合结果表明,可重构模乘加单元占用面积927 312 μm2,最大延迟4.3 ns,最高时钟可达到230 MHz。由于没有同类别的可重构的模乘加单元可供比较且电路的综合环境和仿真平台不同,因此只与其他一些国内外先进设计文献中模乘器的性能进行比较。表2列出了本文与其他文献的模乘运算单元的性能比较。

由于模乘加结构的关键路径存在于模乘模块中,性能指标里面主要进行模乘方面的性能比较。与文献[3]比较,虽然速度略有差距,但是面积具有很大优势。与文献[4]比较,虽然面积略有劣势,但是支持双域运算且运算位宽范围更广。与文献[5]、文献[7]的设计相比,本文提出的结构单元在运算速度和面积方面均有优势。综合比较,本设计在功能及性能上具有较强的综合优势,并且可以适应于各种不同的场合和任务。
4 结论
本文提出了基于FIOS算法和可重构模加减算法的双域可伸缩模乘加算法。并运用了10级流水线结构,设计了支持576 bit以内的任意长度双域可重构模乘加减运算单元。在结构上很好地完成了模乘与模加减的单元公用,提高了单元的利用率。为模乘加单元的设计提供了一定的参考。
参考文献
[1] 仲先海.并行可配置ECC协处理器关键技术研究[D].郑州:信息工程大学,2008.
[2] 胡进,何德彪,陈建华.基于高基阵列乘法器的高速模乘单元设计与实现[J].计算机工程与设计,2010,31(6):1202-1204.
[3] 王威,严迎建,易卫兵.双域可重构CIOS模乘加器研究与设计[J],微电子学,2015,45(4):502-506.
[4] 杨晓辉,王雪瑞,秦帆.基于FIOS类型的Montgomery双域模乘器设计[J].电子技术应用,2011,37(10):144-149.
[5] 郭晓,蒋安平,宗宇.SM2高速双域Montgomery模乘的硬件设计[J].微电子学与计算机,2013,30(9):17-22.
[6] 史焱,吴行军.高速双有限域加密协处理器设计[J].微电子学与计算机,2005,22(5):8-12.
[7] Akashi Satoh,Kohji Takano.A scalable dual-field elliptic curve cryptographic processor[J].IEEE.Transactions on Computers, 2003,52(4):449-460.
[8] KOC C K,ACAR T.Analyzing and comparing montgomery multiplication algorithms[J].IEEE,Micro,1996,16(3):26-33.
[9] SATOH A,TAKANO K.A scalable dual-field elliptic curve cryptographic processor[J].IEEE.Transactions on Computers,2003,52(4):449-460.
[10] NEDJAH N,MOURELLE L M.Three hardware architectures for the binary modular exponentiation:Sequential,parallel,and systolic,IEEE Trans.Circuits Syst.I.Reg.2006,53(3):627–633.

