文献标识码: A
DOI:10.16157/j.issn.0258-7998.172462
中文引用格式: 许钧南,魏以民,苏巧,等. 基于四阶循环多谱的频谱感知算法[J].电子技术应用,2018,44(3):99-102,107.
英文引用格式: Xu Junnan,Wei Yimin,Su Qiao,et al. A spectrum sensing algorithm based on fourth-order cyclic polyspectrum[J]. Application of Electronic Technique,2018,44(3):99-102,107.
0 引言
随着无线通信技术的飞速发展,急剧增长的用户需求和有限的无线电频谱资源之间的矛盾越发凸显。1999年,MITOLA J博士提出认知无线电的概念[1],它能够智能感知频谱环境和伺机灵活接入频谱,实现频谱使用与需求的动态最优搭配,极大地提高了频谱利用率。在认知无线电系统中,认知用户为充分利用频谱空穴,同时避免对主用户产生干扰,必须对外界的频谱使用情况进行快速和准确的探测,因此频谱感知是认知无线电技术实现的前提。
传统的频谱感知方法有匹配滤波检测算法、能量检测算法和循环平稳检测算法[2]。匹配滤波检测算法是理论上最优的频谱感知方法,但需要主用户信号的先验信息不符合实际使用的要求[3]。能量检测是一种盲频谱感知算法,实现难度低,但易受噪声干扰,在低信噪比环境下性能不佳[4]。循环平稳检测算法在检测中无需任何先验信息,其利用信号的循环平稳特征实现频谱感知,可以有效抑制噪声,获得较好的检测性能[5]。
目前,大部分循环平稳检测算法均是基于信号循环谱密度(Cyclic Spectral Density,CSD)实现的[6-8]。文献[6]提出了一种低复杂度的盲频谱感知方法,利用CDS的幅度平方和作为判断主用户存在的统计量。文献[7]将神经网络与信号CSD检测相结合,提出了一种智能的频谱感知算法。以上频谱感知方法都有一个基本的假设:信道中的噪声是平稳噪声。然而在实际应用中,非平稳噪声是非常普遍的。由于信号的CDS本质上是二阶循环统计量,无法抑制非平稳噪声。因此,基于CDS的频谱感知方法仅能够适用于平稳噪声环境。
针对以上问题,本文提出一种非平稳噪声环境中基于四阶循环多谱的频谱感知算法。信号的四阶循环多谱(Fourth-Order Cyclic Polyspectrum,FOCP)理论上可以完全抑制任何平稳或非平稳的高斯有色噪声[9],而二阶循环统计量却没有这一优点。本文利用高阶累积量的切片形式[10]简化FOCP的计算,并将简化的FOCP与认知用户的极大似然检测相结合,得到简化的FOCP幅度平方和(the Sum value of the magnitude Square of the simplified FOCP,SS-FOCP)。最后,该算法通过计算SS-FOCP的峰值系数[11]判断主用户是否存在。仿真结果表明,本文的算法可以有效地适用于加性非平稳噪声环境,检测性能比传统的能量检测算法和CDS检测算法有明显提高。
1 系统模型
在加性噪声环境中,认知用户判断主用户是否存在的频谱感知问题,可以表示为如下假设检验模型[12]:

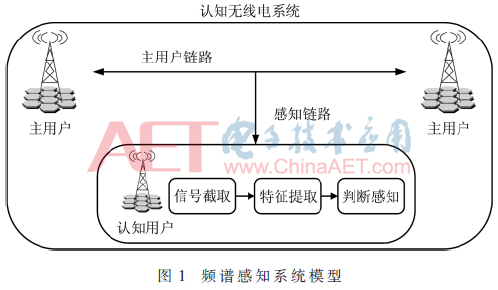
式中,x(t)和s(t)分别为认知用户截取的信号和主用户发送的信号。本文中,n(t)为加性非平稳高斯噪声。H0、H1分别表示为主用户信号s(t)不存在和存在两种情况。频谱感知的基本思路是:认知用户截取主链路中的信号,并通过循环平稳特征提取,最终判断主用户是否存在。频谱感知的系统模型如图1所示。
2 基于四阶循环多谱的频谱感知算法
2.1 四阶循环多谱的切片形式
假设认知用户截取的xT(t)是一段时长为T的连续实值循环平稳信号,则xT(t)在循环频率(Cycle Frequency,CF)α处的CSD可以表示为:

其中:
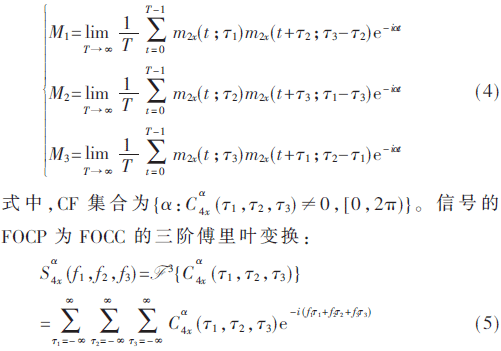
分析式(3)~式(5),可以发现信号的FOCC和FOCP结构复杂,计算量大。为了简化计算,本文引入累积量的切片形式计算FOCC和FOCP。
设式(3)~式(5)中τ1=τ2=0,能够得到FOCC和FOCP沿着τ3的切片形式。由于τ1、τ2、τ3是对称的,所以沿着任意一个轴对FOCC和FOCP取切片形式都是相同的。因此,FOCC沿τ3的切片形式可以表示为:

信号的S-FOCP继承了FOCP的性质,且S-FOCP的计算复杂度要明显小于FOCP。对比式(9)和式(2),发现信号的S-FOCP与CSD在数学形式上相似,有利于下一步的分析。
2.2 简化的FOCP幅度平方和(SS-FOCP)
根据式(1)给出的假设检验模型,基于CDS的认知用户极大似然检测器可以表示为[9]:

由于信号的S-FOCP能够有效抑制任何平稳和非平稳噪声,所以在 因此,式(11)可以进一步简化为:
因此,式(11)可以进一步简化为:
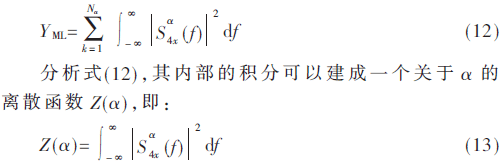
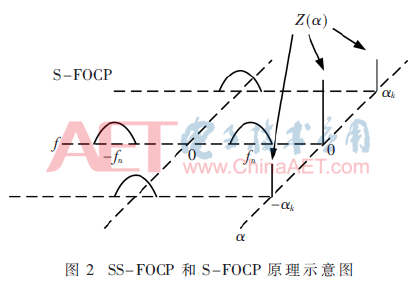
式中,Z(α)即为SS-FOCP,其反映了信号在各CF点上S-FOCP的大小。因为信号的S-FOCP仅在CF点上不为零,所以Z(α)在不同CF点上拥有不同脉冲值。通过检测信号SS-FOCP的变化,能够有效判断主链路中的情况,实现频谱感知。信号SS-FOCP与S-FOCP的原理如图2所示。
2.3 SS-FOCP的峰值系数
由于SS-FOCP是脉冲序列,本文选用SS-FOCP的峰值系数作为特征参数,检测主用户信号的存在。峰值系数能够反映序列波动程度的大小,常被运用到信号的检测与提取当中,其数学表达式为[11]:
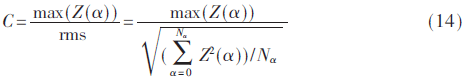
式中,rms表示均方根。假设主用户没有使用主链路,认知用户截取的信号仅包含噪声,检测器此时能够获得噪声的SS-FOCP,并计算其的峰值系数,设置判断门限Cth。因此,基于FOCP的二元假设检验模型为:

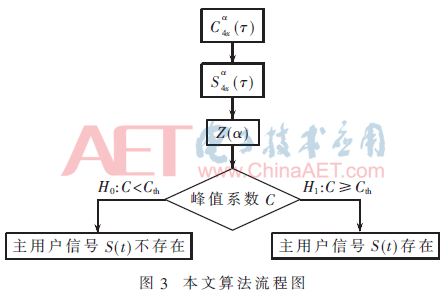
综上所述,基于FOCP的频谱感知算法的流程如图3所示。
3 仿真与性能分析
在仿真中,假设主用户信号采用QPSK调制方式,信号被截取长度为120 bit,蒙特卡洛实验次数为1 000次。为反映非平稳噪声的不稳定性,本文假设噪声方差的不确定度为ρ dB,其方差值在 范围内随机波动。
范围内随机波动。
图4给出了BPSK、QPSK、8PSK和MSK 4种调制信号在无噪声环境中的SS-FOCP。由图4可知,在无噪声环境中,每种调制方式均具有不同的SS-FOCP,且在不同CF点上脉冲值差距明显。因此,通过观测截取信号的SS-FOCP,能够较好地识别采用不同调制方式的主用户信号,实现频谱感知。
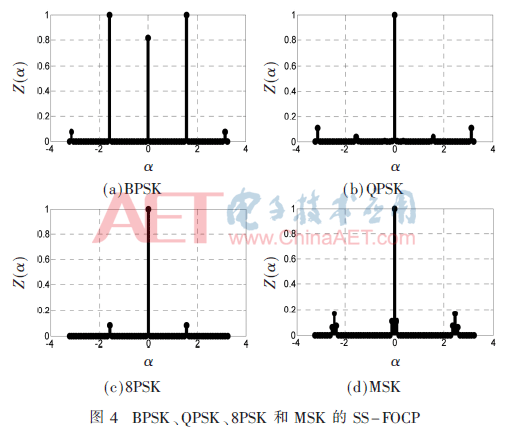
图5给出了当信噪比为-10~10 dB时,H1假设下截取信号峰值系数Cx与H0假设下非平稳噪声峰值系数Cn的曲线变化示意图。仿真中,假设非平稳噪声的不确定度ρ=3 dB。实验发现当SNR≥-1 dB时,Cx明显大于Cn,且两者均保持稳定。当SNR∈[-7 dB,-1 dB)时,信号SS-FOCP受到非平稳噪声的影响出现变化,Cx随着SNR的减小开始衰落。当SNR<-7 dB时,Cx与Cn大小相近,仅略大于Cn,二者最终均保持稳定。因此,通过计算峰值系数,能够检测到主链路中信号的变化情况,证明了其作为频谱感知特征参数的有效性。

在ρ=3 dB的非平稳噪声环境下,对能量检测算法、基于CDS的检测算法和本文算法进行性能检测,其识别概率Pd与信噪比关系的曲线如图6所示。其中,ED表示能量检测算法,CD表示基于CDS的检测算法,FOCP表示本文算法。

由图6可见,在非平稳噪声环境下,本文算法的识别概率曲线Pd要明显优于能量检测算法和基于CDS的检测算法。当SNR=-10 dB时,本文算法的Pd要比能量检测和基于CDS的检测算法分别高62.3%和51.6%。非平稳噪声严重影响了能量检测算法的性能,对基于CDS的检测算法也造成了一定的干扰。本文算法利用FOCP的性质,较好地抑制了非平稳噪声的影响,其检测性能最好,受到的影响最小。
图7给出了当非平稳噪声的不确定度不同时,本文算法的识别概率Pd与信噪比关系的曲线。由图7可知,当SNR=-10 dB时,ρ=7 dB噪声环境下的Pd分别要比ρ=3 dB和ρ=5 dB的情况下低37.7%和26.5%。同一信噪比条件下,随着非平稳噪声的不确定度增大,本文算法的识别概率变低,检测性能逐渐下降。

4 结论
本文将FOCP运用到频谱感知当中,利用信号FOCP抑制信道中的非平稳噪声性质,并简化FOCP的计算,提出了基于FOCP的频谱感知方法。通过仿真结果可以看出,本文算法对比传统的能量检测算法和基于CDS的检测算法,能够更好地适用于非平稳噪声环境,其识别概率更高,性能更好。同时,信号的SS-FOCP及其峰值系数能够较好地反映主链路中的实际使用情况,识别采用不同调制方式的主用户信号,实现频谱感知。
参考文献
[1] MITOLA J,MAGUIRE G Q.Cognitive Radio:Making soft-ware radios more personal[J].IEEE Personal Communication,1999,6(4):13-18.
[2] Liu Chang,Li Ming,Jin Minglu.Blind energy-based detection for spatial spectrum sensing[J].IEEE Wireless Communications Letters,2015,4(1):98-101.
[3] URRIZA P,REBEIZ E,CABRIC D.Multiple antenna cyclostationary spectrum sensing based on the cyclic correlation significance test[J].IEEE Journal on Selected Areas in Communications,2013,31(11):2185-2195.
[4] ZHANG W,MALLIK R K,LETAIEF K B.Optimization of cooperative spectrum sensing with energy detection in cognitive radio networks[J].IEEE Transactions on Wireless Communications,2009,8(12):5761-5766.
[5] PO K,TAKADA J,KIM M.Performance evaluation of cyclic detector in cognitive radio[R].Japan:Hiroshima International University,2007.
[6] JANG W M.Blind cyclostationary spectrum sensing in cognitive radios[J].IEEE Communication Letters,2014,18(3):393-396.
[7] 赵知劲,陈京来.蜂群优化神经网络的频谱感知[J].信号处理,2016,32(1):77-82.
[8] 刘帅,谭学治,张南.循环平稳特性检测频域设计及信噪比估计研究[J].电子技术应用,2010,36(2):114-117.
[9] DANDAWATE A V,GIANNAKIS G B.Nonparametric polyspectral estimators for kth-order cyclostationary processes[J].IEEE Transaction on Information Theory,1994,40(1):67-84.
[10] SHEN Z H,TANG B,LV Y,et al.Multiple parameters estimation simultaneously for DS-SS/BPSK signal based on Fourth-Order cumulant 2-D Slice[J].Proceeding of ICCCAS,2004,2(1):867-870.
[11] GARDNER W A,SPOONER C M.Signal interception: performance advantages of cyclic-feature detectors[J].IEEE Transactions on Communications,1992,40(1):149-159.
[12] 李微,宋晓勤,牛英滔,等.认知无线电中能效优先的频谱感知算法研究[J].测控技术,2017,36(4):14-17.
[13] 张贤达.时间序列分析——高阶统计量方法[M].北京:清华大学出版社,1996.
作者信息:
许钧南,魏以民,苏 巧,邓昌良,沈越泓
(陆军工程大学 通信工程学院,江苏 南京210000)

