0 引言

    电力场效应管具有驱动电路简单、驱动功率小、热稳定性好、开关速度快、工作频率高的特点，常作为高频开关电源的核心器件，被广泛应用于电力电子的通信电源设备^[1]。然而，P-MOSFET在大功率、强电流的开关工作状态下，其内部的导通电阻迅速增大，导致P-MOSFET产生电导调制效应，极大地限制了其开关速度，影响其击穿电压，直接影响P-MOSFET的可靠性^[2-3]。已有相关文献显示，当P-MOSFET可靠性降低时，其内部的RTS噪声成分显著，可以作为反映P-MOSFET可靠性的敏感参数^[4]。因此对P-MOSFET的RTS噪声检测与分析是研究P-MOSFET可靠性的当务之急。

1 P-MOSFET管RTS噪声的检测

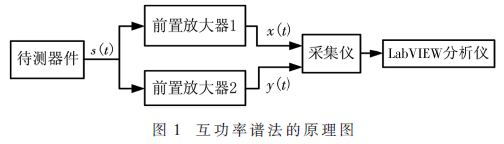
    传统的低频噪声测量是将放大器直接与频谱分析仪相连^[4]，很难辨别RTS噪声的来源，而且RTS噪声极其微弱，很容易被放大器的背景噪声所掩埋。因此本文根据互谱法的原理，可采用二通道互谱测量方法对电力场效应管的RTS噪声进行检测。

1.1 互谱测量

    互谱测量的原理如图1所示，其中 s(t)为待测P-MOSFET经过偏置电路所激发的低频噪声，x(t)和y(t)分别为放大器1和2的输出信号。

    由互谱测量的原理可得出^[5]：

式中，T为测量的时间，t为时间变量，τ为x(t)与y(t)迟延，j为虚单位，ω为系统的角频率。

    根据上式可知，如果测量的时间比较长，两个通道之间的背景噪声便可以充分抑制，就削弱了系统的干扰噪声对待测RTS噪声的影响。

1.2 改进型EMD算法的实现

    根据EMD算法的流程图^[6]，可知EMD算法能够对其所含有各种频段的噪声进行逐层分解，但无法有效地滤波以及恢复出含有其他噪声成分较小RTS噪声。因此，提出了一种改进型的EMD算法。

    改进的思路如下：

    (1)利用EMD对RTS噪声进行分解得到：

式中f(t)为待测样品的RTS噪声信号，n为EMD分解的层，j为 EMD分解的第j层，t为时间，IMF_j为经EMD分解后的第j层的本征模态分量，r_n(t)为分解n层之后余下的残波。

    (2)根据IMF分量的频率具有依次递减的特点，找出高低频干扰成分显著的IMF分量集合C和D。

    高频分量集合：

    C={IMF₁，IMF₂，…，IMF_k}且k<n

    低频分量集合：

    D={IMF_n，IMF_n-1，…，IMF_l}且l<n-k-1

    (3)让原始的RTS噪声信号减去高频干扰主要集中的成分C与低频扰动集中的D成分，即可滤除噪声，得到背景噪声较小的RTS噪声信号，其表达式为：

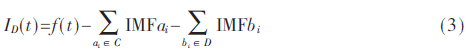
式中I_D(t)为滤波后的RTS噪声信号，a_i为高频分量集合C中的IMF任意高频分量，b_i为低频分量集合D中的IMF任意低频分量。

    图2(a)为文献[6]采用的高通数字滤波器的方法处理样品RTS噪声后的滤波效果，通过比较图2(a)与图2(b)可以看出经过EMD处理后的噪声信号，能够很好地滤除RTS噪声信号中的高频干扰，滤波效果优于传统的方法，分离出比较理想的三电平值RTS噪声。

1.3 改进的自适应最小均方算法

    虽然改进型的EMD算法能够有效地消除高低频干扰对RTS噪声的影响，但不易确定EMD分解后的高低频干扰IMF分量，尤其是当待分解的RTS噪声含有较大的干扰时，EMD分解的层数就会较多，对含有高低频成分的IMF分量C与D的确定就更加困难。

    因此，可以利用改进型的自适应最小均方（Least-Mean-Square，LMS）算法克服以上问题。其改进的自适应LMS算法的思路为：

    (1)初始化参量阵元个数M、参考信号d(n)。

    (2)由W(n+1)=W(n)+2μ(n)e(n)X(n)计算初始状态下的权W，并得出所得信号与期望信号之间的误差。

    (3)为了加快改进型EMD算法收敛的稳定性，减少EMD分解的层数，根据改进型的公式μ(n)=1/(rho_max+1)(其中rho_max为RTS噪声相关矩阵的最大特征值)计算步长因子μ(n)。

    (4)根据迭代公式算法计算W(n+1)。

    (5)由新得到的权值W(n+1)计算新的输出信号及其与目标信号之间的误差。

    (6)根据第5步得出的误差大小判断是否达到误差允许范围的要求。若误差满足要求，则迭代结束，所得的权值向量W(n+1)即是要求的目标权值；否则转向第3步迭代继续进行。

    经自适应LMS算法滤波后的RTS噪声如3所示，由图3(b)可知，滤波后的效果优更为接近理想的三电平值的RTS噪声。

2 P-MOSFET管 RTS噪声的分析

    由于传统的分析方法不再适用于RTS噪声的时域分析，而高阶累积量可以用于对非高斯信号的分析，因此本文提出了利用高阶累积量来分析RTS噪声。

2.1 高阶累计量的优化

    由于RTS噪声的时间分布函数呈现泊松分布，因此为了分析优化得到的高阶累积量的性能和有效性，可以运行时间和波形相关系数(Normalization Cross Correlation，NCC)来分析四阶累积量进而分析RTS噪声信号：

式中：x(n)为原始信号，x′(n)为x(n)转置函数，L、m分别为x(n)、x′(n)的采样数。运行时间越小，波形相关系数越大，则算法性能更好。

2.2 高阶累积量的优化验证

    为验证该优化算法的有效性，在LabVIEW平台下将RTS噪声信号导入数据库，利用NCC分别对RTS噪声的四阶累积量进行优化处理，得到的结果如图4所示。

    从图4可以看出，RTS噪声的四阶累积量都呈现泊松规律，进一步验证了RTS噪声的时间分布函数服从泊松分布的规律。在零频处有一个很明显的尖峰，具有1/f噪声特性，而且四阶累积量峰值明显多于四阶累积量，也说明了RTS噪声是1/f噪声叠加的过程。同时图形当中每个点都在零平面附近对称的跳动，从而证明RTS噪声四阶累积量为零，进而验证本算法的正确性、可行性。

    同时对优化前后的四阶累积量仿真结果显示优化前的时间为16.26 s，优化后的仅为为9.248 s，说明优化后四阶累积量减小了运算时的复杂度，提高了对RTS噪声数据处理的效率。

3 结论

    本文通过互谱测量法测量出P-MOSFET管的RTS噪声，利用了改进型的EMD算法与LMS算法对其逐层分解、滤波、恢复出较为理想的RTS噪声信号，并对高阶统计量的算法进行了优化，验证了RTS噪声的时间函数呈现的泊松分布规律，证明该方法的正确与有效性。

参考文献

[1] MOHAMED N，DEBARSHI B，CELIK B.Variability of random telegraph noise in analog MOS transistors[J].Noise and Fluctuations，2013，15(8)：275-290.

[2] 陈晓娟，樊欣欣，吴洁．短沟道MOS器件随机电报信号噪声的检测与分析[J].半导体技术，2016，41(3)：234-239.

[3] LEYRIS C，MARTINEZ F，VALENZA M，et al.Random telegraph signal：a sensitive and non destructive tool for gate oxide single trap characterization[J].Micro Electronics Reliability，2014，47(6)：573-576.

[4] LEE A，BROWN A，ASENOV A，et al. Random telegraph signal noise of power MOSFETs subject to atomic scale structure variation[J].Superlatives and Microstructures，2014，39(12)：293-300.

[5] 孙玮，孙钊，王鹏.场效应晶体管随机电报信号噪声的探测及分析[J].西安工业大学学报，2013，16（12）：957-960，967.

[6] 陈晓娟，樊欣欣.基于RTS噪声测量与参量的提取[J].电力电子技术，2016，50(8)：103-105.

[7] 樊欣欣，杨连营，陈秀国.基于低频噪声检测的电力MOSFET可靠性分析[J].半导体技术，2018(1)：75-80.

作者信息:

樊欣欣，杨连营，陈秀国，徐  斌

（国网铜陵供电公司，安徽 铜陵244000)