文献标识码: A
DOI:10.16157/j.issn.0258-7998.190704
中文引用格式: 陈吉成,陈鸿昶,李邵梅. 利用非重叠CD生成解的集成重叠社区检测[J].电子技术应用,2019,45(12):96-100,105.
英文引用格式: Chen Jicheng,Chen Hongchang,Li Shaomei. Integrated overlapping CD method using existing solutions of non-over-lapping CD[J]. Application of Electronic Technique,2019,45(12):96-100,105.
0 引言
现实世界网络具有复杂性、高维性和多面性,其基本属性是网络的“社区结构”,通常假定为社交网络中的组织单元[1]、引文网络中的科研社区[2]等。虽然社区检测(CD)的研究较早,但其依然是个具有挑战性的复杂问题,主要体现在:(1)CD问题没有明确的定义,针对同一个网络可以得到多个解,且每个解都有其自身的重要意义;(2)现实世界网络的顶点常属于多个社区[3-4],导致重叠的社区结构。
传统的CD算法大多假定社区是非重叠的,如基于顶点相似性的算法[5]、基于显著性的算法[6]、基于模块优化的算法[7]等。在现实世界中,一个顶点属于多个社区,从而产生重叠社区结构。因此也有一些重叠CD算法,如文献[8]提出了基于扩展激活的标签传播算法(LPAEA),用于动态社交网络中的重叠社区检测;文献[9]加强了节点自身的内容特性,提出了增广网络的CD算法。
此外,在数据挖掘中,也经常利用集成方法进行数据点聚类。如文献[10]将CD问题建模为一个单目标优化问题,提出了一个新的Memetic算法,通过优化模糊度评价指标检测复杂网络中的重叠社区结构,并使用“一致续存”度量来修改给定的非重叠社区结构;文献[11]提出的集成算法MEDOC使用了元社区的概念,利用基础非重叠社区结构来创建多分体网络,通过隶属函数来确定顶点对社区的隶属性。
由于非重叠CD算法会从一个网络中生成大量(且显著不同的)社区结构,本文利用该信息来提取与每个顶点相关联的隐性特征信息,提出了一种集成重叠社区检测方法(IOCD),充分利用了非重叠CD的生成解。实验结果表明,所提IOCD的性能优秀,框架具有良好的通用性。因此,在网络拓扑不完整、本质上具有稀疏性且顶点属性可用的情况下,可利用所提框架将特征合并到模型中以进行重叠社区检测。
1 提出的算法概况

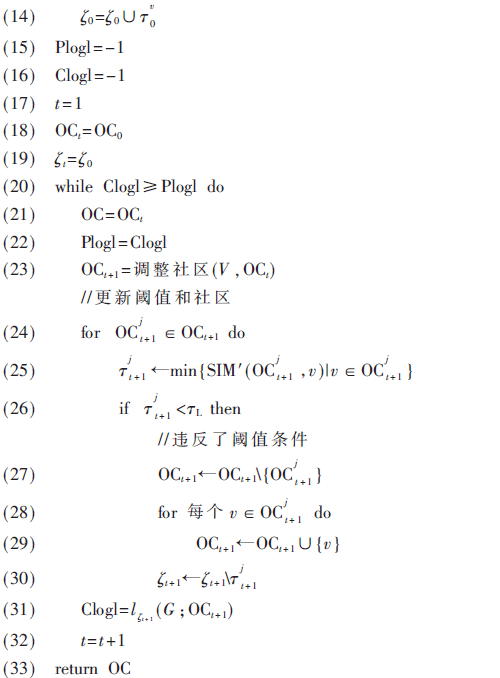

本文设计IOCD算法,以最大化社区内每个节点的隶属可能性。IOCD首先在网络上以不同的顶点顺序运行所有的基础非重叠CD算法,得到不同的基础社区结构。除此之外,利用基础社区信息为每个顶点生成特征向量,由此将网络中的顶点转换为特征空间。每次迭代中,算法通过从指定社区中随机移除顶点并将其分配至一些未指定社区,以调整社区结构[12],由此避免违反相似性条件。在每次迭代后,对每个社区相关的相似性阈值进行更新。持续进行迭代,直至目标函数的数值开始下降。
2 算法实现细节
2.1 生成顶点的特征向量

2.2 目标函数
首先,定义目标函数需要明确几个度量。

其中,每个社区均关联到一个最小相似度阈值,每个顶点必须满足该阈值才能成为相应社区的一部分。
(3)每个社区的相似度阈值:在提出的模型中,每个社区OCj均被分配一个相似度阈值τj,若顶点v∈V在OCj中,则其应该满足SIM′(OCj,v)≥τj。给定OC={OC1,OC2,…},一个重叠社区结构和阈值集合ζ={τ1,τ2,…},根据两个顶点在不同的重叠社区中的隶属性,定义这两个顶点之间的隶属相似度。
(4)逐对顶点的隶属相似度:根据顶点u和v在不同社区中的隶属性来定义两个顶点之间的隶属相似度:


算法将式(8)中的目标函数最大化(算法1第31行),以得到最终重叠社区结构OC。
2.3 更新阈值并计算目标函数


2.4 复杂度分析
当目标函数达到最大值且不发生进一步变化时,IOCD终止。最差情况下,在任意一次迭代后,重叠社区的最大数量为|V|,每个社区内顶点最大数量也为|V|。由此,每次迭代后的运行时间为O(|V|+|OC|)。需注意的是,只有在对数似然值增加的情况下,才可以对当前社区结构进行调整。因此,IOCD通常会在有限次数的迭代后收敛。实践中,本文假定如果对数似然值在|V|次迭代后不发生变化,则达到局部最大值。此外,IOCD是一个集成算法,需要运行所有基础算法,其优化途径之一是基础算法的并行化。
3 实验结果与分析
3.1 数据集
本文使用了两类网络数据集:
(1)合成网络:利用LFR基准模型[10]来生成合成网络及社区。参数配置如下:顶点数量N=10 000;平均度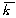 =50;最大度kmax=150;最大社区规模cmax=150;最小社区规模cmin=50;重叠顶点百分比On=15%;一个顶点所属的社区数量Om=20;混合参数μ=0.3(表示社区间和社区内的边的比率;?滋数值越低,表示社区质量越高)。针对每个配置创建100个LFR网络,并报告平均结果。
=50;最大度kmax=150;最大社区规模cmax=150;最小社区规模cmin=50;重叠顶点百分比On=15%;一个顶点所属的社区数量Om=20;混合参数μ=0.3(表示社区间和社区内的边的比率;?滋数值越低,表示社区质量越高)。针对每个配置创建100个LFR网络,并报告平均结果。
(2)现实世界的社区网络:使用2个不同规模的现实网络,且为先验可用,如表2所示。

3.2 度量
为比较检测到的重叠社区结构,本文使用了3个标准度量:(1)重叠归一化互信息(ONMI)[14];(2)Ω指标[7];(3)F测度[7]。
3.3 评价分析
本文在LFR网络和2个真实世界网络上运行IOCD与其他3个重叠CD算法,这3个算法分别是:文献[8]提出的基于扩展激活的标签传播算法(LPAEA);文献[10]提出的Memetic算法,将CD问题建模为一个单目标优化问题;文献[11]提出的集成算法MEDOC,使用了元社区的概念。实验通过3个评价指标对输出进行比较。表3~表5分别给出了在ONMI、Ω指标和F值方面的性能。整体上,IOCD表现出最优性能,其次为MEDOC[11]。IOCD在所有网络上的绝对平均值ONMI为0.82。IOCD的Ω指标和F值的绝对平均值分别为0.82和0.83。
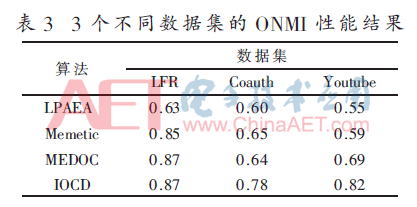
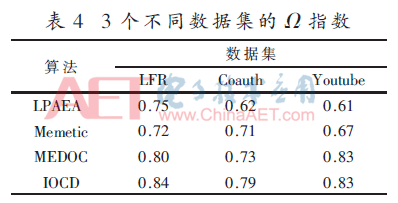
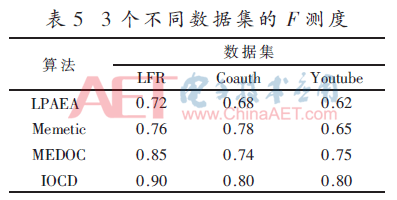
所提IOCD的性能明显优于LPAEA[8]、Memetic[10]和MEDOC[11]的可能原因列举如下。Memetic和MEDOC的最终性能取决于单个CD算法的性能。Memetic在找到单个非重叠社区结构后,通过后处理步骤发现重叠属性,因此重叠社区结构的质量取决于最初找到的非重叠社区结构。LPAEA利用未标签的数据来捕捉整个数据的潜在分布,相似的数据必须要有相同的标签,对CD算法有一定依赖性。MEDOC利用CD算法,对利用基础非重叠社区结构所创建的多分体网络进行划分,因此最终重叠社区结构的质量取决于在多分体网络上使用的CD算法的性能。另一方面,IOCD通过多个非重叠CD算法给出的非重叠社区结构来取得顶点特征,并以优化后的设置来使用这些特征。因此,IOCD的性能不取决于任何一个CD算法,能够从多个非重叠社区结构中进行有效学习。
3.4 参数选择分析
本文通过将混合参数μ从0.1~0.8之间变化(以0.1递增),在LFR网络上进行实验,涉及的主要参数问题如下。
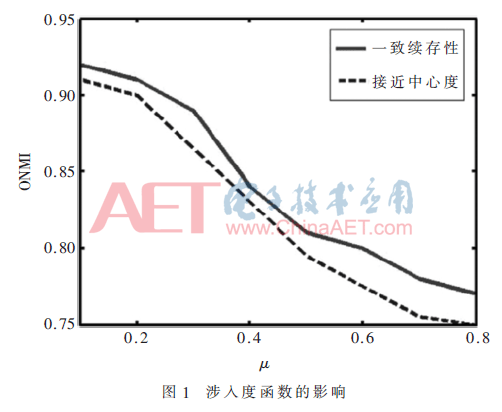
(1)涉入度函数(INV):以下两个函数用于量化顶点在社区中的涉入程度:

涉入度函数如图1所示,混合参数μ从0.1~0.8之间变化(以0.1递增)。可以看出,所提IOCD在使用一致存续性度量时始终取得了较好性能。
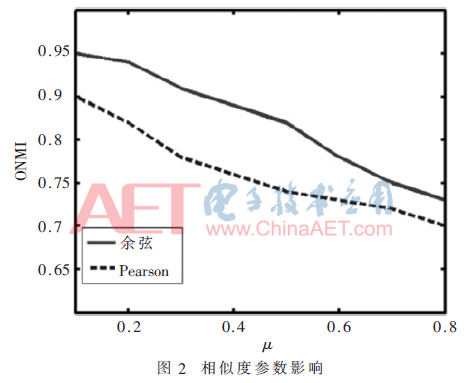
(2)两个顶点之间的相似度(SIM):本文在2.2节提到了利用余弦相似性来测量两个顶点的特征向量之间的相似度,但本文还使用了Pearson相关系数测量了两个特征向量之间的相似度。结果表明,余弦相似性度量的性能优于Pearson相关系数,如图2所示。
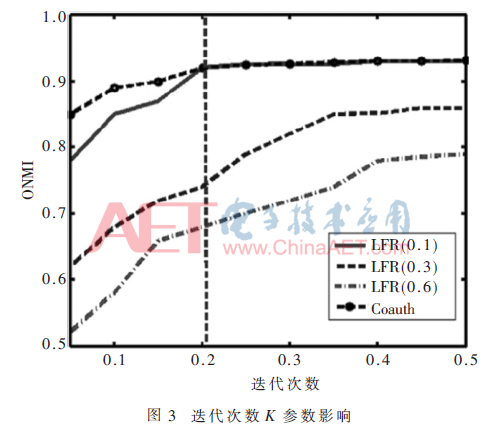
(3)迭代次数(K):根据网络中顶点的数量N来设定K。图3的分析表明,对于大部分网络,特别是具有独特社区结构的网络(例如混合参数μ=0.1的LFR网络),IOCD的性能会在K=0.2|V|处收敛,因此,将K=0.2|V|作为默认值。
4 结论
本文充分利用了非重叠CD的生成解,将解的信息与每个顶点相关联的隐性特征信息,利用多个非重叠CD算法的输出进行重叠社区检测,所提IOCD几乎不受基础CD算法的影响。多个数据集上的实验结果表明,所提IOCD优于一些同类CD算法。未来可能通过相关性研究或基于机器学习的方法来提升CD算法的求解效率。
参考文献
[1] 刘天华,殷守林,李航.一种新的在线社交网络的隐私保护方案[J].电子技术应用,2015,41(4):122-124.
[2] 罗双玲,张文琪,夏昊翔.基于半积累引文网络社区发现的学科领域主题演化分析——以“合作演化”领域为例[J].情报学报,2017,36(1):100-110.
[3] YANG J,LESKOVEC J.Overlapping community detection at scale:A nonnegative matrix factorization approach[C].Proceedings of the Sixth ACM International Conference on Web Search and Data Mining.ACM,2013:587-596.
[4] 崔俊明,李勇,李跃新.基于非加权图的大型社会网络检测算法研究[J].电子技术应用,2018,44(2):86-89,93.
[5] 陈晓,郭景峰,张春英.社会网络顶点间相似性度量及其应用[J].计算机科学与探索,2017,11(10):1629-1641.
[6] ANDREA L,FILIPPO R,RAMASCO JOSE J,et al.Finding statistically significant communities in networks[J].PLOS ONE,2011,6(4):61-71.
[7] 阙建华.社交网络中基于近似因子的自适应社区检测算法[J].计算机工程,2016,42(5):134-138.
[8] HUANG M,ZOU G,ZHANG B,et al.Overlapping community detection in heterogeneous social networks via the user model[J].Information Sciences,2018,38(4):164-184.
[9] 蒋盛益,杨博泓,姚娟娜,等.一种基于增广网络的快速微博社区检测算法[J].中文信息学报,2016,30(5):65-72.
[10] 郭杨志.复杂网络社区结构的重叠社区发现和鲁棒性分析[D].西安:西安电子科技大学,2018.
[11] CHAKRABORTY T,PARK N,SUBRAHMANIAN V S.Ensemble-based algorithms to detect disjoint and overlapping communities in networks[J].ASONAM,2016,45(12):73-80.
[12] 龙浩,汪浩.复杂社会网络的两阶段社区发现算法[J].小型微型计算机系统,2016,37(4):694-698.
[13] KANAWATI R.YASCA:an ensemble-based approach for community detection in complex networks[M].Computing and Combinatorics. Springer International Publishing,2014.
[14] HAJIABADI M,ZARE H,BOBARSHAD H.IEDC:an integrated approach for overlapping and non-overlapping community detection[J].Knowledge-Based Systems,2017,43(3):188-199.
[15] 陈晓,郭景峰,张春英.社会网络顶点间相似性度量及其应用[J].计算机科学与探索,2017,11(10):1629-1641.
作者信息:
陈吉成,陈鸿昶,李邵梅
(国家数字交换系统工程技术研究中心,河南 郑州450002)

