计算机断层成像技术CT(Computed Tomography)作为一种新型的成像方式已经被广泛应用于医学、工业等领域。三维CT相对于传统二维CT有空间分辨率高，各向同性的优势[1]。但是由于三维图像重建运算量大，重建时间长的问题已成为制约其走向实用的瓶颈。
    目前，重建加速研究主要集中在通过改进算法的软件加速及利用GPU、FPGA进行的硬件加速。其中，FPGA由于具有极佳的并行计算能力及可重构可定制的特点[2]，利用FPGA实现CT重建加速正逐渐引起研究人员的注意。
    2002年Miriam Leeser[3]首次利用FPGA对二维CT重建进行了加速，重建规模为512^2时需要3.6 s。2003年Iain Goddard[4]首次对三维CT重建FDK算法中的反投影过程用FPGA实现加速，重建规模为512^3时，反投影过程需要38.7 s；2008年Benno Heigl[5]用9块FPGA协调配合完成了FDK算法中滤波及反投影部分的加速，重建规模为512^3时，该过程共需要9 s。2009年Nikhil Subramanian[6]利用FPGA作为协处理器用Impulse c语言开发实现了二维CT重建过程的加速，重建规模为512^2时，反投影过程需要38.4 ms。
　    在FPGA内实现硬件加速是通过全数据流的形式处理，脱离了指令的操作。为了充分利用FPGA的片内资源以获得更高的加速效果，本文设计了一种并行无等待流水线的处理结构，同时对核心算法电路进行资源优化，在保持高度并行性的同时保证了较高的资源利用率。
1 FDK算法
    
     

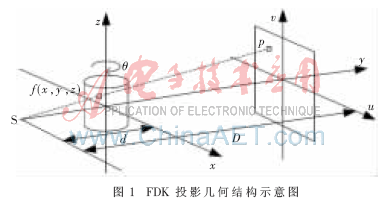
    在FDK算法中，反投影的计算复杂度与时间消耗都是最大的，是制约重建速度的瓶颈所在，因此本文研究在FPGA内实现反投影部分的加速方法。
2 FPGA反投影加速实现
    反投影过程需要对重建物体旋转一周所采集到的数据进行处理。实际情况中采集数据的过程是离散的，且每一个分度下投影数据的处理过程不相关。基于这种可并行性，用FPGA加速的思路是并行计算反投影过程，并且在保证每一个反投影单元速度最快时并行尽可能多的反投影单元。
2.1 无等待流水线的设计
    重建物体体素的反投影流程有3个步骤。首先根据图1的几何关系定位出重建体素在探测器上的位置；然后从存储器中读取相应数据；最后对所读取数据进行双线性插值。
    通过流水线设计，双线性插值部分可以在每一个时钟更新一个数据，但是每更新一个数据需要从数据存储空间读取4个数据来计算，如果花费4个时钟周期来读取这4个数据，就会造成前级数据读取时间大于后级双线性插值时间，双线性插值处理单元会产生空泡。空泡的产生，不但制约了后级处理单元的计算速度，也造成FPGA内资源利用率的降低。
    为了解决上述问题，提高处理速度以及资源利用率，分析双线性插值过程所读取4个数据之间的关系，如图2所示。

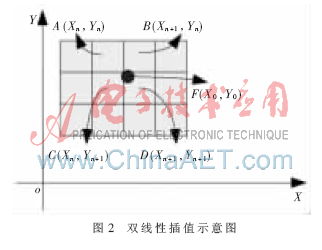
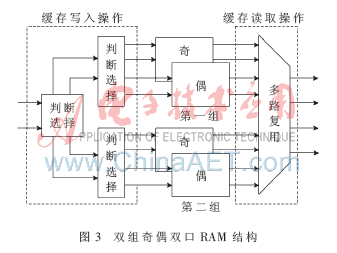
    图3中两组共四个存储空间均为FPGA片内设计的双口RAM。通过数据预取技术以及两组RAM之间的乒乓操作避免了双线性插值时随机访问外部存储器带来的延迟。在反投影处理中，第一组RAM处于数据写入过程时，分别向该组两块RAM写入探测器上奇数行数据与偶数行数据。同时另一组RAM中的数据进行双线性插值。计算完成后，两组RAM进行读写状态的互换，完成一次乒乓循环。在投影寻址单元中，计算出A(Xn，Yn)的纵坐标Yn，对其奇偶性进行判断，当其为奇数时，从两块RAM中所取数据与地址分别为：
   

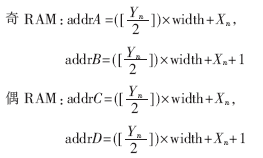
    通过这种双组奇偶双口RAM缓存结构的设计在不增加片内存储资源消耗的前提下一个时钟周期内取出四个数据，消除了空泡，实现了无等待流水线，在一个时钟周期内可更新一个重建点的结果。
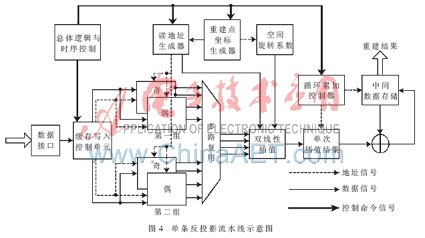
    单条反投影流水线设计原理如图4所示。图中总体逻辑与时序控制模块通过状态机实现对流水线的控制；缓存写入控制单元对投影数据的写入操作进行判断与控制；重建点生成器产生重建点坐标，并根据此坐标由读地址生成器计算双线性插值数据的地址，同时通过查表找出空间系数sin?兹与cos?兹；循环累加控制器完成对各分度下反投影结果的归约过程。

2.2 并行流水线处理结构
    基于各个分度下反投影过程的不相关性，在FPGA内设计一种基于分度的并行流水线处理结构，如图5所示。数据控制接口以及时序状态控制模块完成对输入数据的分配调度，通过多条反投影流水线并行计算后，由循环归约单元完成反投影结果的归约。

    假如投影分度数为360，理想情况是在FPGA内部实现360条并行的反投影流水线，但由于FPGA片内资源的限制无法达到如此高的并行性，因此需要对每一次并行计算结果进行存储，并完成累加计算。设计循环归约单元完成上述操作。当有N条并行流水线并行计算
    
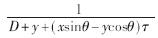
    在FPGA内设计时，预先算出该公因式的值，然后通过移位寄存的方法进行延迟同步，使之在相应的节拍打入到指定的计算单元。虽然这样增加了乘法运算，但是将三次除法运算优化为一次，节省了大量的资源。表1给出了优化前后资源占有情况对比。

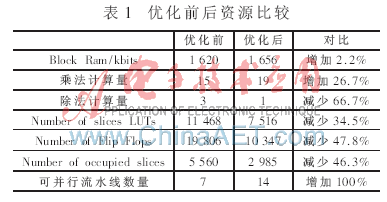
    通过优化，在XC5VLX330 FPGA内部可以并行14条反投影流水线，相比优化以前，流水线数增加1倍。
3 实验结果与分析
    通过编写Verilog语言程序，在XC5VLX330 FPGA上进行综合仿真，采取14条并行反投影流水线对Shepp-Logan标准体模进行重建，得到图6所示结果。

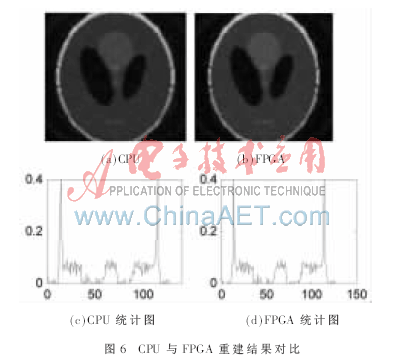
    图6(a)为CPU重建图像的一个切片，图6(b)为FPGA加速重建的图像切片，图6(c)，图6(d)分别为图6(a)，图6(b)切片图像中心横线的统计图，从图中可以看出FPGA加速重建结果的精度达到要求。表2给出FPGA与CPU对不同规模数据进行重建时速度对比，计算机CPU为Inter Xeon E5430 2.66 GB，内存为16 GB。

    可以看出，通过FPGA加速FDK算法中的反投影过程加速比达到了115，具有显著效果。获得加速比的原因由FPGA的体系结构所决定，其基于数据流的处理方式脱离了指令的操作，保证每一个时钟周期都是用来计算。当采取多条流水线并行处理时，加速比进一步提高，加速比与在FPGA内并行流水线数目成正比。
    本文在FPGA上实现了对三维CT重建过程的加速。针对FDK算法中计算复杂度最高的反投影过程，通过双组奇偶双口RAM的缓存结构实现了无等待流水线，达到每一个时钟周期可更新一个重建点的速度。另外通过优化电路设计降低了单条流水线的资源占有率，在XC5VLX330上实现了14条流水线的并行处理，在保证重建图像质量的同时，取得了115倍的加速比。在利用FPGA实现CT重建加速时，影响加速效果的主要因素是FPGA内部资源利用率以及数据传输效率，随着未来FPGA以及存储器技术的发展，FPGA可以实现更快的CT重建速度。
参考文献
[1] 包尚联.现代医学影像物理学[M].北京：北京大学医学出版社，2003.
[2] 刘佳，焦斌亮.FPGA的发展趋势及其新应用[J].电子技术，2008(4).
[3] LEESER M.Parallel-beam backprojection：an FPGA implementation optimized for medical imaging[J].Proc of the Tenth Int.Symposium on FPGA.2002(2)：217-226.
[4] GODDARD I.High-speed cone-beam reconstruction：an embedded systems approach[J].Proceedings of SPIE，2003：483-491.
[5] Benno Heig.High-speed reconstruction for C-arm computed tomography[C].Proceedings of the 9th International Meeting on Fully Three-Dimensional Image Reconstruction in Radiology and Nuclear Medicine.2008：25-28.
[6] Nikhil Subramanian.A C-to-FPGA solution for accelerating  tomographic reconstruction[D].University of Washington，
     2009.
[7] 张剑，陈志强.三维锥形束CT成像FDK重建算法发展综述[J].中国体视学与图像分析，2005(2)：116-121.