文献标识码: A
文章编号: 0258-7998(2015)02-0055-04
0 引言
Sigma-Delta(ΣΔ)加速度传感器利用了ΣΔ调制技术实现了数字输出,相对于传统加速度传感器系统,其对周围环境温度变化不太敏感,而且稳定性较好,尤其是其能够很方便地给后级数字处理单元提供直接数字输出,有利于系统的集成[1-2]。国外对于ΣΔ加速度传感器系统的研究开展得较早,取得的研究成果也较多。国内在相关的研究方面落后了很多,且主要集中于低噪声性能的研究[3-5]。然而谐波失真是加速度传感器误差的一个重要来源,目前针对其开展的研究并不多。文献[6]开展了一种闭环微机械加速度计的非线性研究,主要集中于结构生产工艺精度偏差导致质量块零点偏移进而导致的非线性问题。文献[1]开展了高阶ΣΔ加速度传感器的非线性研究,研究了敏感结构非线性、运放非线性增益、静电力反馈非线性对系统的影响。由于没有考虑其他非线性因素,文献[1]中在大信号输入下积分器和敏感结构非线性行为级仿真显示谐波失真淹没在噪声中,而静电力反馈非线性谐波失真较大。实际上在加速度传感器应用中,往往输入加速度信号较大,在这种情况下接口电路的积分器建立、开关导通电阻、沟道电荷注入效应等都会产生非线性,这些非线性的建立和转换过程会在输出呈现出较大的谐波失真,从而影响带宽内有用信号精度。本文基于一种五阶ΣΔ加速度计闭环系统,分析了其各个主要部分的非线性,在MATLAB的Simulink下建立了非线性模型进行仿真。设计了一种单端五阶开关电容ΣΔ加速度计闭环接口电路,对比行为级仿真结果和电路仿真结果,验证了建立的模型的有效性。
1 主要非线性特性分析
1.1 敏感结构引起的电荷转换非线性

当传感器感知外界加速度ain时,质量块产生位移x,从而引起了差动电容值发生相反的变化,假如初始电容为C0,电容初始间距为d0,如果采用图1所示的开关电容检测方法对差动电容变化进行检测,则:

其中A0=2C0Vd/Cf,Vd是参考电压。当给系统施加较大的加速度信号时,质量块位移量x也较大,此时电荷转换输出电压的三次谐波分量不可忽略。基于MATLAB/Simulink下的函数可以很容易地建立该非线性模型。
1.2 积分器非线性
积分器是ΣΔ加速度计系统中的重要部分,主要非线性部分来源于非线性的直流增益、有限增益带宽、有限压摆率等。图2是开关电容积分器的积分模型图。如果运放摆率足够大,或者输入信号较小时,积分过程的非线性主要由积分器中的运放非线性增益引起,关于运放的非线性直流增益模型已经在文献[1]中给出。然而当考虑到低功耗设计或者输入信号较大时,运放的有限压摆率和带宽将会导致积分器的建立非线性。此时有|Va(0+)|>Io/gm, 积分器输出为:


从式(2)可以看出,当积分器的输入信号增大,由运放摆率和带宽限制的非线性部分开始占据主要部分。
1.3 开关非线性
用开关电容电路来实现ΣΔ加速度计接口电路时,模拟开关的大量使用会引入开关的非线性问题。开关在导通时处于线性工作区,一般情况下采用CMOS互补开关,则开关导通电阻为:

其中r1~r3是关于工艺和电容的系数。由上式可以看出由开关导通电阻导致的积分器输出非线性。其本质上是由衬底偏置效应引起的。同理,衬底偏置效应也会引起沟道电荷注入过程中的非线性,导致谐波失真的产生,这些非线性的关系式可以很容易地在MATLAB中建立模型。

静电力反馈非线性和运放直流增益非线性已经在文献[1]中给出,这里不再详细描述,只在系统建模中加入其非线性模型,建立完备的整体ΣΔ加速度计非线性模型。另外为了系统建模时的准确性,在系统模型中加入开关采样抖动、kT/C噪声、运放噪声等等非理想特性,结合上文所描述的开关非线性、C-V转换非线性、积分器非线性、静电力反馈非线性模块,建立的非理想特性五阶加速度计系统模型如图3所示。该五阶加速度计结构参考了文献[3]的结构,本文的加速度计系统基于一种低Q值传感器表头,该高阶结构的稳定性是基于后级电学调制器局部反馈系数的调整。当采样频率为250 kHz,输入信号244.12 Hz,信号幅度为0.3 g时,行为级非理想模型仿真结果如图4所示,系统输出噪底的平均值约为-150 dB,三次谐波失真约为-103.9 dB。

2 电路设计和版图后仿真
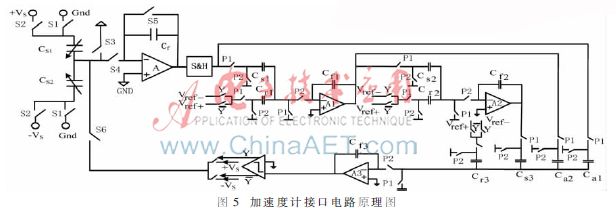
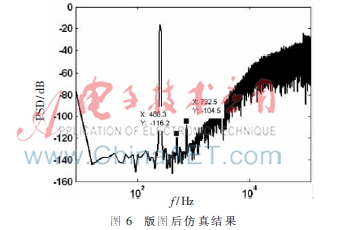
图5是本文设计的加速度计接口电路原理图。图中包含了等效的机械结构部分(可变电容Cs1和Cs2)、前级低噪声电荷敏感电路、采样保持电路(S&H)、积分器网络以及比较器电路。该设计的前级低噪声检测电路参考了文献[1]的设计思路,实现高精度的电荷转换输出。后级三阶积分器网络和两阶加速度计表头构成了五阶的高阶系统,抑制了系统的量化噪声。积分器网络中的采样电容和反馈电容分离,这样能够很方便地实现局部反馈因子,使得反馈参考电压能够一致,不用分别设计参考电压值。该结构采用一位量化输出,所以比较器的输出可以直接用来控制一位DAC反馈的开关,将数字输出转换成模拟参考信号,反馈给加速度计表头。在TSMC 0.35 ?滋m工艺下对该单端加速度计接口电路进行版图设计和优化,将该接口电路的版图网表导入Spectre下进行后仿真,采样频率为250 kHz,输入正弦信号同样为244.12 Hz,信号幅度为0.3 g,版图的后仿真结果如图6所示,系统输出噪底的平均值约为-140 dB,比行为级仿真结果高了约10 dB,这可能是前级电荷检测部分的噪声混叠导致的。版图后仿真的二次谐波失真为-116.2 dB,三次谐波失真为-104.5 dB。二次谐波的产生是由于本文为了简化设计流程,采用了单端实现的方式。在版图设计时由于工艺参数的误差,都会使得设计值和理想的参数存在一定的偏差。后仿真结果的三次谐波失真和行为级结果差别不大,这从一个方面反映了行为级非线性模型的准确性。另外版图后仿真结果显示其和行为级模型有一样的噪声整形能力,这说明了电路设计的正确性。
3 结束语
本文分析了ΣΔ加速度计系统的非线性,并在MATLAB中建立了一个五阶加速度计系统的整体模型,其中包含了主要的非线性模型和噪声特性模型,利用根轨迹法分析了高阶系统的稳定性。在TSMC 0.35 ?滋m工艺下实现了加速度计接口电路和版图设计,版图的后仿真结果显示当输入0.3 g的正弦加速度信号时,输出的三次谐波失真和行为级建模基本一致,由于噪声混叠使得输出噪底比行为级提高了10 dB。后仿真结果表明设计的电路和行为级模型具有一样的噪声整形能力,进一步验证了建立的行为级模型的准确性和电路实现的正确性。
参考文献
[1] 吕炳均.高阶SIGMA DELTA微加速度计接口ASIC芯片研究[D].哈尔滨:哈尔滨工业大学,2013.
[2] Xiao Dingbang,Wu Xuezhong,Li Shengyi.System design of second-order sigma delta micromachined accelerometer[C].Proceedings of the 1st IEEE International Conference on Nano/Micro Engineered and Molecular Systems,2006:299-302.
[3] LIU X W,XU H L,Yin L,et al.A low noise sigma-delta microaccelerometer interface circuit[J].IEICE Electronics Express,2014,11(12):1-6.
[4] 刘云涛.电容式SIGMA-DELTA微加速度计接口ASIC芯片研究[D].哈尔滨:哈尔滨工业大学,2010.
[5] 孙腾,车录锋,黎晓林,等.基于PID反馈的高Q值加速度计闭环检测电路[J].传感器与微系统,2011,30(2):101-106.
[6] Wan Caixin,Dong Jingxin.Nonlinearity of a closed-loop micro-accelerometer[C].16th IEEE International Conference on Control Applications,October 2007:1260-1265.
[7] 杨骁.宽带Sigma-Delta调制器的研究与设计[D].西安:西安交通大学,2008.

