李吉朝1,张海英1,王惠琴2
(1.西安理工大学 复杂系统控制与智能信息处理重点实验室,陕西 西安 710048;2.西安市环境监测站,陕西 西安 710048)
摘要:BP神经网络具有较强的学习能力,但在传统的研究中,隐含层节点、学习因子和动量因子往往采用试凑法得到相对较佳值,而试凑法在浪费较多时间的同时,可能得不到理想的BP神经网络输出,这对研究造成了一定的困难。文中采用智能算法来解决BP神经网络优化问题。遗传算法作为一种随机搜索算法,能够快速寻找到全局最优解,可以应用于本优化问题。因此,文章采用遗传算法优化BP神经网络上述参数,将改进后的BP神经网络运用于动力配煤非线性模型的研究。结果表明,采用遗传算法优化的BP神经网络具有较强的预测能力,对煤质的发热量预测误差优于线性平均模型误差,并且仿真表明动力配煤模型为近似线性的非线性模型, BP网络的输出值误差波动较小,结果理想。
关键词:动力配煤;BP神经网络;遗传算法;非线性
中图分类号:TP181文献标识码:ADOI: 10.19358/j.issn.1674-7720.2017.09.018
引用格式:李吉朝,张海英,王惠琴.基于遗传算法的BP神经网络优化动力配煤模型的研究[J].微型机与应用,2017,36(9):60-63,66.
0引言
动力配煤,顾名思义是将两种及两种以上的单煤混合成新的煤种。动力配煤有着其必要性,首先,发电系统锅炉都有其对应的设计煤种,往往由于煤种分布、资源短缺等一些客观因素,热电厂只能选择综合性价比相对较高的单煤混烧,这对锅炉的安全稳定运行带来一定的影响;其次,当前环境问题愈发严重,我国热力发电企业占发电行业70%左右,煤的大量使用对环境造成严重污染,因此,硫的排放被国家列为强制性指标。动力配煤技术可以利用某一种煤或几种煤的长处弥补另一种或几种煤的不足,取长补短,达到使锅炉用煤的品质稳定,解决煤质与炉型不相匹配的矛盾,使节能减排效益最大化[1]。
国内外研究表明,动力配煤模型分为线性模型[24]与非线性模型[5],目标函数为经济性目标,即混煤的总金额最小,约束条件包含多种变量,包括发热量、硫分、挥发分、灰分等。线性模型与非线性模型的判断在于约束条件的选取,对于模型的讨论,争议不断。近几年,浙江大学热工院进行过研究,得出的结论是混煤的参数模型是一个近似线性的非线性模型。但是,对于煤的一些重要参数,比如发热量,浙江大学热工院的混煤实测值与线性加权平均值存在5%左右的误差,这个误差相对来说比较大,因此,动力配煤非线性模型的研究具有现实意义。
本研究项目来自于西安某热电厂,电厂来煤分为高热低硫、中热中硫、低热高硫三大类煤,存储在3个煤场中,入炉煤是将这三类煤进行掺烧。

1BP神经网络的研究[6 8]
动力配煤的性能指标包括发热量、硫分、挥发分、水份、灰分等。其中发热量对锅炉安全稳定运行影响较大,硫分对环境的影响较大,本研究重点考虑这两个性能指标,以经济为主要目标,锅炉安全性以及环保性为约束条件,得到的动力配煤数学模型[9]如下:
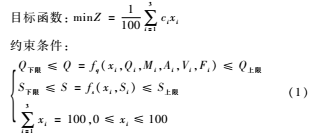
其中,目标函数中Z为混煤的平均价格,ci为单煤的单价,xi为单煤的配比,约束条件中Q为煤的发热量,其影响因素依次为单煤的配比xi、单煤的发热量Qi、单煤的水份Mi、单煤的灰分Ai、单煤的挥发分Vi以及单煤的固定碳Fi,约束条件中S表示煤的硫分,其影响因素依次为单煤的配比xi、单煤的硫分Si。
由动力配煤模型可知,动力配煤的约束条件为非线性,需要应用学习算法得到其模型,本研究以发热量为例,3种煤混配输出影响参数有18个,分别为3种单煤对应的配比、发热量、水份、灰分、挥发分以及固定碳。因此,BP神经网络[10-13]的输入点为18个,输出点为1个。3层BP神经网络隐含层输入点数的计算公式如下:
n=p+q+a(2)
其中,p为输入层的神经元个数,q为输出层神经元个数,a的取值范围为0~10之间的整数。
由于BP神经网络存在两大问题,收敛速度慢及容易陷入局部最优。为了解决上面两个问题,在标准BP神经网络的基础上引进动量项,公式如下:
w(k+1)=w(k)+α[(1-η)D(k)+ηD(k-1)](3)
其中,η为学习因子,取值范围为0.01~1;α为动量因子,取值范围为0~1。学习因子是影响BP神经网络收敛速度的关键因素之一,如果学习因子太小,网络的收敛速度会非常缓慢;如果学习因子太大,又会使网络出现振荡而无法收敛。
加入动量项的本质是使得学习过程中的学习因子η不再是一个恒定的值,而是可以不断变化。通常来说,动量因子不易过大,如果动量因子太大,动量项所占的比例过重,则本次误差修正项的作用会削弱太多,以致完全不起作用,反而会延长收敛时间,甚至会引起振荡。一般情况下,动量系数的最大值在0.9左右。
在以往的BP学习过程中,往往通过经验来选取隐含层节点数、学习因子以及动量因子,使得BP神经网络达不到最佳性能,因此,本研究运用遗传算法[1418]对上述3个参数进行优化,目标函数为BP神经网络的输出误差。图1为遗传算法优化BP神经网网络流程图。
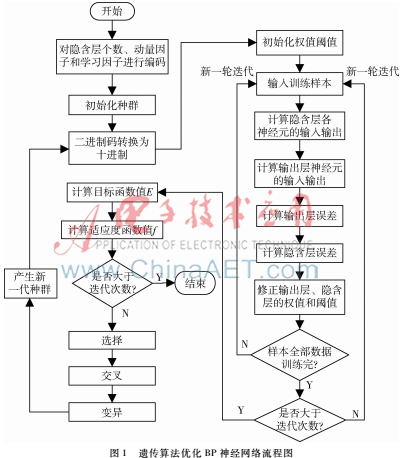
2种群的编码
本研究种群编码采用二进制编码,将隐含层节点、学习因子以及动量因子串成一个字符串,其中隐含层节点范围为0~14,学习因子以及动量因子的范围均为0~100,初始种群数目为20个。隐含层节点为4位二进制数,学习因子为7位二进制数,动量因子为7位二进制数,因此二进制编码为18位。如果参数a的变化范围为[amin,amax],用m位二进制数b来表示,则二者之间满足:
a=amin+b2m-1(amax-amin)(4)
由于隐含层节点必须为大于0的整数,因此这里需要对其向上取整。
3目标函数值计算
将BP神经网络改写成function函数,形式如下:
E=mubiao(a,b,c)(5)
其中a为隐含层节点数,b为学习因子,c为动量因子,E为网络输出的总误差,即为遗传算法的目标函数,这里的E越小,网络越好。
4适应度函数的选择
目标函数是极小值,那么对于适应度的函数有下面两种表示方法:

第一种方法由于E数值过小,得到的差值f1基本相同,所以不适用,因此选择第二种适应度计算公式,不过进行了改进,由于E的数值为10-3级,先对目标函数值归一化处理,处理公式如下:

经过归一化处理的目标函数分布在0~1范围内,接下来对归一化后的目标函数放大到0~100范围内,放大函数为:

所求得f即为适应度值。选择轮盘赌法,适应值越大,被选择的概率越高。选择概率计算公式为:
pi=fi∑ni=1fi(9)
5仿真结果
实验研究发现,网络输出的值均匀分布在实测值的两端,并且具有较好的预测能力。遗传算法寻优得到的隐含层节点为6个,学习因子为0.3,动量因子为0.1。
本文中所采用数据来自于参考文献[9],每3种煤按特定比例掺配,总共有48个样本,网络输入层为18个节点,输出层为1个节点,将3种煤的顺序调换可以扩展为288个样本,由于学习样本数量有限,并且BP神经网络学习预测能力的强弱取决于学习样本的数量,因此本文将288个样本绝大多数作为学习样本,少量作为预测样本,并且学习样本做到包含全部配比信息。分别按照学习样本与预测样本之比为240∶48、252∶36、264∶24做了3次仿真,其统计结果如表1所示。
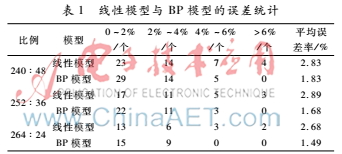
仿真图选取的配比为262∶24,仿真结果如图2~图6所示。
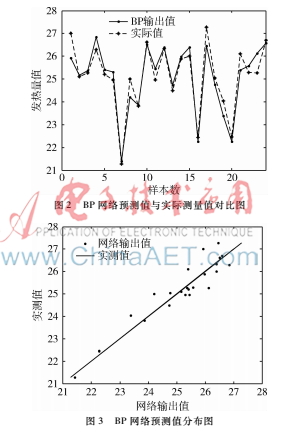


图2中,经过遗传算法优化参数之后的BP神经网络具有较强的预测能力,BP网络输出值能够较好地跟随实测值上下波动,因此为单煤掺配后热值具有非线性提供了较好的依据。
图3中,可以看出网络输出值分布在实测值附近,偏离较小,网络预测能力较强。
图4中,线性平均值也能够较好地逼近实测值,但是存在少量误差较大的点,其逼近效果较网络预测差。
图5中,线性平均值散落在实测值附近,可以明显看出线性平均值比网络预测值差。
从图6中可以看出,线性平均值与实测值误差率较大,并且存在较大的波动,BP输出值与实测值误差率相对较小,并且比较平稳。
6结束语
首先,遗传算法具有较强的寻优能力,但是对于目标函数的值较大,并且作为适应度时,对于遗传算法的收敛存在较大的影响,作为轮盘赌法,比如两个适应度值49 000与50 000,寻优过程中可能会错误地认为50 000为最小值,因为两者概率都比较接近50%,但是实验者可以判断出49 000为最小值。因此,在此基础上本文创新性地提出适应度归一化,放大两个相接近的较大适应度值之间的差距,提高淘汰率,并且加快收敛速度。
其次,依靠试凑法得到BP神经网络往往浪费时间,而且得不到理想模型。本文创新性地通过遗传算法优化BP神经网络的隐含层节点、学习因子和动量因子,使BP神经网络的预测能力达到相对最佳,减少依靠试凑法带来的随机性。实验表明,该方法得到的BP神经网络预测能力较强;动力配煤非线性模型与线性模型接近,但是,非线性模型的输出值与实测值的误差小于线性模型的输出与实测值的误差,并且误差更加平稳。因此,本文认为动力配煤模型为近似线性模型的非线性模型。
参考文献
[1] 屈国强.动力配煤优化研究现状及展望[J].洁净煤技术,2015,21(6):6-10,14.
[2] 谷丽景,李永华,李路.电站锅炉燃烧优化混合模型预测[J].中国电机工程学报,2015,35(9):2231-2237.
[3] 李彬,尉守科,于俊清,等.火电企业配煤模型与优化算法[J].计算机工程与设计,2015,36(9):2388-2394.
[4] 夏季,张成,袁向宇,等.基于物理规划的混煤掺烧方案优化模型[J].煤炭学报,2015,40(11):2654-2660.
[5] 陆潘. 烟煤掺烧印尼煤的动力配煤模型研究[D].武汉:华中科技大学,2011.
[6] 刘春艳,凌建春,寇林元,等.GABP神经网络与BP神经网络性能比较[J].中国卫生统计,2013,30(2):173-176,181.
[7] 黄忠棋.基于BP神经网络的墙地砖缺陷检测技术研究[J].微型机与应用,2014,33(23):81-83.
[8] 刘天舒.BP神经网络的改进研究及应用[D].哈尔滨:东北农业大学,2011.
[9] 李颖.基于非线性理论的动力配煤模型的研究[D].杭州:浙江大学,2002.
[10] Liao Yanfen, Wu Changhong, Ma Xiaoqian.New hybrid optimization model for power coal blending[C].International Conference on Machine Learning and Cybernetics. IEEE, Guangzhou, China, 2005(7):4023-4027.
[11] DESHPANDE P, WARKE N, KHANDARE P,et al.Thermal power plant analysis using artificial neural network[C].Nirma University International Conference on Engineering,2012:16.
[12] 李松,刘力军,解永乐.遗传算法优化BP神经网络的短时交通流混沌预测[J].控制与决策,2011,26(10):1581-1585.
[13] Cheng Jun, Wang Xin, Si Tingting, et al.Ignition temperature and activation energy of power coal blends predicted with backpropagation neural network models[J]. Fuel,2016,173(1):230-238.
[14] Hao Zhou, Qian Xinping, Cen Kefa, et al.Optimizing pulverized coal combustion performance based on ANN and GA[J]. Fuel Processing Technology, 2004, 85(23):113-124.
[15] 夏季,华志刚,彭鹏,等.基于非支配排序遗传算法的无约束多目标优化配煤模型[J].中国电机工程学报,2011,31(2):8590.
[16] 刘玉娇,张海英,关海盈.基于多种算法的多目标配煤优化方法[J].热力发电,2014,43(9):108-112.
[17] 燕礼富,邓全亮,范怿涛.基于预测模型和遗传算法的配煤优化研究[J].计算技术与自动化,2010,29(3):31-34.
[18] Guo Xijin, Chen Ming, Wu Jiawei.Coal blending optimization of coal preparation production process based on improved GA[J]. Procedia Earth and Planetary Science, 2009, 1(1):654-660.

