0 引言

　　微机电系统(Micro Electro Mechanical Systems，MEMS)陀螺仪已经广泛应用于惯性导航、组合导航系统中[1]。但是目前低成本MEMS陀螺仪精度相对较低，零偏稳定度等性能较差，而作为导航应用对MEMS陀螺仪的精度要求较高，因此，在使用前首先要对随机误差进行处理[1]。

　　处理这个问题的思路一般是首先建立输出的误差模型，再根据一定的滤波技术，通常是Kalman滤波[2]，或小波变换等滤波方法[3]来估计和补偿陀螺误差。以前的相关工作一般在对单一型号陀螺仪进行分析的基础上，建立AR模型来近似描述误差[3-5]，取得了一定的滤波效果。然而，低成本MEMS陀螺误差成分复杂，不同低成本MEMS陀螺之间一致性差，启动重复性差[6]。因此，难以对低成本MEMS陀螺建立准确的误差模型，对一个陀螺的建模也无法适用其他陀螺。

　　为解决对低成本MEMS陀螺建模困难的问题，本文从工程实际应用角度出发，使用Allan方差法分析了MEMS陀螺仪输出的特点，详细探讨了一种普遍适合低成本MEMS陀螺仪的实用随机误差实时处理方法。该方法由零偏补偿、可去除粗大误差的平均滤波算法和基于最小二乘法预测的Kalman滤波器三部分共同组成。其中，传统Kalman滤波算法需要建立误差模型以写出系统状态方程，本文所述方法不同于传统方法，可以不对误差进行建模，具有更好的通用性。实验结果证明，该方法可以有效滤除噪声，并具有良好动态特性。

1 基于Allan方差的陀螺误差分析

　　为获得低成本MEMS陀螺仪输出的误差特性，首先设计实验条件采集数据并保存，然后根据文献[7、8]中所描述的Allan方差分析法对数据进行分析。

　　1.1 数据采集

　　选取若干同一型号低成本MEMS三轴陀螺仪，该型号陀螺仪以数字量输出，AD位数为16位。在恒温并且将器件固定的条件下每一枚器件进行两次上电数据采集。每次上电首先预热30 min，然后保存数据。采样率设置为100 Hz，每次保存15 min数据。

　　1.2 使用Allan方差分析法分析数据

　　Allan方差分析法可以确定产生数据噪声的基本随机过程特性，并能识别给定噪声的来源[8]。Allan方差的计算公式为[7]：

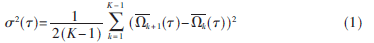
　　式中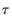，表示平均时间，K为所划分的子集个数，为第k个子集的平均值。按照式(1)计算每个平均时间的Allan方差，以双对数曲线画出Allan标准差随平均时间变化的情况。任选一个器件两次上电测试的原始数据，绘制双对数曲线，如图1所示。

　　选取器件的X轴，分别计算测试数据的均值和均方差，计算结果如表1所示。

　　利用文献[7]中所描述的分析方法对图1和表1进行分析可知，该型号陀螺仪输出随机漂移中，角度随机游走占据主要部分；同一器件不同测量轴误差特性各不相同；同一个陀螺仪两次上电的误差特性并不相同。

　　由于采用16位AD，原始输出序列的范围在-32 768～

　　32 768之间，通过观察，发现数据中偶尔存在一些明显错误的野值，例如，一段实测原始输出序列为67，49，

　　55，-233，21，17，23，63。可以发现，数据-233明显不合理，属于野值，这种野值一般不会在连续10个采样中出现两次。

2 实时滤波算法

　　由分析的结果可以发现难以建立一个通用的陀螺误差模型。因此，对误差建模的方法并不适用于低成本MEMS陀螺仪。针对低成本MEMS陀螺输出特点，本文设计了一种实时滤波算法，该方法分为三个步骤。

　　2.1 零偏补偿

　　在进行滤波之前，首先应该去除原始测量值中的常值漂移信号[1]。文献[1]指出，可以用一段零输入条件下输出数据的均值代表整体的零偏。经充分预热后，在敏感轴上零角速度输入，保存一定时间的数据。对这段数据求均值，作为陀螺仪输出的零偏，在以后每次得到的原始值都减去这个零偏。

　　2.2 平均滤波算法

　　对已去除零偏的原始数据，由于存在粗差，应先设法抑制。

　　首先，用陀螺仪以往的几个测量值的均值作为下一次实际值的估计[5]，均值估计法的表达式为：

　　式中，xi为数据窗内的元素，L为数据窗的长度，为均值估计结果。由于不是滑动平均方式，经过平均后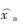，的输出率为xi输出率的1/L，L越大，输出率越低。

　　通过观察原始数据可以发现，野值一般不会在短期内连续出现，野值和正常值的偏差在200以上。因此，本文选取L=5，对5个历史数据平均得到估计结果，再设置一个门限值q，然后将5个历史数据xi分别和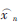做差，用差值的绝对值和q比较，如果大于q，则xi被判决为野值，否则为有效数据。实际使用时，L和q应根据需要灵活选取。最后，将剩下的有效数据xi再次用式(2)计算均值，作为平均滤波后的结果输出。经过平均滤波后的输出序列不仅消除了粗大误差的影响，方差也显著降低。

　　2.3 基于最小二乘法预测的Kalman滤波算法

　　在经过平均滤波算法后，将输出再经过Kalman滤波器进一步处理。

　　Kalman滤波是工程中应用的成熟方法，其工作过程可以分为预测和校正两个过程[9]。预测过程在上一个历元状态估计值的基础上，利用系统的状态方程来预测当前历元的状态值，即先验估计值。涉及公式如下：

　　校正过程利用实际测量值来校正经上一步预测得到的状态先验估计值，获得后验估计值。涉及公式如下：

　　对于预测过程，由于无法对低成本MEMS陀螺仪误差建立通用、准确的模型，不能采用传统的建立AR模型预测的方法，但并不意味着无法对当前输出值做出先验估计。载体运动具有连续性和运动变化的缓慢性[9]，这意味着载体具有保持原来运动状态的趋势，在短时间内的真实角速度不会发生突变。最小二乘法通过最小化误差的平方和寻找数据的最佳函数匹配，利用最小二乘法可以简便地根据历史记录数据估计下一时刻的真值，并使得估计数据和真实数据误差的平方和最小。

　　另外，最小二乘法直接根据历史后验估计值实时调整参数，来预测下一时刻的实际值，是一种动态的预测方法，这样不仅适用于静止条件下的滤波，在有角速度输入变化的情况下依然可以有效工作。

　　本文设置一个深度为10的FIFO，用于保存Kalman滤波后验估计值输出结果。FIFO内为按时间先后顺序排列的最近的10个滤波后输出结果。对于一般的应用场景，在短时内载体不可能发生剧烈的运动状态变化，数据序列具有稳定性，拟合的结果近似为一条直线。为保证预测准确性并兼顾计算复杂度，使用二次函数拟合，令：

　　式中，ti为时间序列；xi为对应的后验估计值，即实际使用值；a、b、c为拟合二次函数的参数，此时为未知。令：

　　其中，为利用式(8)计算得到的每一时刻的估计值，是未知参数的函数，分别与实际值作差。?追为这些差的平方和。根据最小二乘法原理，?追应取得最小值。用函数?追对a、b、c求偏导数，令偏导数等于0，获得关于a、b、c的线性方程组，解方程确定未知参数，代入式(8)，可得：

　　使用式(10)即可获得当前时刻的先验估计值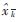，式(10)也即系统状态方程。另外，预测过程除了获得预测值，还需要一个衡量预测值可靠性的过程噪声参数Q。由于预测值将在校正过程中被校正，将校正后的使用值序列和预测值序列做差分，差分序列的方差即表示预测结果的可靠性。即：

　　对于校正过程，根据去除粗大误差后，由式(2)计算得到的平均滤波结果，作为校正过程的测量值输入。测量噪声R用平均滤波后的数据方差衡量，即：

　　调整合适的状态均方差初始估计值P0，保证滤波器收敛。以Kalman滤波后的校正值作为使用值输出，完成对陀螺输出的滤波。

3 滤波器性能测试

　　为不失一般性，再选一颗该型号MEMS陀螺仪的输出数据，使用上述滤波方法对数据进行实时处理。为描述动态下的滤波性能，可以使用在所采集的静态数据基础上叠加一个角速率来模拟动态变化[2]。

　　3.1 静态实验

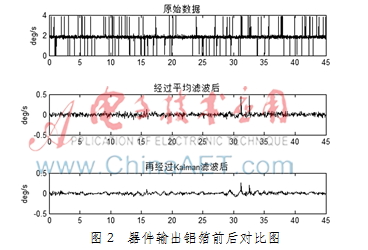
　　截取一段时间数据作图，图2展示陀螺滤波前后的输出对比。

　　由图2看出，虽然原始输出的零偏和波动性相差很大，图形上有较密集的毛刺，但是在经过常值漂移补偿，平均滤波算法后，输出零偏有效改善，毛刺被基本滤除，粗大误差得到了有效抑制。在此基础上，Kalman滤波器进一步改善了零偏稳定度，获得了更出色的滤波降噪效果。将这段数据的均值和均方差进行定量计算，如表2所示。

　　由表2看出，经过滤波，能使零偏减小到令人满意的程度，同时，均方差在滤波后小于滤波前的十分之一，证明输出序列的波动性被显著降低，零偏稳定度性能得到大幅提升。

　　3.2 动态实验

　　选取另一颗陀螺仪采样，首先截取90 s静态实验数据，以一次函数拟合模拟匀角加速度转动过程；以常数模拟匀角速度转动；以正弦函数模拟较为复杂角速度变化情况。图3为模拟信号、与原始数据叠加后信号和滤波后信号对比图。

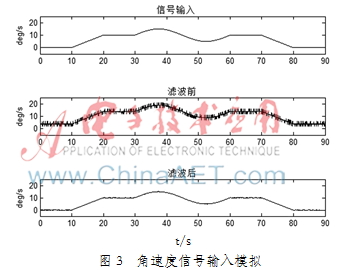
　　由图3看出，滤波后，零偏被有效校正，方差明显降低，输出较完美地恢复了输入信号，证明该方法在动态下依然可以有效工作，工程实际应用价值较高。

4 结论

　　低成本MEMS陀螺仪特性参差不齐，启动重复性差，不适宜采用对误差建模的方法处理随机误差。本文所述实时滤波算法从实际工程应用角度出发，可以较好地抑制低成本MEMS陀螺随机误差中的角度随机游走，有效补偿常值漂移，均方差小于滤波前的十分之一，大幅提升低成本MEMS陀螺仪零偏稳定度性能。该方法不仅能在静态下工作，在动态情况下不会淹没有效信号，也表现出良好性能。另外，该方法相对易于实现，算法复杂度相对低，普遍适用于低成本MEMS陀螺仪的随机误差滤波，具有较高的实用价值。

参考文献

　　[1] 蒙涛，王昊，李辉，等.MEMS陀螺误差建模与滤波方法[J].系统工程与电子技术，2009，31(8)：1944-1948.

　　[2] 钱华明，夏全喜，阙兴涛，等.基于Kalman滤波的MEMS陀螺仪滤波算法[J].哈尔滨工程大学学报，2010，31(9)：1217-1221.

　　[3] 丛丽，秦红磊，邢菊红.小波阈值去噪和FAR建模结合的MEMS陀螺数据处理方法[J].电子技术应用，2010，36(12)：120-123.

　　[4] 陈涛，王新龙，杜宇.基于AR模型的光纤陀螺建模方法研究[J].鱼雷技术，2005，13(3)：25-27.

　　[5] 吉训生，王寿荣.MEMS陀螺仪随机漂移误差研究[J].宇航学报，2006，27(4)：640-642.

　　[6] 张智永，周晓尧，范大鹏.稳定平台中陀螺漂移自适应实时估计算法[J].航空学报，2012，33(6)：1044-1051.

　　[7] 赵思浩，陆明泉，冯振明.MEMS惯性器件误差系数的Allan方差分析方法[J].中国科学，2010，40(5)：672-675.

　　[8] 王新龙，李娜.MEMS陀螺随机误差的建模与分析[J].北京航空航天大学学报，2012，38(2)：170-174.

　　[9] 谢钢.GPS原理与接收机设计[M].北京：电子工业出版社，2009：129-134.