0 引言

    Ahlswede于2000年提出网络编码(Network Coding，NC)的概念^[1]，其主要思想即中继节点对源节点发送来的信息进行编码映射等操作后再进行转发。基于充分利用无线通信中叠加电磁波的目的，Zhang于2006年提出物理层网络编码(Physical Layer Network Coding，PNC)^[2]，物理层网络编码与传统传输模式相比，信息交换时隙减少一半，网络吞吐量提高一倍，但是误码率有所上升。

    为提高物理层网络编码传输的可靠性，许多学者通过信道编码与物理层网络编码的联合设计降低通信误码率。Maria提出一种Turbo码与物理层网络编码联合设计的方案(PNC-Turbo)^[3]，该方案在中继节点对叠加和信号进行软处理，与未进行联合设计时相比有4.5 dB的性能增益。需要注意的是，PNC-Turbo机制是目前能发现的物理层网络编码设计中误比特性能最好的，但是Turbo码的译码器复杂度较高。Li等采用Exit分析法，将低密度奇偶校验码(LDPC)和物理层网络编码联合设计(PNC-LDPC)^[4]，与LDPC码和网络编码联合设计方案相比，提出方案有0.8 dB的性能增益，并且提高了信道容量。Chen等基于比特交织编码调制(BICM)提出一种编码调制(Coded Modulation，CM)技术与物理层网络编码的联合实施机制(PNC-BICM)^[5]，通过将物理层网络编码、信道编码与调制三者联合设计，分析同步和异步条件下通信系统性能，证明了该联合机制的优越性。

    PNC-BICM在Rayleigh信道中具有良好的性能，但是在AWGN信道中，随机交织器的存在造成欧氏距离减小，使得系统可靠性下降。为进一步降低误比特率，PNC-BICM-ID通过迭代技术使同一编码单元中的各个码元之间彼此独立，增大信号点之间的自由距离，提高大信噪比(Signal to Noise，SNR)下的系统可靠性。PNC-Turbo具有优异的性能，但是由于译码时采用两个SISO(soft-input soft-output)译码模块，译码复杂度较高，为减小译码复杂度，本文提出的PNC-BICM-ID仅采用一个SISO译码模块，译码复杂度是PNC-Turbo的一半。

1 系统模型

    本文使用双向中继信道模型(Two Way Relay Channel)^[6]，时隙控制协议为两时隙不含直接链路传输^[7]，如图1所示。节点A和节点B是端节点，节点R是中继节点，由于A和B的距离超出可靠通信距离，A和B只能通过R进行信息交换。假定系统中所有节点工作在时分半双工通信模式下，系统完全同步，信号发射功率相等，两个源节点到中继节点的距离相等，信道为加性高斯白噪声信道，噪声均值为0，噪声方差为?滓2，双边功率谱密度为N₀/2。

2 基于BICM-ID的信道编码与PNC的联合设计

    研究表明，BICM-ID的传输可靠性超过了传统的TCM和BICM等信道编码方法，其计算复杂度较低，在AWGN和Rayleigh信道下具有良好的性能^[8]。本文所提方案是基于BICM-ID的PNC与CM的联合机制。

2.1 PNC-BICM-ID设计

    假设节点A和节点B采用相同的编码调制方式。BICM-ID的编码器选择十分灵活，因为卷积码编译码结构简单、延时小、应用广泛，本文编码器采用卷积编码。交织器采用伪随机交织器，由带线性反馈的移位寄存器生成，打乱编码序列中的信息位顺序，降低序列之间的相关性。调制方式采用QPSK调制。

    如图2所示，在多址接入阶段，节点A(B)将信源编码后二进制比特序列b_A(b_B)通过卷积码编码器生成二进制编码比特序列c_A(c_B)，通过伪随机交织器输出x_A(x_B)，通过QPSK调制器生成信息s_A(s_B)，并将其发送到中继节点R。中继节点接收到的信号为：

    在广播阶段，节点R将yR解调、解交织、译码生成广播信息s_R，该过程采用软信息迭代反馈，从而提高译码性能。节点A(B)接收到sR后可利用自身缓存的信息以及接收到的广播信息通过异或运算得到节点B(A)的信息。

2.2 映射规则设计

    根据中继比特的判决结果，基于PNC的特点，将y_R映射成图3中对应的九个星座点，其中E_S为信号能量。

2.3 译码算法设计

    BICM-ID一个鲜明的特点是存在低复杂度的译码算法。本文采用SISO译码模块，如图4所示。中继节点接收到多址接入信息后，具体译码过程如下：

    (1)解调器根据多址接入信息和先验信息产生解调信息D₁。先验信息A₁=ln(P(y_R=1)/P(y_R=0))，假设发送先验概率相等，则首次迭代时A₁=0。

    (2)根据解调信息D₁和先验信息A₁生成外附信息E₁，送入解交织器。解交织器产生先验信息A₂，并送入MAP译码器。

    (3)MAP译码器产生译码信息D₂，广播到目的节点，同时根据译码信息D₂和先验信息A₂生成外附信息E₂，送入交织器产生先验信息A₁，进行迭代。

    其中，A₁、A₂、E₁、E₂、D₁、D₂都是对数似然比值，且E₁=D₁-A₁，E₂=D₂-A₂。

3 误比特率性能分析

    由于PNC-BICM-ID中伪随机交织器和卷积码的存在，在理论上给出确定的误比特率解析式十分困难，此处基于BICM系统的经典性能界进行推导。

    BICM系统中码率为k/n的分组码误比特率的联合限为^[9]：

其中，W₁(d)是所有错误图样中汉明距离为d的码字数量，d_min是码字的最小汉明距离，f(d，m，c)为成对错误概率(Pairwise Error Probability，PEP)的密度函数，其参数分别为汉明距离d、映射图样m、信号星座集c。f(d，m，c)可由下式表示：

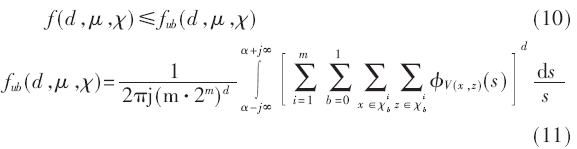
式中，f_ub(d，m，c)为联合界，V(x，z)=log p(y|x)-log p(y|z)，φ_V(x，z)为V(x，z)的Laplace变换，a为Laplace展开式常量，m为每个符号序列包含的比特数，b为信息符号集且为信息符号子集，x为信号点，z为星座点。

    BICM-ID系统在低误比特率时将收敛到错误平层(Error Floor Bound，EF Bound)，此时PEP由下式表示：

4 仿真试验

    仿真试验条件：信道为AWGN信道，系统中所有节点工作在时分半双工通信模式下，系统完全同步，信号发射功率相等。卷积编码器码元长度为2 304，码率R_C=1/2，约束长度L=5。调制方式为QPSK调制。

    仿真包含方案：本文提出的PNC-BICM-ID机制、PNC-Turbo机制、PNC-BICM机制。图5给出了不同信噪比下各个设计机制的误比特率。为了便于对比，各个设计机制的数据包长度均为2 304 bit。

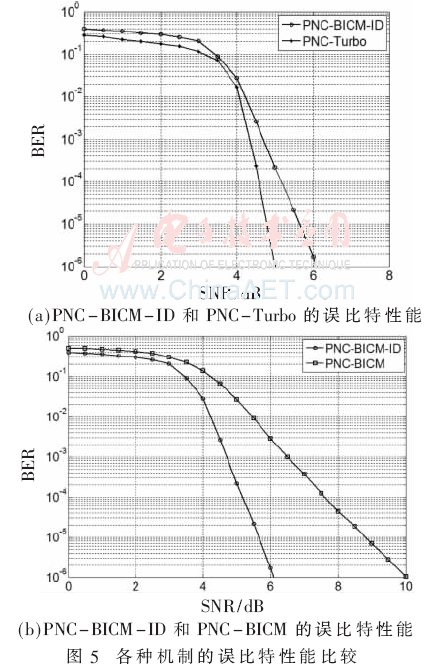
    图5(a)中，横坐标表示信噪比，其范围为[0，8]dB；纵坐标表示误比特率，其范围为[10^-6，10⁰]。图中的两条曲线是在仿真条件下误比特率随信噪比的变化曲线。从图中可以得知，两条曲线在低信噪比时基本重合；在高信噪比时相比PNC-Turbo机制，本文机制的误比特性能相差1 dB左右。由此表明，本文机制只采用一个SISO译码器，误比特率性能有所下降，但是差距不大，同时本文机制的译码复杂度降低了50%，更利于工程实现。

    图5(b)中，横坐标表示信噪比，其范围为[0，10]dB，纵坐标表示误比特率，其范围为[10^-6，10⁰]。图中的两条曲线是在仿真条件下误比特率随信噪比的变化曲线。从图中可以得知，两条曲线在低信噪比时误比特率性能差距不大，在高信噪比时相比PNC-BICM机制，本文机制的误比特性能提高了4 dB左右。表明本文机制采用迭代技术，误比特率明显降低，提高了编码增益，更适用于高斯信道。

5 结论

    本文提出了一种基于BICM-ID的编码调制技术和物理层网络编码联合设计的方案，该方案将信道编码、调制和物理层网络编码三者统一考虑，设计中继节点映射方案，增大欧式距离，降低通信传输误码率。同时，利用BICM-ID系统设计灵活的特点和卷积码编译码结构简单的性质，减小了系统译码复杂度。从仿真结果看，PNC-BICM-ID通过迭代译码提高了系统性能。总之，本文将BICM-ID和PNC联合设计，既降低了系统的误码率，又减小了系统译码复杂度。

参考文献

[1] AHLSWEDE R，CAI N，LI S Y R，et al.Network information flow[J].IEEE Transaction on Information Theory，2000，46(4)：1204-1216.

[2] ZHANG S，LIEW S C，LAM P P.Hot topic：physical-layer network coding[C].ACM MobiCom′06，Calfomia，2006：358-365.

[3] Maria Claudia Catro，Bartolomeu F.Uchoa-Filho.Improved joint turbo decoding and physical-layer network coding[C].IEEE ITW 2012，Lausanne，2012：742-746.

[4] Li Jun，Chen Wen，Lin Zihuai，et al.Design of physical layer network coded LDPC code for a multiple-access relaying system[J].IEEE Communications Letters，2013，17(4)：749-752.

[5] Chen Zhiyong，Xia Bin，Hu Zixia，et al.Design and analysis of multi-level physical-layer network coding for gaussian two-way relay channels[J].IEEE Transactions on Communications，2014，62(6)：1803-1817.

[6] VAZE R，HEATH R.On the capacity and diversity-multiplexing tradeoff of the two-way relay channel[J].IEEE Transactions on Information Theory，2011，57(7)：4219-4234.

[7] KIM S J，MITRAN P，TAROKH V.Performance bounds for bi-directional coded cooperation protocols[J].IEEE Transactions on Information Theory，2008，54(11)：5235-5241.

[8] LI X，RITCEY J A.Bit-interleaved coded modulation with iterative decoding using soft feedback[J].Electronics Letters，1998，34(10)：942-943.

[9] Guillen i Fabregas A，Martinez A，Caire G.Bit-interleaved coded modulation[J].Foundations and Trends in Communications and Information Theory，2008，5(1-2)：1-135.